What will you learn?
- You will learn how to obtain mathematical model representations (state-space representation and transfer-function representation) of linear systems in Scilab.
- You will learn how to transform the system model from transfer-function model to space-state model and vice versa.
What will you need?
- You need to have installed Scilab in your computer. I'm gonna use 5.5.2 version.
- Basic modern control theory knowledge.
- Programming knowlegde.
Difficulty
- Basic
In this tutorial we're gonna take an example of a linear system and define both its state-space representation and transfer-function representation with the syslin command, in order to we'll be able to take each representation of the system from one model to another. First we'll begin with transformation from state-space representation to transfer-function representation by using the ss2tf command. Then, we'll do the inverse procedure by taking the transfer-function representation to get state-space representation using the tf2ss command.
Important to remember that exist infinite state-space representations for a same system, Scilab gives you just one of them. We emphasize system models with multiple inputs and multiple outputs. Let's begin!
- Defining a Linear System in Scilab.
Before making any conversion first we shall define our system in Scilab in order to work with it.
Scilab let us define state-space representation of a system by supplying the main information (Time domain, A, B, C, D and initial state vector) to the `` `syslin``` command which returns a syslin list. Its syntax:
[system1]= syslin(dom,A,B,C [,D [,x0] ])
-system1 comes to represent the system below . You will notice that many functions related to control systems models receive a syslin list as input.
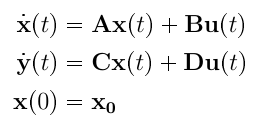
- Conversion
Now let's convert the system shown below , which has multiple inputs and multiple outputs and is defined by its state-space representation, into transfer-function representation.

We're gonna use the ss2tf command.
[TrF]=ss2tf(sl)
[D, NUM, DEM, Ft]=ss2tf(sl)
This command recieves a syslin list (linear system) and, called with one output it, returns the transfer matrix in TrF whose elements are transfer functions corresponding to possible combinations
of inputs and outputs. We expect in this example a 4x4 transfer matrix since we have two inputs and two outputs. By the other hand, if we call ss2tf with three outputs it returns the numerator polynomial matrix in NUM, the characteristic polynomial matrix in DEM and the feedthrough matrix in Ft.
//Enter the values of A, B, C, D
A=[0 1; -25 -4];
B=[1 1;0 1];
C=diag([1,1]); //Diagonal Matrix
D=diag([0,0]);
//Define the state-space representation
[SSsys]= syslin([],A,B,C,D); //dom may be 'c' for ,' d', [] or scalar
//Conversion
TFsys= ss2tf(SSsys); // Call ss2tf with one output
//or
[d, num, dem ]= ss2tf(SSsys); // Call ss2tf with three outputs
disp("Transfer-Function Representation:")
disp(TFsys)
disp("Numerator polynomial matrix:")
disp(num)
disp("Characteristic polynomial matrix")
disp(dem)
disp("Feedthrough polynomial matrix")
disp(d)
Now your variable browser should looks like this

After executing:

Now we're gonna use tf2ss command to do the conversion.
sl=tf2ss(TFsys)
It recieves a rational matrix TFsys, just like we obtained by using the ss2tfcommand, and returns a syslin list sl, i.e. , a state-space representation of our linear system. Thus, first we shall to know how to define a rational matrix whose elements are the transfer functions of our system.
- Defining a rational matrix.
The procedure is quite easy since we just have to declare a polynomial matrix. We 're gonna use the poly command to define polynomials with symbol 's' in this manner:
s=poly(0, 's')
Then, we will can define polynomials in order to build the rational matrix.
- Conversion
Let's transform from transfer-function representation to space-state representation the system we've been handling so far. So, first we enter the transfer functions and then we'll do the conversion.
clear
s=poly(0,'s') // Define the independent variable with symbol 's'
Cpoly=s^2+4*s+25; //Characteristic polynomial
Num=[(s+4) s+5 ; -25 s-25]; //Transfer functions numerator
TFsys=Num/Cpoly; //Transfer Functions
disp("Rational Matrix")
disp(TFsys)
SSsys=tf2ss(TFsys); //Conversion
disp("Space-State Rep")
disp("A=")
disp(SSsys(2));
disp("B")
disp(SSsys(3));
disp("C")
disp(SSsys(4));
disp("D")
disp(SSsys(5));
This is how your console should look after running.

Note that matrix A, B, C does not equal matrix A, B, C from our starting example, this is due there are infinitely state-space representations for a same system and Scilab just gave us one of them.
Thank you for reading! I hope this post will be helpful.
Posted on Utopian.io - Rewarding Open Source Contributors
Thank you for the contribution. It has been approved.
You can contact us on Discord.
[utopian-moderator]
Thank you! @roj
Hey @miguelangel2801 I am @utopian-io. I have just upvoted you!
Achievements
Suggestions
Get Noticed!
Community-Driven Witness!
I am the first and only Steem Community-Driven Witness. Participate on Discord. Lets GROW TOGETHER!
Up-vote this comment to grow my power and help Open Source contributions like this one. Want to chat? Join me on Discord https://discord.gg/Pc8HG9x