Repository
https://github.com/ajayyy/SponsorBlock
https://github.com/ajayyy/SponsorBlockServer
Voting
A very important feature to make this crowd-sourced system work and prevent bad actors is to implement voting.
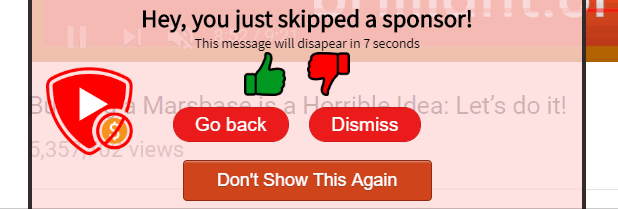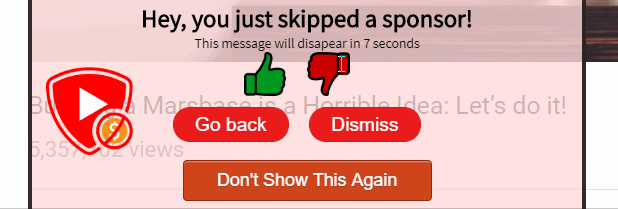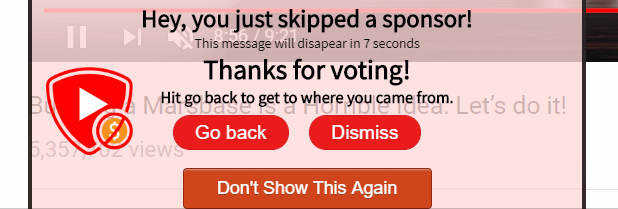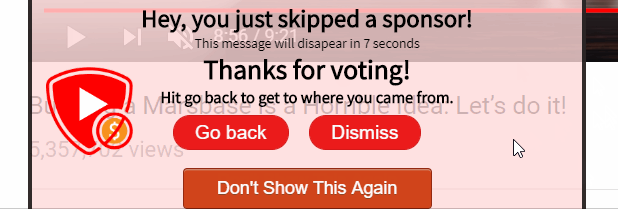
"Similar Sponsors"
A sponsor message at the beginning of the video shouldn't compete with one at the end of a video. To make votes matter, but not matter in some cases, the program tries to find "similar sponsors". Similar sponsors are sponsor times that are contained inside of each other.
//list of sponsors that are contained inside eachother
let similarSponsors = [];
for (let i = 0; i < sponsorTimes.length; i++) {
//see if the start time is located between the start and end time of the other sponsor time.
for (let j = 0; j < sponsorTimes.length; j++) {
if (sponsorTimes[j][0] > sponsorTimes[i][0] && sponsorTimes[j][0] < sponsorTimes[i][1]) {
//sponsor j is contained in sponsor i
similarSponsors.push([i, j]);
}
}
}
These sponsors then are compared for votes, and only the best one is sent to the user.
But it can't be that simple
In a system like that, one sponsor would get a few votes, and then the rest of the sponsors would never appear again, and could never get votes. I decided on using a more fancy algorithm that used a weighted random distribution based on a formula.
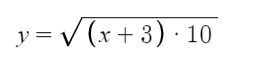
This formula makes small amount of votes (under 10), matter a lot, and makes the really large votes slowly not matter as much. This makes a newly submitted sponsor time always possible to be sent out to users to get votes.
let similarSponsorsGroups = [];
//once they have been added to a group, they don't need to be dealt with anymore
let dealtWithSimilarSponsors = [];
//create lists of all the similar groups (if 1 and 2 are similar, and 2 and 3 are similar, the group is 1, 2, 3)
for (let i = 0; i < similarSponsors.length; i++) {
if (dealtWithSimilarSponsors.includes(i)) {
//dealt with already
continue;
}
//this is the group of indexes that are similar
let group = similarSponsors[i];
for (let j = 0; j < similarSponsors.length; j++) {
if (group.includes(similarSponsors[j][0]) || group.includes(similarSponsors[j][1])) {
//this is a similar group
group.push(similarSponsors[j][0]);
group.push(similarSponsors[j][1]);
dealtWithSimilarSponsors.push(j);
}
}
similarSponsorsGroups.push(group);
}
//remove duplicate indexes in group arrays
for (let i = 0; i < similarSponsorsGroups.length; i++) {
uniqueArray = similarSponsorsGroups[i].filter(function(item, pos, self) {
return self.indexOf(item) == pos;
});
similarSponsorsGroups[i] = uniqueArray;
}
The system creates groups of similar sponsors that are all similar to each other. For example, the first similar sponsor finding function might find groups such as [[1, 2], [5, 2], [7, 3]], these get grouped up into groups based on duplicates into an array like this [[1, 2, 5, 2], [7, 3]]. The duplicates are then removed, making the groups of similar sponsors [[1, 2, 5], [7, 3]].
Out of each of these groups, only one sponsor is chosen to be sent out to the user. This function finds a weighted random choice for each group in the array.
//gets the getWeightedRandomChoice for each group in an array of groups
function getWeightedRandomChoiceForArray(choiceGroups, weights) {
let finalChoices = [];
//the indexes either chosen to be added to final indexes or chosen not to be added
let choicesDealtWith = [];
//for each choice group, what are the sums of the weights
let weightSums = [];
for (let i = 0; i < choiceGroups.length; i++) {
//find weight sums for this group
weightSums.push(0);
for (let j = 0; j < choiceGroups[i].length; j++) {
//only if it is a positive vote, otherwise it is probably just a sponsor time with slightly wrong time
if (weights[choiceGroups[i][j]] > 0) {
weightSums[weightSums.length - 1] += weights[choiceGroups[i][j]];
}
}
//create a random choice for this group
let randomChoice = getWeightedRandomChoice(choiceGroups[i], weights, 1)
finalChoices.push(randomChoice.finalChoices);
for (let j = 0; j < randomChoice.choicesDealtWith.length; j++) {
choicesDealtWith.push(randomChoice.choicesDealtWith[j])
}
}
return {
finalChoices: finalChoices,
choicesDealtWith: choicesDealtWith,
weightSums: weightSums
};
}
The randomly weighted choice is calculated in this function:
//gets a weighted random choice from the indexes array based on the weights.
//amountOfChoices speicifies the amount of choices to return, 1 or more.
//choices are unique
function getWeightedRandomChoice(choices, weights, amountOfChoices) {
if (amountOfChoices > choices.length) {
//not possible, since all choices must be unique
return null;
}
let finalChoices = [];
let choicesDealtWith = [];
let sqrtWeightsList = [];
//the total of all the weights run through the cutom sqrt function
let totalSqrtWeights = 0;
for (let j = 0; j < choices.length; j++) {
//multiplying by 10 makes around 13 votes the point where it the votes start not mattering as much (10 + 3)
//The 3 makes -2 the minimum votes before being ignored completely
//https://www.desmos.com/calculator/ljftxolg9j
//this can be changed if this system increases in popularity.
let sqrtVote = Math.sqrt((weights[choices[j]] + 3) * 10);
sqrtWeightsList.push(sqrtVote)
totalSqrtWeights += sqrtVote;
//this index has now been deat with
choicesDealtWith.push(choices[j]);
}
//iterate and find amountOfChoices choices
let randomNumber = Math.random();
//this array will keep adding to this variable each time one sqrt vote has been dealt with
//this is the sum of all the sqrtVotes under this index
let currentVoteNumber = 0;
for (let j = 0; j < sqrtWeightsList.length; j++) {
if (randomNumber > currentVoteNumber / totalSqrtWeights && randomNumber < (currentVoteNumber + sqrtWeightsList[j]) / totalSqrtWeights) {
//this one was randomly generated
finalChoices.push(choices[j]);
//remove that from original array, for next recursion pass if it happens
choices.splice(j, 1);
break;
}
//add on to the count
currentVoteNumber += sqrtWeightsList[j];
}
//add on the other choices as well using recursion
if (amountOfChoices > 1) {
let otherChoices = getWeightedRandomChoice(choices, weights, amountOfChoices - 1).finalChoices;
//add all these choices to the finalChoices array being returned
for (let i = 0; i < otherChoices.length; i++) {
finalChoices.push(otherChoices[i]);
}
}
return {
finalChoices: finalChoices,
choicesDealtWith: choicesDealtWith
};
}
This makes it so that the user gets only one of the sponsors, but some users might get some lower rated sponsors, to give them a chance of getting more ratings.
But won't people be frustrated getting terrible submissions?
See this formula again.
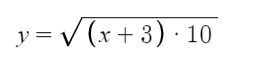
Because of this formula, if a sponsor has a number of votes (x) that is -3, their chance will be zero. Below that, it is an undefined result, so before feeding the numbers to this function, those are weeded out.
-2 was chosen since it allows 2 people to accidentally click downvote before the submission gets ignored entirely. I feel it is a good balance to prevent troll votes from making all times disappear. Of course, this could be modified a bit in the future.
Preventing user from getting bombarded with skips
To prevent there being too many non similar sponsor times, after all these calculations have taken place, if there are more than 4 sponsor times to send out, it gets the best 4 using the weighted random function.
finalSponsorTimeIndexes = getWeightedRandomChoice(finalSponsorTimeIndexes, votes, 4).finalChoices;
To be more fair to sponsor times with multiple similar sponsor times, the sum of all the positive votes on similar sponsor times is used as the weight for the chosen sponsor time.
Notice
The server is temporarily down and should be back up in a few days. Better uptime will happen once this project has reached beta, which should be in a week or two.
Pull Requests
https://github.com/ajayyy/SponsorBlock/pull/2
https://github.com/ajayyy/SponsorBlockServer/pull/2
https://github.com/ajayyy/SponsorBlockServer/pull/3
Thank you for your contribution. Interesting project!
for (var j = i + 1instead ofj = 0.[...new Set(Array)]see thisYour contribution has been evaluated according to Utopian policies and guidelines, as well as a predefined set of questions pertaining to the category.
To view those questions and the relevant answers related to your post, click here.
Need help? Chat with us on Discord.
[utopian-moderator]
Thanks for your suggestions, I'll look into adding those.
No, it's not on the chrome store yet, but it should be by the end of this week. (hopefully)
Thank you for your review, @justyy! Keep up the good work!
Hey, @ajayyy!
Thanks for contributing on Utopian.
We’re already looking forward to your next contribution!
Get higher incentives and support Utopian.io!
Simply set @utopian.pay as a 5% (or higher) payout beneficiary on your contribution post (via SteemPlus or Steeditor).
Want to chat? Join us on Discord https://discord.gg/h52nFrV.
Vote for Utopian Witness!
This post earned a total payout of 19.647$ and 14.772$ worth of author reward which was liquified using @likwid. To learn more.