Днями побачив цікаву задачу, а шлях до розв'язку відразу було не видно. А насправді розв'язок знайшовся швидко.
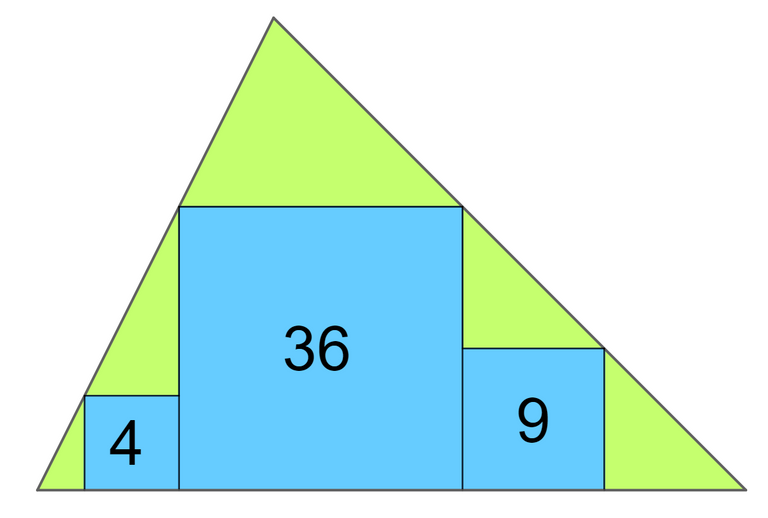
У трикутник вписано три квадрати площа яких 4, 36 та 9 см2. Знайти площу трикутника.
Малюнок до задачі я побудував у Geogebra.
- спочатку провів пряму.
- відклав відрізки заданої довжини: 2,6,3
- побудував на них квадрати.
- через вільні вершини квадратів провів прямі які й утворили трикутник.
Але тут мені закортіло буквально вписати три квадрати в трикутник
Довелося трохи подумати над залежностями - тобто що рухати(який параметр буде змінюватися) щоб GeoGebra будувала три квадрати.... знайшов!

Будую трикутник ABC та обираю точку на об'єкті - точку D на AC.
і...я зайшов у тупик.
Задача(побудови малюнка, а не знаходження площі) звелася до вписування квадрата у трикутник.
Вписувати коло нас учили в 7 класі... а от вписати квадрат....??
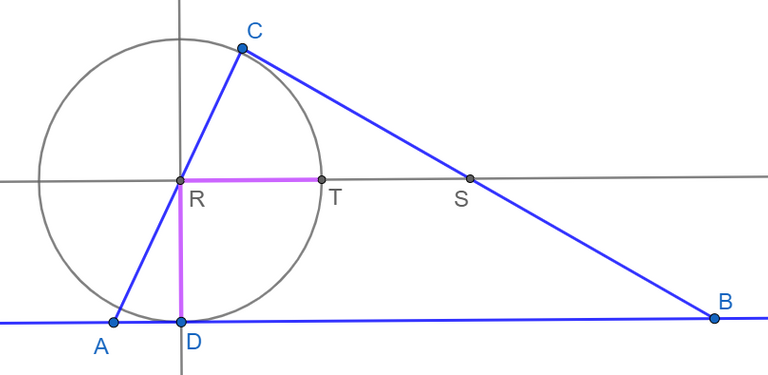
Я хотів щоб від положення точки D залежало положення трьох квадратів,
тоді як воно однозначно визначається самим трикутником.
І я зайшов у тупик, як же побудувати цей однозначно визначений квадрат?
З точки D перпендикуляр до перетину зі стороною, потім ще перпендикуляр до перетину з іншою - але ж відстань буде інша...
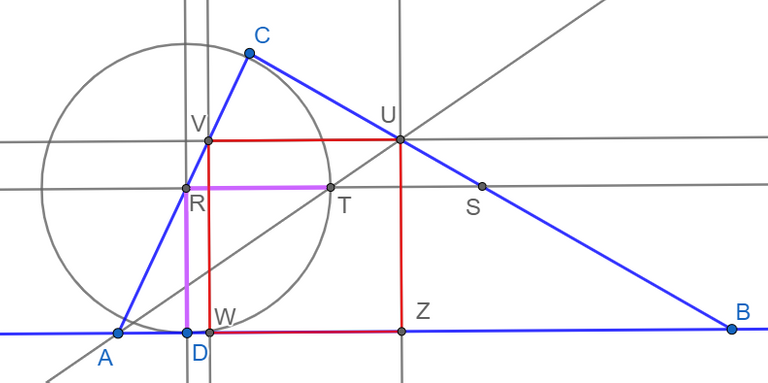
Я довго думав як же рухаючи точку D зробити так, відрізки RT та RD залишалися рівними, і щоб точки T і S співпали...
..треба провести пряму AT вона і перетне сторону BC у шуканій точці U. Опустимо з точки U перпендикуляр UZ на сторону AB. Це і буде сторона квадрата. Провівши ще паралельні(перпендикулярні) прямі знайдемо шуканий квадрат.
Пряма АУ перетне сторону VW в точці H і HW буде стороною лівого квадрата.
А пряма VB перетне сторону UZ в точці G і GZ стороною правого квадрата.
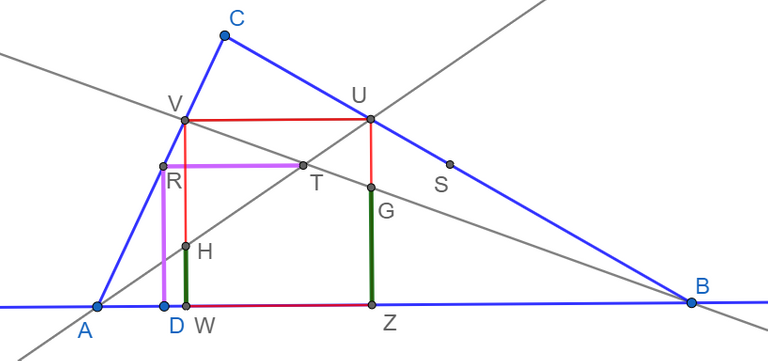
Будуємо на вказаних відрізках квадрати.

Готово!

Повернемося до задачі, умова:
У трикутник вписано три квадрати площа яких 4, 36 та 9 см2. Знайти площу трикутника.
Розв'язування покажу пізніше.