This is the second part of the introduction to machine learning serie.
In the previous blog I introduced the basic ideas of neural networks. In this post I’ll be talking about the technique behind deep learning the thing that in recent years enabled all the amazing technologies - from google image search, DeepDream to self-driving cars.

So, how does it work?
In the last post I described the math behind the learning and using of the shallow networks. The question is how can one build the deep network starting from the basic paradigm of neural networks - the weighted graph with neurons as nodes, the learning of the networks via backpropagation, and the universal approximation capability of neural network.
In theory you could just repeat the layers of normal neural network many times and build a deep neural network. In practice you stumble upon two problems. If you repeat it with the basic network you get a huge network that first of all won't fit into any memory, secondly would be practically untrainable because of the vast amount of parameters and thirdly would needlessly repeat and learn the same pattern (pattern = face, cat, anything) for all different displacements of it in the input. The answer to this problem are convolutional neural networks that I’ll now explain with all the math behind it.
Deep learning
In the past years artificial neural networks became the leading algorithms for many computer vision tasks such as image classification, segmentation and other. This recent growth of interest in neural networks was triggered by the successes of deep learning which enabled leveraging the vast amounts of available training data and increasing computational power.
Unlike the typical shallow neural networks (up to 3 layers) the deep architecture can efficiently train larger number of parameters and therefore approximate high complexity functions, which are necessary for solving difficult problems such as computer vision or natural language processing. The deep layered model can learn better representations of the input data, and subsequently be trained more efficiently.
The fundamental concept of deep learning algorithms is the idea that the input data have underlying representation, which is composed of various levels of abstraction from simple to more abstract concepts. This notion is used by the deep learning algorithms to extract the important features from the data through cascading many nonlinear processing units. The layers are forming a hierarchy, where the higher level features are build upon the lower level features. By varying the number of layers, different level of abstraction can be achieved.
Convolutional neural networks
The convolutional neural networks (CNNs) are often used to enable training of deep learning algorithms. The CNN model is based on the traditional neural network model, however unlike the standard model of neural network, which is hard to train as deep architecture due to high amount of parameters. However, CNN models can be built very deep and still be efficiently trained through backpropagation. The efficiency of the CNN model comes from accounting for the local correlation present in images, which enables it to have much less parameters to train than a neural network model would have and still be able to find complex patterns in the presented data.
The architecture of CNN was inspired by the study of Hubel and Wiesel from early 1960's. They described the overlapping receptive fields in animals' eyes and the existence of simple and complex cells within the visual cortex. Upon those observations they described the existence of a hierarchical arrangement, that would make the cells in the visual cortex process increasingly more complex patterns from spots and edges up to entire objects. The first commonly known work that followed upon the ideas of Hubel and Wiesel was LeCun's work from 1998 (nowadays known as LeNet. LeCun showed the exceptional characteristics of CNNs and the use of spatial correlation in pictures. The work showed the superior performance of machine learning based approach to feature extraction in comparison to hand-crafted selection of features. The model combined convolutional feature extractor with classifier atop, and it was trained jointly with backpropagation.
The basic ideas exploited by the CNN architecture are local connectivity and weight sharing. Local connectivity exploits the spatially local correlation of pixels in natural images by always connecting neurons only to a small section of input from the preceding layer. By stacking several of those layers, the neurons in the higher layers become more global by reacting on larger section of the input image. They respond to more complex patterns than neurons in the lower layers as can be seen in the image bellow.
Second main contribution of the CNN model is the sharing of weights. It reduces the number of parameters by applying each filter which is also called kernel across the whole input. By applying one kernel on the input we receive a feature map which together with other feature maps from other kernels forms the input to the next layer.

Courtesy of http://deeplearning.net/tutorial/lenet.html
Since the year 2012, the CNN-based models are the most successful models at many vision task. The breakthrough was brought by the work of Krizhevsky et al. (Imagenet classification) who decreased the error rate at the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) by about 10%. This major improvement in accuracy of the classification was achieved mainly thanks to two changes: the introduction of the non-saturating activation function ReLU and the usage of dropout (regularization method) to prevent overfitting, which enabled them to train a model consisting of 650.000 units with 60 million parameters.
A typical convolutional neural network consists of convolutional layers that create feature maps, alternated with the max-pooling layer for resizing of the processed data and sometimes also regularization techniques such as dropout, batch regularization etc.. At the top of the convolutional layers there can be the typical (fully-connected) neural network (for object classification) or a recurrent network (for text classification).
A typical convolutional network
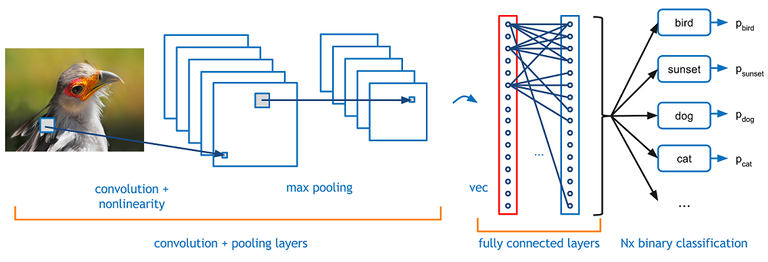
Courtesy of DeepLearningBlog
Convolutional layer
Convolution is a mathematical operation of two functions, it is denoted by f * g. The basic equation for convolution of functions f and g is

In the case of convolutional neural networks the applied convolution is discrete

Specifically for convolutional layers the outputs of all units y_ij, where i and j are 2D coordinates of the input, in a layer l and kernel k are calculated by first calculating the inner activation of neuron x_ij^l:

where the filter is of size mxm, y^l-1 is the output from preceding layer, w_ab are weights in the applied filter. The non-linearity f - usually a ReLU activation function (see [previous post]) - is then applied to the activation from convolution.

The ReLU activation function was the answer to the problem of vanishing or exploding gradient which is another issue that arises with building deep architectures. Unlike the sigmoid or tanh activation function it doesn’t saturate so easily (saturation = state of the neuron when it returns always gradients at 0 which disables learning of weights below the neuron).
The weights applied in convolution are grouped in the kernels (see figure). The same kernel is applied across the whole input, this process is also called weight sharing. The output of the application of one or more kernels is a convolutional layer. During training the weights of the convolution are updated by the selected optimization method, which results into the specialization of the kernel on a specific pattern which can occur anywhere in the picture, it is translation-invariant. The usual size of kernels ranges from 3x3 up to 7x7 input units.

Courtesy of http://deeplearning.net/tutorial/lenet.html
The size of the output from the convolutional layer is determined by the number of kernels, the size of kernels, stride, and padding. Stride defines the size of the overlap of the receptive fields of neurons and thus the shift of the kernel, and padding is usually used to prevent losing the information from the boundaries of the inputs and to prevent premature downsizing of the feature maps. The value of padding is typically 0.
Important notion in the convolutional neural networks is the receptive field of a neuron. It corresponds to a local region in the input data that influence the specific neuron. Between two successive layers the receptive field of a neuron is equivalent to the region in the previous layer in size of the applied kernel. By stacking more CNN layers on top of each other the neurons in higher layers are sensitive to increasingly larger receptive field in the original input image.
Max-pooling layer
Another part of the convolutional neural network architecture is the max-pooling layer. It is a non-trainable layer that carries out a simple operation that results in the reduction of size of the model, it is usually applied in-between two successive convolutional layers. The idea of max-pooling comes from the fact, that the information in images is usually not restricted to a single pixel, but rather spread in groups of pixels, that all carry similar information. Therefore the size of the data can be reduced by leaving out some of those pixels without the loss of the important information.
The max-pooling operation takes the maximal value from a window of size kxk. The operation is applied across the whole input with a given stride.
Regularization methods
One of the problems of the basic deep neural networks was the overfitting of the models to the training data. The way to solve this problem is by using some regularization technique such as dropout, unit pruning, weight decay, or batch normalization.
The dropout is the most popular regularization method. When using dropout some randomly selected units are temporarily removed from the model in each training iteration. This way the model avoids learning rare dependencies in the training data that could lead to over-fitting.
Another problem related to the training of deep networks is that the distribution of inputs in each layer is shifting based on the change of the previous layer. This problem can be overcome by batch normalization. With this technique layer inputs are normalized over each training batch which is a subset of the training dataset which losses are summed together and backpropagated in one backward pass. The normalized value is then transformed by weights, which are trained along with other parameters of the model.
And that’s it!
The convolutional neural networks overcome the three problems that I introduced at the beginning of the post and since the 2012 breakthrough they’re unbeatable for the classification tasks (what’s on the picture). In recent years they became the leading algorithms in all other areas - object detection (where is it on the picture), object segmentation (prediction for each pixel what object it belongs to), text reading systems and many other tasks.
All of the recent successful models (from VGGnet to Google Inception modules) are implemented in all the popular frameworks for machine learning - mainly neural networks such as Tensorflow, Keras, Torch, Caffe, Theano… So it is very easy to start off just by using those models, taking the pretrained model and see for oneself how it classifies, you can of course also train a model for yourself, however it requires a good gpu (with big enough memory).
And this is what you can get (well if you're as good as Microsoft research - or just use their model)

I hope you enjoyed the second part of the introduction and next time I’ll explain the recurrent neural networks.
mor. hello
Post. immediate Ctrs+S without questions:)
Deutsch rap? Nice.. :)
...
...
I got some feedback on the steemSTEM that I should divide the (next) posts into smaller chunks. If you also think so, please tell me.
People on the internet are busy... being on the internet. So maybe it would make it easier for them. I wrote a very long post about choosing a name in Japanese and Chinese, and not many people had the patience it seems.
Really interesting. Thanks for sharing!
Great thanks ...