The Equations
First, let's get on right away with the equations.

If your reaction is the same as mine when I was introduced to these equations (confusion), then you are in the right place! :-)
Note about vector representation in this post: Unfortunately due to the poor support of arrow headed characters throughout browsers, the text will refer to vector fields without using the arrow over the field character. For example, E refers to the Electric vector field.
Let's break down the equations into their individual symbols and operators. A clear explanation of each element is given further in this post.
- ∇: This is the DelGradient operator. It is represented by the Nabla symbol, which is an upside down version of the Δ (delta) greek letter.
- ρ: The electric charge density
- ε0: The permittivity of free space (vacuum).
- E: This is the electric field.
- B: This is the magnetic field.
- J: This is the current density.
- ∂: The differential operator.
- μ0: The permeability of free space (vaccum).
- c: The speed of light in vaccum.
- .: The dot product
- xX: The *cross product
- t: represents time.
OK, that's a mouthful of symbols to digest.
For now, let's ignore the equations and get a better understanding of all the above concepts.
What is a 'Field'?
In physics a field is a quantity that has a value in each point of space and time.
Fields can be of different natures:
scalar field. Each point in the field has a single/dimensionless value: a numerical value and unit. For example, one can define the temperature field where each point in space/time has a precise value in Celcius or other temperature units.
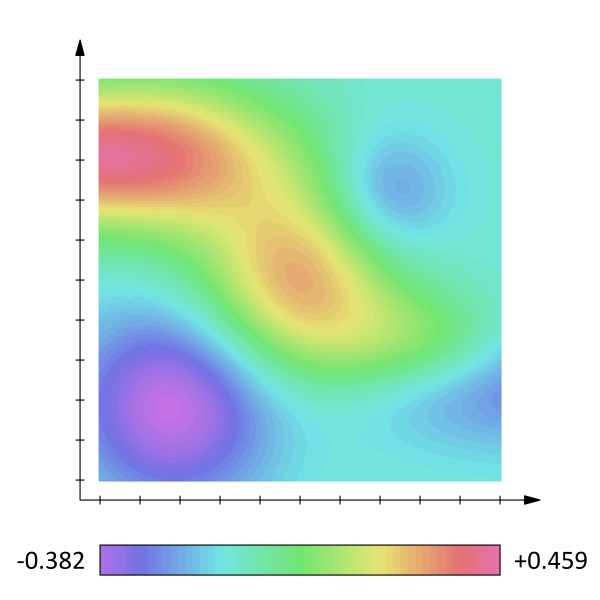
Example scalar field. Each point value is represented by a color.
Image Credit: Lucas V. Barbosavector field: Each point in this field has a value that can be represented by a vector. That is, a direction and an amplitude. For example, this type of fields could be use to represent wind direction and strength in meteorology.

Example vector field. Each point value is represented by a vector.
Image Credit: Jim.belk
There are other types of fields such as spinor fields and tensor fields, however these are beyond the scope of this article.
In the Maxwell Equations, the electric field and magnetic field are vector fields.
The electric field E and the magnetic field B are both fundamental fields of nature which are influenced by the presence of electric charges.
An electric charge causes an excitation of the electric field which causes the field to have a non-zero value within the surrounding of the charge.
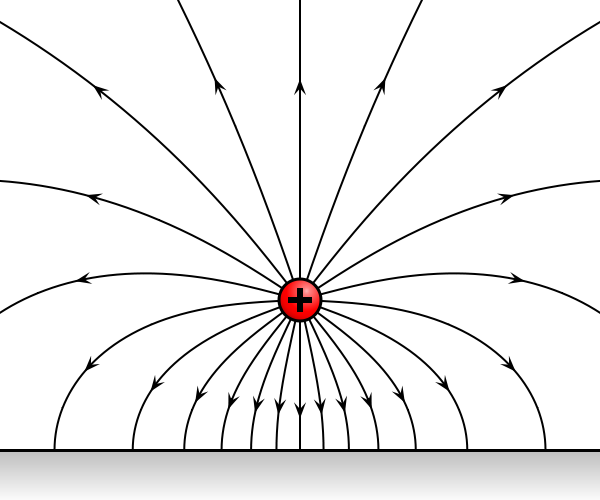
Electric field around a charged particle
Credit: Geek3
As a result, another electric charge within this region of space is subject to a repelling or attractive force depending on whether or not both charges are of the same or opposite sign.

Electric field between two oppositely electric charged particles.
Credit: Geek3
The magnetic field, B, is also a vector field. Like the electric field, the magnetic field can be excited by the presence of electric charges in two ways:
- Moving electric charges causes excitation of the magnetic field. This phenomenon is used, for example, in electromagnets where an electric current is produced to generate a strong magnetic field (more later about this).
- Excitation of the magnetic field can also be induced by the intrisic magnetic moment of some elementary particles.
In a similar way to the electric field, the magnetic field causes repelling or attractive forces on electrically charged particles.
For example, a charged particle moving within a non-zero magnetic field is subject to the Lorentz Force
Magnetic fields are traditionally demonstrated in school using iron filings spread over a hard surface covering a permanent or electro magnet:
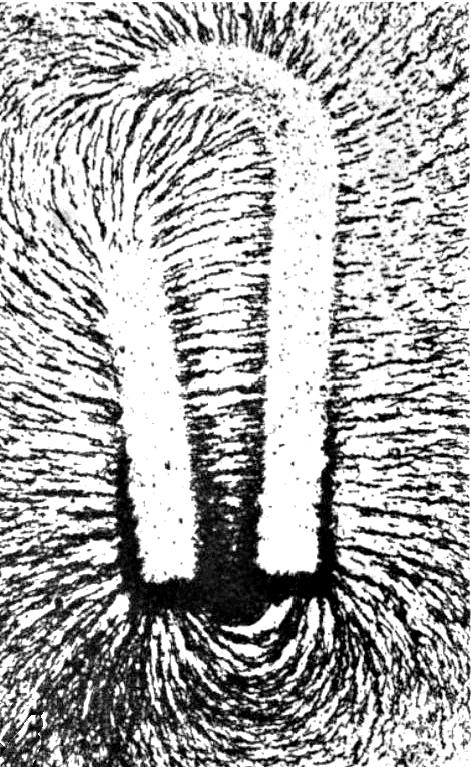
Iron filings spread over permanent horseshoe magnet
Credit: Frank Eugene Austen
What is the 'Differential Operator'?
The differential operator, ∂, is used in differential calculus and represents the effect of an infinitesimal (infinitely small but non-zero) change of a variable in a function on the output value of that function.
For example, the term:
∂B/∂t represents the change in the magnetic field over an infinitesimally small amount of time.
So where ∂BLA/∂t is used in an equation, it involves the variation of "BLA" over time.
So differential calculus deals with dynamic systems.
In the Maxwell Equations, the differential operator explicitely appears in the form ∂/∂t which indicates that the equations describe a change over time of other depending quantities. This is described further in this post.
Charge Density
The charge density, ρ, simply describes the amount of electric charges per unit of volume (Coulombs per cubic meter)
Permittivity and Permeability
The permittivity, ε, describes the amount of charges required to excite the electric field E to a certain value.
This amount of charges depend on the medium within which the electric charges operate.
Some mediums are very prone to excitation of the electric field, while others "resist" the excitation of the electric field.
ε is thus a constant which depend on the medium.
ε0 represents the permittivity of free space (vacuum).
The permeability, μ is to the magnetic field B what the permittivity is to the electric field E.
In other words, the permeability represents the resistance of a particular medium to the excitation of the magnetic field.
μ0 is the permeability of free space (vacuum).
Now, are the permittivity and the permeability of a particular medium independent from each other?
The answer is no!
Interestingly, the permittivity and the permeability are related to each other through the speed of light. In free space, this relationship is as follows:
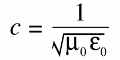
This equation is the first clue that the electric field, the magnetic field and the speed of light are intimately related. Here, "light" should be considered to be a wave within the electric and magnetic (electromagnetic) field.
The above equation takes the following form in other mediums:
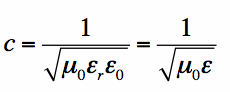
Where εrε0 = ε, the permittivity of the medium.
So the higher the permittivity of the medium, and the slower is the speed of an electromagnetic wave within this medium.
What is the 'Del' Operator?
The 'Del' operator, represented by the Greek letter nabla ∇, is a generalization of the differential operator described above.
Where the differential operator represents an infinitesimal change of a single scalar (dimensionless) variable, the ∇ operator represents the effect of an infinitesimal change of given multi-variable function for all of its components.
For example, imagine the value of the electric field, E, at a specific point in space and time. This value can be represented on a diagram as a vector.
The term ∇E describe how that vector value would change when moving to an infinitesimally close point in each one of the three dimensions of space.
That is, the electric field value (a vector) changes by some small value which can be described by a change in direction and amplitude.
In summary, the ∇ operator describes how a system (described by a multivariable function) changes within its immediate surroundings.
The ∇ operator can be combined with two other vector operators, the 'dot' operator (.) and the cross operator (x) in what is referred to as divergence and curl.
What is 'Divergence'?
The 'dot' product, symbolized by a '.' symbol is an operator between two vectors that indicates, among other things, how aligned these two vectors are.
When combined with the ∇ operator, the resulting operation ∇. is called divergence and represents for every point in space the net contribution of all field values within the immediate surroundings of that point.
To understand divergence, let's visually represent the presence of a positive and negative charge (a dipole) in an electric field.
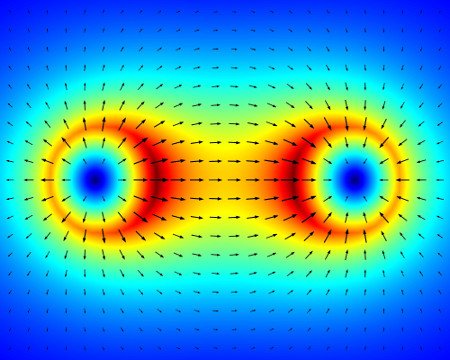
Electric field around a dipole. Positive charge on the left and negative charge on the right.
Credit: James R. Nagel
Imagine now that the electric field vectors on the above diagram represent the flow of fluid around the system.
As one can see, this imaginary flow field would seem to emanate from the positive charge on the left, while it seems to converge and be absorbed towards the negative charge on the right.
The area around the positive charge (left) is commonly referred to as a source, while the area around the negative charge (right) is referred to as a sink.
Within a certain region of space, the divergence refers to the net amount of field "flowing" out against the amount of field "flowing" in of that area. If this net amount is positive (more "flowing out" than "flowing in"), then the divergence is positive. Otherwise the divergence is negative.
An area in space where the divergence is 0 corresponds to a region where the imaginary flow "flowing in" exactly matches the amount of imaginary flow "flowing out".
In fluid mechanics, the field representing the motion of a fluid whose divergence can only be zero at all points characterizes the incompressibility of that fluid.
What is 'Curl'?
The 'cross' operator applied to two vectors indicate, among other things, how orthogonal these vectors are to each other.
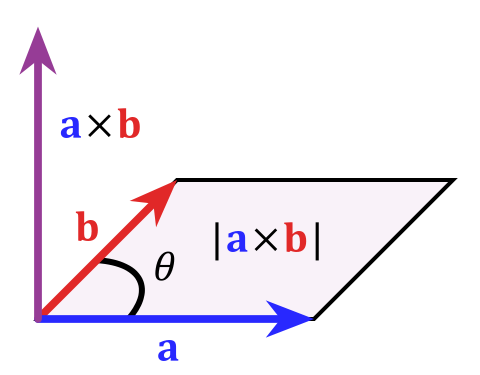
Vector cross product
Credit: Acdx
As one can see in the diagram above the result of the cross product is maximized when the operand vectors a and b are orthogonal, while it is 0 when θ is zero.
When combined with the ∇ operator, the resulting ∇x operator is referred as the curl operator.
The curl of a vector field at a particular point in space represents the tendency of the field to swirl around that point, that is the tendency to follow a non-linear direction.
For example, in the previous example of two opposite charges:

one can see that around the imaginary line connecting the two charges, the field follows a linear path, yielding a curl value around that region close to 0.
On the other hand, the field follows a very non-linear path in the corner regions of the image. These regions correspond to a large curl value and indicates that the field swirls significantly clockwise (negative curl) or anti-clockwise (positive curl).
Armed with our new understanding of the mathematical elements previously described, we can now start examining each one of the Maxwell Equations.
It should be noted that Maxwell did not discover these equations out of nothingness.
Various laws of electricity and magnetism had already been discovered by other scientists such as Michael Faraday, Johann Carl Friedrich Gauss and Charles-Augustin de Coulomb.
By the mid-19th century it was clear that the laws of electricity and magnetism were tightly coupled, but the task remained to unify those laws into one set of generalized laws of electromagnetism.
The First Law explained
Let's review the equation for the first law:
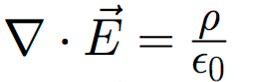
It reads as follows:
The divergence of the electric field in a certain region of space is proportional to the charge density in that region.
Recall that ε0 is the permittivity of free space and is a constant, so ignoring for a moment this term does not affect the overall meaning of the equation.
This is a reformulation of the Gauss's law.
It describes how a volume of space enclosing a certain amount of electric charges results in a non-zero electric field proportional to this electric charges.
It also describes how electric lines within the field diverge away from a positive electric charge (source) and converge towards a negative charge (sink).
A closed surface enclosing a net negative charge result in a net electric field. That is, a negative charge located within the surface of that volume is subject to a repulsive force with strength proportional to the electric field value at that location.
Similarly, a positive charge located at that same location is subject to an equivalent attractive force.
The exact intensity and direction of the force requires solving the equation and is not within the scope of this post.
Another interesting conclusion of the above is that if the closed surface in question does not enclose any electric charge, then the divergence of the electric field affecting the volume must be zero.
That is, the inbound electric lines and outbound electric lines must cancel out exactly.
In other words, the electric field is conserved within a region of space not enclosing any electric charge.

Conservation of electric field within a closed surface not enclosing any electric charge
Credit: Homer Holmes - Steps to applying Gauss' Law
The Second Law explained
The second law is as follows:
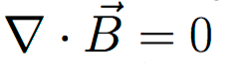
It is very similar to the first law but applies to the magnetic field and specifies that:
The divergence of the magnetic field is null everywhere.
It is also known as Gauss's law for magnetism.
In other words, The magnetic field is conserved everywhere.
That is, a magnetic source cannot exist on its own and must be accompanied by an equivalent magnetic sink.
This magnetic source and sink are commonly referred to as magnetic poles.
So this equation states that a magnetic "north" pole cannot exist without a magnetic "south" pole, and the magnetic lines of the magnetic field B flow between these two poles.
Note the difference with the first equation which states that an electric charge (i.e. an electric field sink/source) can exists on its own.
While the electric field can have infinite, unterminated, electric lines, a magnetic field must originate from a magnetic pole and terminate at another opposite magnetic pole.
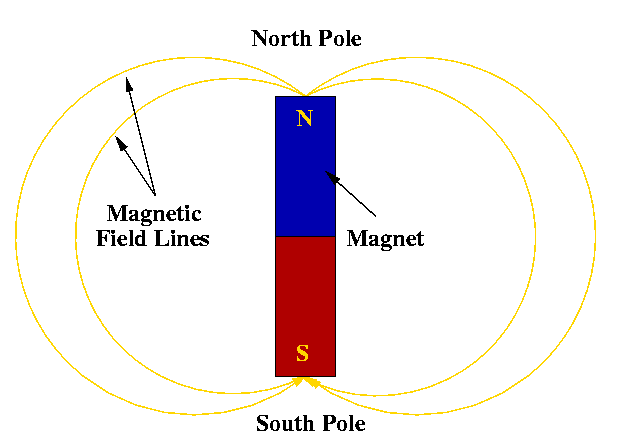
Magnetic dipole and simplified magnetic field
Credit: Magnetism on Emporioworld.com
The Third Law explained
This equation reads:
A variation of the magnetic field over time induces an electric field in a plane orthogonal to this magnetic field.
This is reformulation of Faraday's law of induction.
It explains how a magnet moving along the axis of a closed conductive wire would cause an electric current within the wire.
Note that the reverse is also true.
So, an electric charge moving in a certain direction induces a magnetic field in a direction orthogonal to the charge.
This principle is used by most modern electric motors.
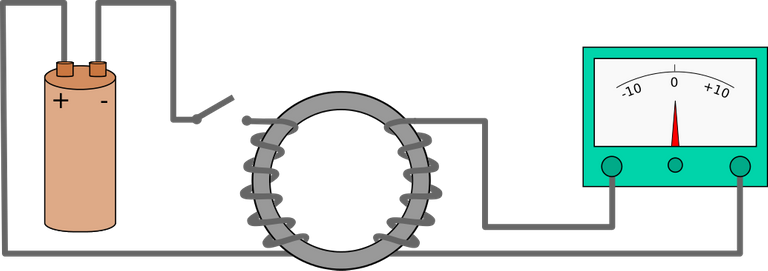
Farady iron ring apparatus
Credit: Eviatar Bach
The above illustration shows how Faraday iron ring apparatus can be used to demonstrate Maxwell's third law.
A variable magnetic field in the left conductive coil induces an electric field and, as a result, an electric current in the coil circuit on the right hand side.
The Fourth Law explained
Finally let's examine the fourth law:
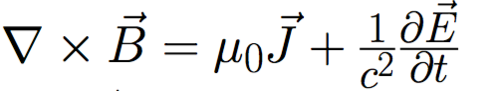
This is a generalization of Ampere's circuital law which states that an electric current flowing through a wire generates a magnetic field that is orthogonal to the wire and "curls" around it.
This is the ∇xB = μ0J part of the equation, where J is a steady current flowing through the wire.
Now, recall from the third equation (Faraday's law) that a variable magnetic field generates an electric field.
Maxwell's insight was to think that the reverse might be true.
And so, Maxwell added a second term representing an electric field changing over time and also providing a contribution to the magnetic field.
In other words, Maxwell generalized Ampere's law by stating that a magnetic field can be generated as a result of two phenomena:
- contribution from an electric current flowing through a conductive material (Ampere's law), and
- contribution resulting from the variation of the electric field. Note that this contribution does not require any medium!
The fourth law then reads something like:
The magnetic field surrounding a wire is a function of the steady electric current passing through the wire plus a contribution induced by the variable electric flux around the wire.
Notice that there is an important snowball effect between the third and fourth law:
A variable magnetic field induces a variable electric field (third law), but in return the variable electric field gives rise to a variable magnetic field (fourth law)!
The fourth law is now critical because it indicates that even in the absence of an electric current, a variable electric field induces an orthogonal variable magnetic field, without the need for any medium. And by applying the third law, this variable magnetic field also induces a variable electric field!
What Maxwell described throught the 3rd and 4th equations is a pair of self-sustaining oscillations in the electric field and the magnetic field in a vacuum: an electromagnetic wave propagating through the vacuum!
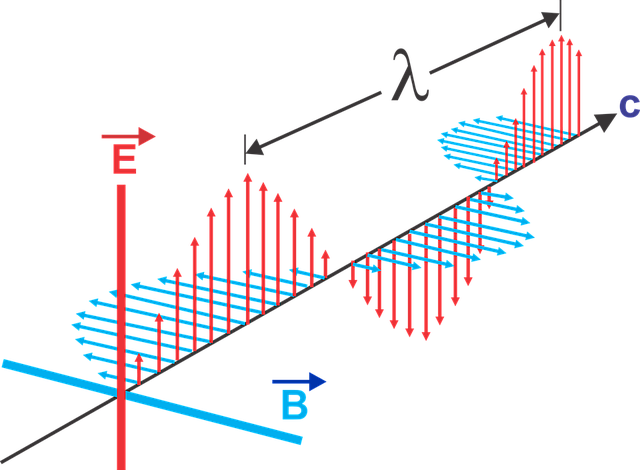
Orthogonal electric and magnetic waves propagating through the vacuum: an electromagnetic wave!
Credit: https://pixabay.com/en/electromagnetic-waves-wave-length-1526374
Through deep reasoning and a leap of imagination, Maxwell had predicted the existence of electromagnetic waves!
And what about the speed of this electromagnetic wave? Well, the speed of light, of course!
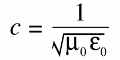
This discovery would pave the way for the invention of radio transmission technologies and bridge the world of classical electromagnetism of the 19th century to the golden era of modern physics of the 20th century.
Let's review what we've learned!
The story of how Maxwell came to discover and prove his pivotal equations is a strong reminder for the famous quote:
If I have seen further it is by standing on the shoulders of Giants.
-- Isaac Newton
James Clerk Maxwell took all the knowledge of the time regarding the laws of electricity and magnetism, generalized and unified them into a set of four fundamental equations establishing the intimate relationship between electric and magnetic field.
He formalized how charge density results in the shape of the electric field and how the lines of a magnetic field can only extend between two opposite magnetic poles.
He described through differential calculus how variations in the electric field induces a variable magnetic field and how the reverse holds true.
By doing so, he predicted the propagation of in-phase, orthogonal electric and magnetic waves, commonly referred to as an electromagnetic wave and how this wave would travel through space at the speed of light.
His formalization of the laws of electromagnetism paved the way for the development of radio transmission technologies and the connected world that we live in today.
Please check the last two references below for very interesting videos on YouTube about this subject.
References
- Fields (physics) on Wikipedia
- Electric Field on Wikipedia
- Magnetic Field on Wikipedia
- Lorentz Force on Wikipedia
- Del Operator on Wikipedia
- Differential Calculus on Wikipedia
- Homer Holmes - Steps to applying Gauss' Law
- Gauss's law for magnetism.
- Ampere's circuital law on Wikipedia
- 3Blue1Brown Youtube channel: Divergence and curl: The language of Maxwell's equations, fluid flow, and more
- Maxwell Equations - The Mechanical Universe on YouTube
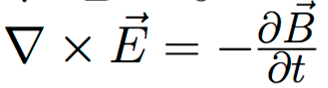
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
This is BRILLIANT! This is what the world needs (*should...)
One Perfect Explanation, from A to Z. Nothing else to add, nothing to remove. J.Peterson was thinking out loud something like: "why do we need thousands of lectures, that will be used all across the world, all of them telling the 90% same thing in the same way, about the same topic. What we need is One Perfect Lecture". There is no value in producing countless copies of the same thing because the mutual information is very high.
What you demonstrated here could be the core example what should be done: more exhaustive than Quora, more user-friendly than any book, way more advanced than Wiki. If only you could add some option to edit/improve the answer...
I used the term "mutual information", thus, let it be the next Q
Good luck!
Thank you so much for such a nice comment.
I remember being frustrated in college by my lack of understanding of these equations and I'm happy that with the help of modern day Internet I was able to somewhat make things clearer in my head.
Editing the answer is possible, but the author of the answer post only (Steem enforces this).
However StemQ tries to promote other users to add elements of answer that haven't been provided yet.
If using the StemQ UI, simply click the "Answer" button and add your own answer.
If using another Steem App, simply make sure to create a post with the same title as the question, but substitute the "Q:" with "A:".
Also, make sure to use the "stemq" tag.
I create a feature-requests channel on our Discord server.
All suggestions are welcome.
Thanks again!
Ah Maxwell :) The math genius.
One of the most important equation in science.
He described the practical work than Faraday did with such an elegance.
This post is with super high quality. Excelent job. I wasn't even aware that there are such a things on Steemit.
Thank you so much! :-)
I am quite impressed by the amount of work you put into this post. Explaining difficult mathematical concepts to non-scientists is very difficult in my experience.
I saw some blanks in the text. Do you intend to fill them in with time?
Hi, thank you very much!
Woops, thank you for telling me about the blank sections.
I overwrote by accident an earlier draft of this article. :-(
I corrected the problem.
Thanks again!
Well I am glad I noticed it. I am actually kind of suprised no one noticed before with all the upvotes and stuff.
I actually updated the article later on because initially I had some vector characters which did not render properly in all browsers.
I messed up when I updated the post...
Hi @irelandscape!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
I upvoted your post.
Keep steeming for a better tomorrow.
@Acknowledgement - God Bless
Posted using https://Steeming.com condenser site.
Congratulations! Your post has been selected as a daily Steemit truffle! It is listed on rank 5 of all contributions awarded today. You can find the TOP DAILY TRUFFLE PICKS HERE.
I upvoted your contribution because to my mind your post is at least 12 SBD worth and should receive 169 votes. It's now up to the lovely Steemit community to make this come true.
I am
TrufflePig, an Artificial Intelligence Bot that helps minnows and content curators using Machine Learning. If you are curious how I select content, you can find an explanation here!Have a nice day and sincerely yours,

TrufflePigOverly neat, friend.
Maxwell's
equations to watch more videos play
subscribe to open vex education
Maxwell's first equation is Gauss law
this equation tells us that electric
field lines diverge outward from
positive charges and converge inward to
the negative charges
Maxwell's second equation tells us that
the magnetic field never diverges or
converge they always go around in closed
loops
therefore there doesn't exist a single
magnetic pole Maxwell's third equation
is Faraday's law this equation tells
that electric field lines curl around
changing magnetic fields and that
changing magnetic fields include
electric fields Maxwell's fourth
equation tells that magnetic field lines
curl around electric currents and that
magnetic field lines curl around
changing electric fields
Hi @irelandscape!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 3.100 which ranks you at #9296 across all Steem accounts.
Your rank has improved 301 places in the last three days (old rank 9597).
In our last Algorithmic Curation Round, consisting of 348 contributions, your post is ranked at #181.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
Simple. So gorgeous.
Hi, @irelandscape!
You just got a 5.78% upvote from SteemPlus!
To get higher upvotes, earn more SteemPlus Points (SPP). On your Steemit wallet, check your SPP balance and click on "How to earn SPP?" to find out all the ways to earn.
If you're not using SteemPlus yet, please check our last posts in here to see the many ways in which SteemPlus can improve your Steem experience on Steemit and Busy.