THE COMPRESSIBLE FLOW; OBTAINING MAXIMUM THRUST USING A CONVERGING-DIVERGING NOZZLE

INTRODUCTION

Generally, we have constrained our thought so far to streams for which thickness varieties and in this manner compressibility impacts are unimportant. In this section we lift this confinement and consider streams that include critical changes in density. Such streams are called compressible streams, and they are much of the time experienced in gadgets that include the stream of gases at high speeds. Compressible stream consolidates liquid progression and thermodynamics in that both are totally important to the improvement of the required hypothetical foundation. In this part, we build up the general relations related with compressible streams for a perfect gas with steady particular warms. We begin this part by presenting the ideas of stagnation state, speed of sound, and Mach number for compressible streams. The connections between the static and stagnation liquid properties are created for isentropic streams of perfect gases, and they are communicated as elements of particular warmth proportions and the Mach number. The impacts of territory changes for onedimensional isentropic subsonic and supersonic streams are talked about. These impacts are outlined by thinking about the isentropic move through merging and converging–diverging spouts. The idea of stun waves and the variety of stream properties crosswise over typical and slanted stun waves are talked about.


The investigation of gas elements is frequently connected with the flight of current fast air ship and climatic reentry of room investigation vehicles; notwithstanding, its starting points lie with less difficult machines. Toward the start of the nineteenth century, examination concerning the conduct of shot slugs prompted change in the exactness and capacities of weapons and artillery. As the century advanced, Scientists, for example, Gustaf de Laval propelled the field, while analysts, for example, Ernst Mach tried to comprehend the physical wonder required through experimentation.

STAGNATION PROPERTIES OF A COMPRESSIBLE FLOW

While breaking down control volumes, we think that its extremely advantageous to consolidate the internal vitality(energy) and the stream vitality of a liquid into a solitary term, enthalpy, characterized per unit mass as (h = u + P/D). At whatever point the kinetic and potential vatality of the liquid are irrelevant, as is regularly the case, the enthalpy speaks to the aggregate vitality of a liquid. For fast streams, for example, those experienced in jet nozzles, the potential vitality of the liquid is as yet irrelevant, yet the kinetic vitality isn't. In such cases, it is advantageous to join the enthalpy and the kineric vitality of the liquid into a solitary term called stagnation (or aggregate) enthalpy h0,defined per unit mass.


At the point when the potential vitality of the liquid is inconsequential, the stagnation enthalpy speaks to the aggregate vitality of a streaming liquid stream for every unit mass. In this way it disentangles the thermodynamic investigation of fast streams. All through this part the common enthalpy h is alluded to as the static enthalpy, at whatever point fundamental, to recognize it from the stagnation enthalpy. Notice that the stagnation enthalpy is a mix property of a liquid, much the same as the static enthalpy, and these two enthalpies wind up indistinguishable when the motor vitality of the liquid is immaterial. Consider the consistent stream of a liquid through a channel, for example, a spout, diffuser, or some other stream entry where the stream happens adiabatically and with no pole or electrical work. Assuming the liquid encounters next to zero change in its rise and its potential vitality, the vitality adjust connection (Ein to Eout).


Amid a stagnation procedure, the dynamic vitality of a liquid is changed over to enthalpy (internal vitality stream vitality), which brings about an expansion in the liquid temperature and weight. The properties of a liquid at the stagnation state are called stagnation properties (stagnation temperature,stagnation weight, stagnation thickness, and so on.). The stagnation state is known as the isentropic stagnation state when the stagnation procedure is reversible and in addition adiabatic (i.e., isentropic). The entropy of a liquid stays steady amid an isentropic stagnation process.

---

^{ALL STAGNATION POINT IN AN AEROPLANE: Creative CommonsAttribution-Share Alike 4.0 Internationallicense.}

---

SPEED OF SOUND AND MACH NUMBER

An essential parameter in the investigation of compressible stream is the speed of sound (or the sonic speed), which is the speed at which an imperceptibly little weight wave goes through a medium. The weight wave might be caused by a little unsettling influence, which makes a slight ascent in neighborhood weight. To get a connection for the speed of sound in a medium, consider a conduit that is loaded with a liquid very still, as appeared in Fig. below A cylinder fitted in the conduit is currently moved to one side with a steady incremental speed dV,creating a sonic wave. The wave front moves to the directly through the liquid at the speed of sound c and isolates the moving liquid neighboring the cylinder from the liquid still very still. The liquid to one side of the wave front encounters an incremental change in its thermodynamic properties, while the liquid on the privilege of the wave front keeps up its unique thermodynamic properties, as appeared in Fig. Below To disentangle the examination, consider a control volume that encases the wave front and moves with it, as appeared in Fig. below To an eyewitness going with the wave front, the liquid to the correct will give off an impression of being advancing toward the wave front with a speed of c and the liquid to one side to move far from the wave front with a speed of c Piston (dV h + dh) and (D + dD) Moving wave front (P + dP c + dPh) Stationary liquid . Obviously, the eyewitness will think the control volume that encases the wave front (and herself or himself) is stationary, and the spectator will witness an unfaltering stream process. The mass adjust for this single-stream, consistent stream process can be communicated as;

---

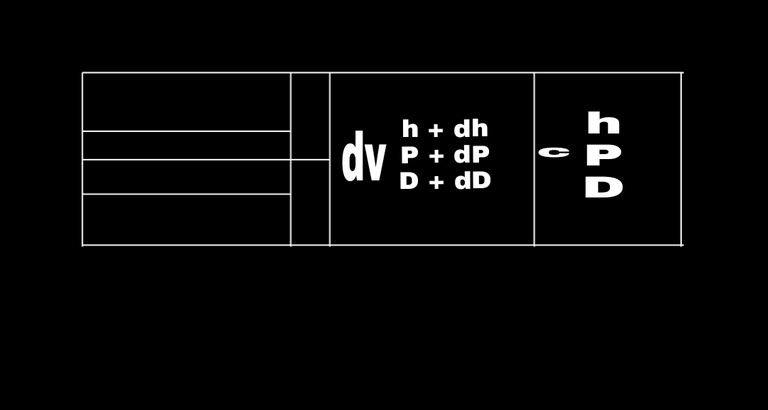
Photo credit: Created using mobile AUTO CAD APP.

---

c = (KRT)^1/2

where ;

k = Specific heat ratio

R = Gas constant of the specified gas

T = Temperature at that instant

D = density

P = Pressure

h = Entalpy

An imperative parameter in the investigation of compressible liquid flowis the Mach number Ma,named after the Austrian physicist Ernst Mach(1838– 1916). It is the proportion of the real speed of the liquid (or a question ingrain liquid) to the speed of sound in a similar liquid at a similar state:

Ma = V/c

where

V = speed of the liquid or particle in the liquid.

c = speed of sound in a similar liquid at a similar state.

Fluid flow regimes are often described in terms of the flow Mach number.The flow is called sonic when Ma = 1, subsonic when Ma < 1, supersonic when Ma > 1, hypersonic when Ma 》1,and transonic when Ma is approximately 1.

THE CONVERGING-DIVERGING NOZZLE

A de Laval spout also called converging-diverging nozzle(or focalized different spout, CD spout or con-di spout) is a tube that is squeezed in the center, making a precisely adjusted, topsy-turvy hourglass shape. It is utilized to quicken a hot, pressurized gas going through it to a higher supersonic speed in the hub (push) bearing, by changing over the warmth vitality of the stream into dynamic vitality. Along these lines, the spout is generally utilized as a part of a few sorts of steam turbines and rocket motor spouts. It additionally observes use in supersonic fly motors.
Comparable stream properties have been connected to fly streams inside astronomy.


Consider the subsonic move through a focalizing spout as appeared in Fig. below. The spout delta is appended to a supply at weight (Pr) and temperature (Tr). The repository is adequately vast with the goal that the spout channel speed is immaterial. Since the liquid speed in the store is zero and the move through the spout is approximated as isentropic, the stagnation weight and stagnation temperature of the liquid at any cross segment through the spout are equivalent to the supply weight and temperature, separately. Presently we start to decrease the back weight and watch the subsequent consequences for the weight dispersion along the length of the spout, as appeared in Fig. below. On the off chance that the back weight (Pb) is equivalent to (Pa), which is equivalent to (Pr), there is no stream and the weight circulation is uniform along the spout. At the point when the back weight is diminished to (Pb), the leave plane weight (Pe) additionally drops to (Pb). This makes the weight along the spout diminish in the stream bearing .

At the point when the back weight is lessened to (Pc) (P*, which is the pressure required to build the liquid speed to the speed of sound at the leave plane or throat), the mass stream achieves a most extreme esteem and the stream is said to be gagged or choked .Further decrease of the back strain to level (Pd) or underneath doesnt not bring about extra changes in the weight appropriation, or whatever else along the spout length.

---

I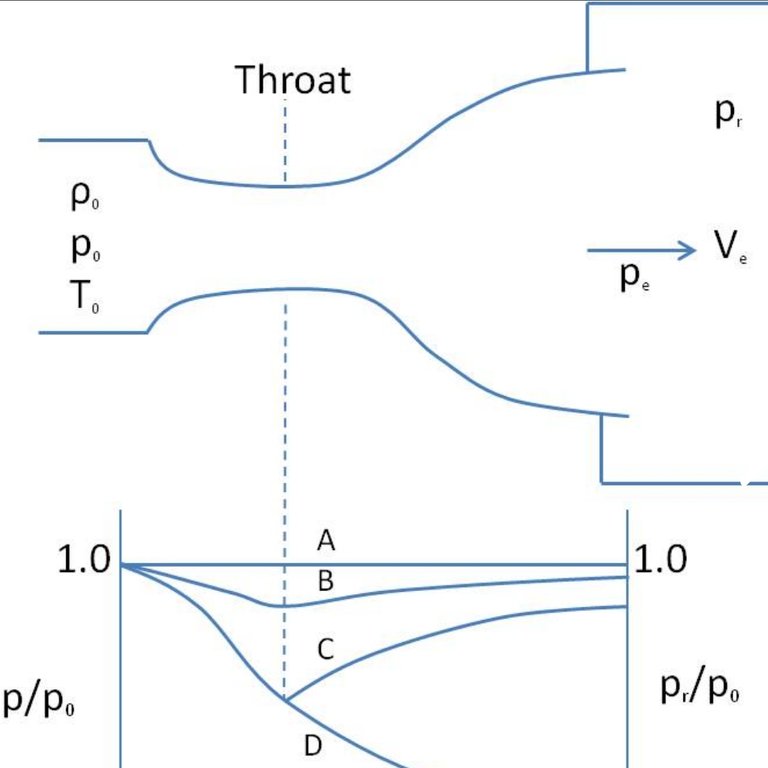

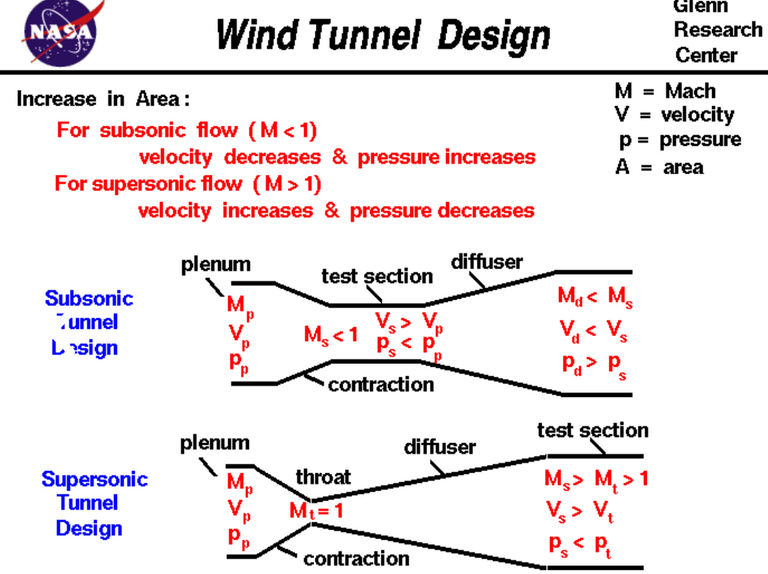
^{Wikimedia: A Converging-Diverging Nozzle}

---

^{Wikimedia(Nasa): DESIGN OF TUNNEL}

---

The rocket engine nozzle and turbine nozzle are shaped in the converging-diverging manner to obtain maximum thrust in supersonic Streams, it also finds its application in air transfer duct and also in flow duct.

---

^{Wikimedia: THE ROCKET NOZZLE}

---

REFERENCE

▪FLUID MECHANICS (fundamental and applications) By YUNUS .A. CENGEL & JOHN .M. CIMBALA

▪FLUID MECHANICS BY R.K. RAJPUT

▪CONVERGING-DIVERGING NOZZLE

^{Wikimedia(Nasa):WIKIPEDIA}

▪DESIGN OF CONVERGING-DIVERGING TUNNEL

^{Nation Aeronautics and Space Administration(NASA)}