[ESP]

¡Hola, estudiosa comunidad de Hive! 👋

En esta publicación, exploraremos los fundamentos de los sistemas de numeración que son cruciales en el mundo de la informática y la electrónica digital: el binario, el octal y el hexadecimal. Estos sistemas son esenciales para entender cómo las computadoras procesan y representan datos. 📚🔢

¿Qué son los Sistemas de Numeración? 🤔

Los sistemas de numeración son métodos para representar números. En electrónica y computación, además del sistema decimal común, utilizamos sistemas que se basan en diferentes bases, como la base 2 (binario), base 8 (octal) y base 16 (hexadecimal).

Sistemas Principales 📊

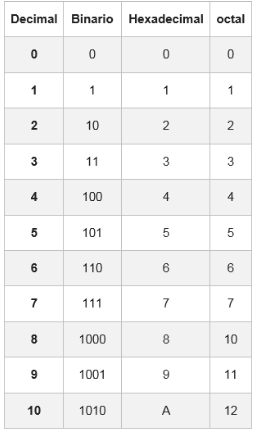
• Binario (Base 2): Utiliza solo dos dígitos, 0 y 1. Cada dígito en un número binario es un bit, y es la base de la operación de todas las computadoras modernas.

• Octal (Base 8): Utiliza los dígitos del 0 al 7. Fue muy utilizado en los primeros días de la computación porque es más fácil de convertir a binario que el decimal.

• Hexadecimal (Base 16): Utiliza los dígitos del 0 al 9 y las letras de la A a la F para representar los valores del 10 al 15. Es extremadamente útil en informática porque una sola cifra hexadecimal puede representar cuatro bits, lo que simplifica la representación de números binarios largos.
  

Importancia de estos Sistemas 🌟

• Simplificación y Eficiencia: Facilitan la representación y manipulación de grandes cantidades de datos binarios, simplificando el diseño de hardware y software.
• Interoperabilidad: Permiten a los ingenieros y programadores convertir y manejar datos entre diferentes sistemas y plataformas de manera eficiente.
• Optimización de Recursos: Ayudan a reducir el espacio y la complejidad en la programación y el almacenamiento de datos.

Ejemplo Práctico: Uso en Programación 🎛️

• Binario: Directamente utilizado en la programación a nivel de máquina y para operaciones lógicas.
• Octal: A menudo se usa en sistemas Unix y Linux para establecer permisos de archivos.
• Hexadecimal: Ampliamente utilizado en programación para definir colores en CSS, direcciones de memoria y en el desarrollo de interfaces de hardware.

---

---

📢 ¡Gracias por explorar los sistemas de numeración conmigo! 📘

Espero que esta introducción te haya proporcionado una visión clara de cómo y por qué utilizamos diferentes sistemas de numeración en tecnología. Si tienes preguntas o deseas compartir cómo utilizas estos sistemas en tus proyectos, por favor, comenta abajo. 📝

🔔 Mantente sintonizado para más temas técnicos que profundizan en los fundamentos de la informática y la electrónica. 🌐

🤝 Únete a la conversación en redes sociales para más intercambios y aprendizajes. Tu participación enriquece nuestro conocimiento colectivo. 💬

📷 Comparte tus proyectos: Si has trabajado con sistemas numéricos en tus desarrollos, ¡nos encantaría verlos! 🛠️

🌟 Sigue activo en la comunidad: No olvides seguir esta cuenta para obtener contenido continuo que te inspirará y ayudará en tus aventuras tecnológicas. 🚀✨

¡Hasta la próxima, sigue aprendiendo, compartiendo y creando!

---

---

---

[ENG]

Hello, fellow Hive community! 👋

In this post, we'll explore the fundamentals of numbering systems that are crucial in the world of computing and digital electronics: binary, octal, and hexadecimal. These systems are essential to understanding how computers process and represent data. 📚🔢

What are Number Systems? 🤔

Numbering systems are methods of representing numbers. In electronics and computing, in addition to the common decimal system, we use systems that are based on different bases, such as base 2 (binary), base 8 (octal), and base 16 (hexadecimal).

Major Systems 📊

• Binary (Base 2): Uses only two digits, 0 and 1. Each digit in a binary number is a bit, and is the basis of operation for all modern computers.

• Octal (Base 8): Uses the digits 0 through 7. It was widely used in the early days of computing because it is easier to convert to binary than decimal.

• Hexadecimal (Base 16): Uses the digits 0 through 9 and the letters A through F to represent the values ​​10 through 15. It is extremely useful in computing because a single hexadecimal digit can represent four bits, which simplifies the representation of long binary numbers.
  

Importance of these Systems 🌟

• Simplification and Efficiency: They facilitate the representation and manipulation of large amounts of binary data, simplifying the design of hardware and software.
• Interoperability: They allow engineers and programmers to efficiently convert and handle data between different systems and platforms.
• Resource Optimization: They help reduce space and complexity in programming and data storage.

Practical Example: Use in Programming 🎛️

• Binary: Directly used in machine-level programming and for logical operations.
• Octal: Often used in Unix and Linux systems to set file permissions.
• Hexadecimal: Widely used in programming to define colors in CSS, memory addresses, and in hardware interface development.

---

---

📢 Thanks for exploring number systems with me! 📘

I hope this introduction has given you a clear view of how and why we use different number systems in technology. If you have questions or would like to share how you use these systems in your projects, please comment below. 📝

🔔 Stay tuned for more technical topics that delve deeper into the fundamentals of computer science and electronics. 🌐

🤝 Join the conversation on social media for more sharing and learning. Your participation enriches our collective knowledge. 💬

📷 Share your projects: If you have worked with number systems in your developments, we would love to see them! 🛠️

🌟 Stay active in the community: Don't forget to follow this account for ongoing content that will inspire and help you in your tech adventures. 🚀✨

Until next time, keep learning, sharing, and creating!