En el artículo anterior se demostró que el poder de voto en Steemit decrece según las siguientes fórmulas

Utilizando estas expresiones se demostró que un usuario que vote n veces diarias en un corto periodo de tiempo verá como su poder de voto luego de transcurrir 24 horas tras haber votado tiende a un valor V0, es decir, un punto de equilibrio y dicho valor viene dado por la siguiente expresión:
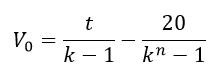
Sustituyendo los valores de t y k se obtiene
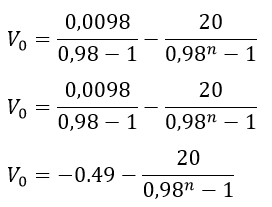
Reordenando
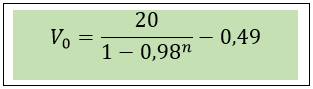
Fórmula para calcular el punto de equilibrio del poder de voto luego de n votos --- Fuente: Elaboración propia
Con esta fórmula se puede calcular el punto de equilibrio V0 al que tenderá el poder de voto diario inicial de un usuario que vota diariamente n veces, por ejemplo si un usuario vota 11 veces al día
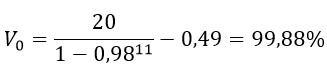
Su poder de voto al recargarse luego de 24 horas se aproximará a 99,88% (casi 100%), por lo tanto estará en un estado óptimo para apoyar con mayores recompensas al momento de votar, si se sustituye n por 10 o menos la fórmula arroja un valor superior a 100% lo cual no tiene sentido por lo tanto podemos concluir que el valor de n debe ser mayor que 10 para poder aplicar la fórmula del punto de equilibrio, sin embargo, aún queda la pregunta ¿Es posible obtener una recompensa mayor votando más veces aunque se devalúe el poder de voto?, para responder esta pregunta se debe calcular la sumatoria de todas las recompensas obtenidas al día, un usuario que vote con un poder de voto inicial de V0 recibirá en su primer voto la siguiente recompensa:

Debido a que se está modelando en función del poder de voto, se considerará a todos los demás factores como una constante con un único valor de C, de esta forma se puede apreciar cómo influye el poder de voto en las recompensas totales.
Para un usuario que vota una vez se cumple
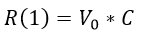
Para un usuario que vota 2 veces su recompensa total es igual a la recompensa anterior más la suma de la nueva recompensa, es decir
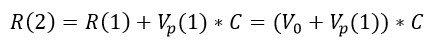
Sustituyendo
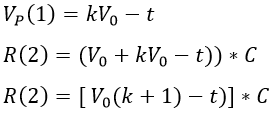
Para un usuario que vota 3 veces su recompensa total es
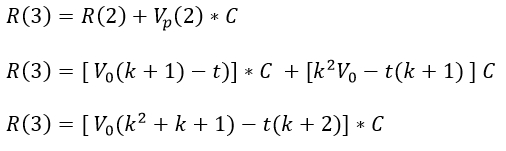
Para un usuario que vota 4 veces su recompensa total es
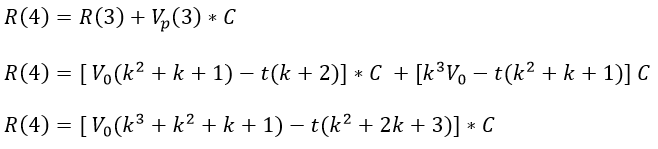
Y generalizando, para un usuario que vota n veces su recompensa total es igual a
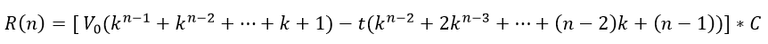
La primera serie de esta fórmula
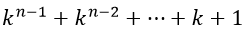
Puede expresarse también como
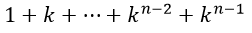
La cual es una progresión geométrica de n términos donde
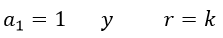
La fórmula para calcular la sumatoria de los términos de una serie geométrica finita es la siguiente:
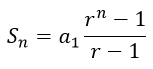
Aplicada a la serie anterior se obtiene
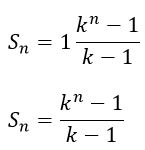
En cuanto a la segunda serie se simplifica teniendo en cuenta la siguiente multiplicación
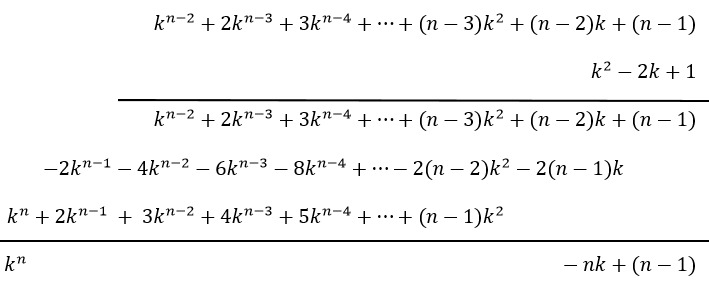
En base a este producto se concluye que
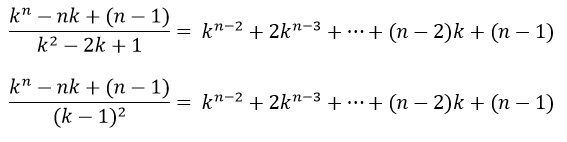
Sustituyendo los resultados para ambas series se obtiene
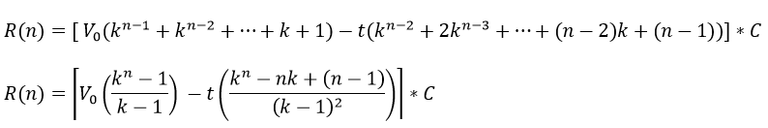
Esta fórmula permite calcular la suma de todas las recompensas obtenidas al votar n veces con un poder de voto inicial V0 asumiendo que los demás factores que intervienen en la curación son constantes, si el usuario vota la misma cantidad de veces todos los días su poder de voto se encontraría en uno de los puntos de equilibrio que vienen dados por la fórmula:
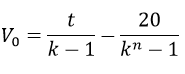
Sustituyendo en la expresión original
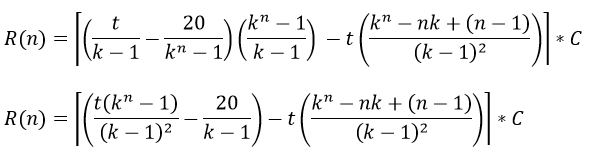
Aplicando factor común -t/(k-1)2
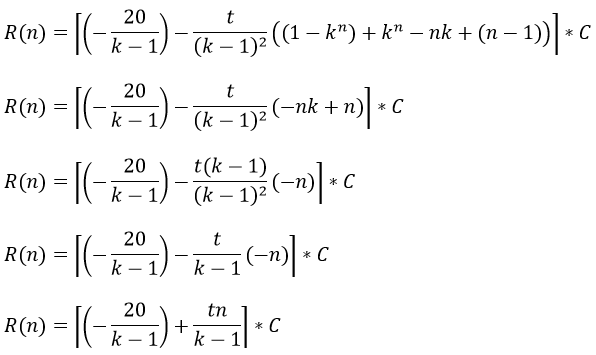
Reordenando se llega a la fórmula general de la sumatoria de las recompensa luego de haber votado n veces
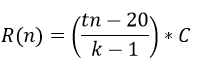
Sustituyendo k=0,98 y t=0,0098
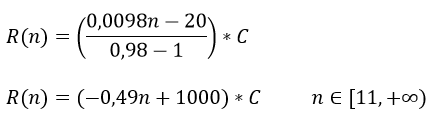
Esta es la función que permite calcular el total de las recompensas de curación obtenidas de acuerdo al número de votos diarios, asumiendo la misma cantidad de votos diarios y los demás factores que intervienen en la curación como una constante C positiva. Es evidente que esta función alcanza su valor máximo en n=11 siendo este el número de votos que maximiza las recompensas de curación
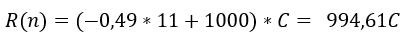
Para el caso de 10 votos diarios, la fórmula no puede aplicarse directamente debido a que la fórmula del punto de equilibrio genera valores del poder de voto superiores a 100%, sin embargo, se puede construir una tabla del decrecimiento del poder de voto a partir de 100% y realizar la sumatoria de dichos valores para encontrar el valor buscado
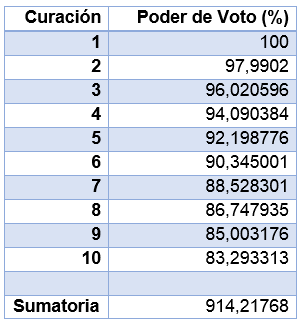
Tabla N° 1- Recompensa obtenida al realizar 10 curaciones a partir de 100% de Vp --- Fuente: Elaboración propia
Por lo tanto R(10)=914,21768*C, como R(11)>R(10) es más rentable votar 11 veces al día con el objetivo de obtener mayores recompensas por curación. En base a los resultados obtenidos se concluye que para maximizar las recompensas de curación y mantener casi al 100% el poder de voto, se debe votar 11 veces al día, este hecho no es fortuito, los programadores debieron tener esto en cuenta al desarrollar Steemit con el fin de limitar la tasa de abusos mediante penalizar indirectamente el exceso de upvotes.

This is a test comment, notify @kryzsec on discord if there are any errors please.
Siendo un SteemStem Estados
Como siempre tus post son interesantes y muy útiles, no me sorprende elgrado de conocimiento y pasión hacia las matemáticas y el trabajo en steemit.
De nuevo un análisis muy detallado.
Es importante mencionar que partiste de la premisa que los 11 votos se dieron todos al tiempo, es decir, que entre ellos no diste chance de regeneración del poder de votación.
En un comentario que te hice en el otro post, te mostré que en realidad sí podemos llegar a 10 votos con máxima efectividad, solo que se deben espaciar 2.4 horas para dar tiempo de regeneración.
De hecho, así funcionan los bidbots, ellos consumen y distribuyen el 100% de su voto cada 2.4 horas.
Hola tienes toda la razón, solo que lo analice desde la perspectiva de un usuario que se conecta y hace todos sus votos una vez al día, gracias por mejorar el análisis, considero bastante complicado votar cada 2,4 horas aunque claro en el caso de los bots es posible y en ese caso como se trata de 10 votos al 100% , la ecuación nos daría R(10)=10 * 100 * C = 1000C el cual es el valor máximo posible como bien indicas.
Brillante como siempre, muy fan de las demostraciones matemáticas
Gracias por el apoyo, Saludos.
Amigo @ydavgonzalez usa el tag "ciencia" y "matemáticas" también es valido, te lo digo porque así lo pueden observar una gran cantidad de lectores apasionados por los cálculos!
Impresionante! saludos!!
Ok, gracias por la sugerencia la tendré en cuenta.
Te esperamos en discord https://discord.gg/CPeCDwT
Excelente post amigo, si había escuchado de las recomendaciones de los 11 post al día pero no lo había visto tan bien fundamentado, gracias por compartirlo, te estoy siguiendo! Busco conocer más steemians que posteen contenido similar.
Gracias por el apoyo también puedes revisar mi post anterior en el cual se fundamenta el presente artículo:
https://steemit.com/stem-espanol/@ydavgonzalez/analisis-matematico-del-decrecimiento-del-poder-de-voto-en-steemit-por-que-votar-11-veces-al-dia
de una me paso a revisarlo, amigo donde te puedo contactar para hacerte un par de consultas?
Contactame por aquí:
Telegram: ydavgonzalez
Discord: ydavgonzalez#2680
El auxilio de las matemáticas es impresionante y en este caso mas aún ya que logras una demostración sin duda que llena de éxito a los lectores que le pongan atención. Los conocimientos expuestos aquí en estos cálculos aportan mucha alegría a cualquiera que pertenezca a steemit ya que le orienta en cuanto a la reputación, votos y ayuda que se puede ofrecer a otros del grupo. No tenía en verdad idea que pudiese determinar con tanta precisión los niveles de participación que a la larga que hacen crecer. La menor duda que pudiese haber existido en este asunto, pienso que queda disipada y totalmente motivadora . Queda pues que cada quien tenga presente esos consejos y a avanzar se ha dicho. Muchísimas Geacias y un gran saludo.
Gracias por el apoyo.
Saludos desde Venezuela.
Hola. Realmente no entendi. saludos
Hola te recomiendo leer este otro artículo que puede servirte de introducción y es un poco más sencillo:
https://steemit.com/stem-espanol/@ydavgonzalez/analisis-matematico-del-decrecimiento-del-poder-de-voto-en-steemit-por-que-votar-11-veces-al-dia
excelente tu trabajo @ydavgonzalez realmente me gustan las matemáticas y este tipo de trabajos.
Gracias por el apoyo.
Muy útil tu artículo. Saludos!
Gracias.
Muy interesante visión. Me encantó el análisis, perfectamente estructurado.
Que valiosa información, este tipo de artículos es muy bueno para aprender siempre un poco más sobre la plataforma. Gracias