En el caso que les acabo de mencionar se requieren de pruebas científicas (biológicas) para verificar la igualdad o semejanza entre 2 o más personas, pero cuando nos vamos al campo de las matemáticas el proceso se ve simplificado, ya que recurrimos a las herramientas de medición, ecuaciones y cálculos (aritmética y álgebra) para tener una referencia objetiva (medible y demostrable) de comparación.

Supongamos que tenemos 3 automóviles (como se ve en la siguiente representación gráfica), ¿podríamos realizar un análisis comparativo entre ellos?

A primera vista podría afirmar que el auto "A" es igual al auto "B", mientras que el carro "C" es más grande que los dos anteriores, a pesar que tiene la misma forma y color, por lo que me atrevería a decir que son semejantes. Sin embargo, esta descripción carece de las bases sólidas que sustenten mi afirmación, tal cual sucede con la comparación entre mellizos y gemelos, así que mejor tomaré mi cinta métrica y veremos una forma más creíble para el análisis.

Semejanza de las figuras: el automóvil "A" mide 35 líneas (al igual que el auto "B"), mientras que el automóvil "C" es el doble de la longitud, midiendo 70 líneas y teniendo una relación de semejanza de 2.

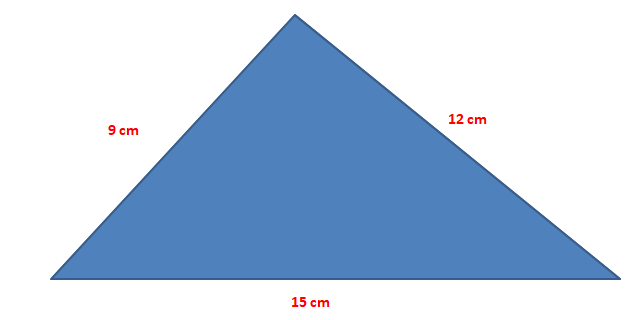
En Matemáticas existe una área relacionada con la Geometría y el estudio de las figuras geométricas, así que en adelante veremos un caso de semejanza entre triángulos y la representación del Teorema de Euclides que considera los términos de semejanza y proporcionalidad entre este tipo de figura geométrica.

Supongamos que tenemos un triángulo escaleno (sus 3 lados con longitudes diferentes) y conocemos algunas medidas de esos lados, podemos calcular la altura del triángulo usando las relaciones de proporcionalidad

Los 3 lados tienen longitudes distintas, para hallar la altura de este triángulo vamos a aplicar el Teorema de Euclides, el cual consiste en trazar esa línea vertical desde el vértice superior hasta dar origen a 2 triángulos rectángulos que guardan una relación de semejanza entre ellos, tal como vimos en el caso de los automóviles.

De esta manera, el triángulo original ΔABC será proporcional al ΔBCD y al ΔACD, por lo que podemos plantear las siguientes proporciones:

Sin embargo, no hemos resuelto nuestra incógnita inicial que es encontrar el valor de la altura del triángulo, es decir "h" o "CD". Si observamos la nomenclatura de los lados que hemos añadido al triángulo original, obtendremos otras relaciones de proporcionalidad relacionadas con los catetos del triángulo:

AB ∝ p+o = 15 cm = b (no indicado en el dibujo)

BC ∝ n = 12 cm

BD ∝ o = 15 cm − p

Las proporciones semejantes o equivalentes de estos 2 nuevos triángulos inscritos dentro del triángulo original son:

Como n = 12 cm y b = 15 cm, podemos calcular la longitud del segmento o lado "o" = 144 cm²/15 cm = 9,6 cm

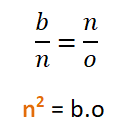
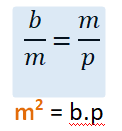
El lado "p" = m²/b = 81 cm²/15 cm = 5,4 cm. La base "b" del triángulo original ya ha sido dividido en 2 lados o = 9,6 cm y p = 5,4 cm

Finalmente, para el cálculo de la altura tomaremos en cuenta las proporciones de semejanza AC/CD

Para comprobar este resultado podemos aplicar el Teorema de Pitagoras considerando cualquiera de los 2 tríangulos internos:

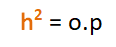
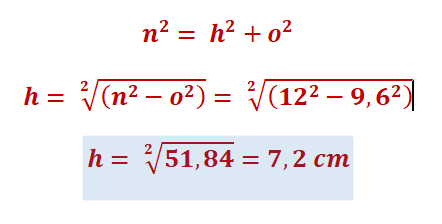
Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de GDJ: Portada "Teorema de Euclides"
• Blog Lifeder: Teorema de Euclides
• Wikipedia: Geometría