Diagrama de Venn
ProbabilidadesLa representación gráfica de los experimentos aleatorios comenzaron a usarse a mediados del siglo XIX y se expandió su aplicación gracias a los esfuerzos de John Venn de organizar una serie de datos en un solo conjunto que abarcara a todos los subconjuntos afines. Se estableció que los diagramas circulares o diagramas de Venn se emplearían para describir las relaciones entre objetos y los sucesos susceptibles que ocurran en un determinado ejercicio aleatorio.

El uso de una representación gráfica facilita la visualización del problema matemático y esquematiza los datos de una manera ordenada, agrupando los eventos por subconjuntos del universo probabilístico de posibilidades. Veamos un ejemplo salido de mi imaginario, cuando cursaba las materias humanistas, científicas y formación general, planteado de la siguiente manera:
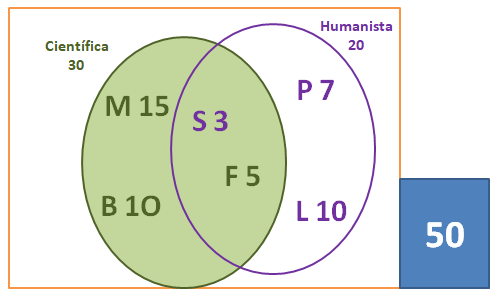
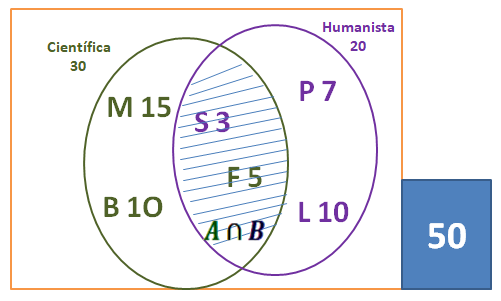
En la sección B, del cuarto año de bachillerato, hay 50 estudiantes que tienen predilección por algunas materias en específico: a 30 de ellos les encantan las materias científicas, 15 prefieren las Matemáticas, 10 Biología y 5 Física, mientras que otros 20 se maravillan con las materias humanísticas, a 7 estudiantes les gusta la Psicología, 3 se inclinan por Sociología y 10 por Lenguaje. Sin embargo, a los que les gusta la Física también tienen interés por la Sociología.

Sin secretos, inmediatamente realizamos la representación gráfica mediante el Diagrama de Venn, mostrado arriba, el cual desglosa la información suministrada. Incluimos las cantidades correspondientes a cada predilección por las materias científicas (30) y humanísticas (20) empleando los 2 círculos correspondientes, los enmarcamos dentro del conjunto (universo) de preferencias y a un lado señalamos el valor numérico del espacio muestral, que en este caso se corresponde con el número total de estudiantes del curso, esto es 50 estudiantes.
Si se selecciona un estudiante del curso y al azar, ¿cuál es la probabilidad de que le guste las Matemáticas?. Es muy relevante leer y entender el enunciado del problema matemático, razonar y aplicar la lógica para dar una respuesta acertada.
Un estudiante del curso involucra a los 50 estudiantes, todo el espacio muestral
La probabilidad de ocurrencia de un evento se determina mediante la Regla de Laplace:
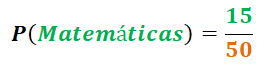

A pesar que el número de estudiantes que les gusta la Física se mantiene igual en 15, ahora el subconjunto de las materias científicas se reduce a 30 estudiantes dentro del espacio muestral de 50.¡Mucha atención!: si formulamos la pregunta de manera distinta, entonces se deben considerar otros valores numéricos, por ejemplo:Si se selecciona un estudiante al azar del grupo que les gusta las materias científicas, ¿cuál es la probabilidad de que le guste la Física?
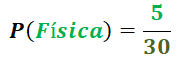
La probabilidad aumenta, P(Física) = 16,6%, tal como lo indiqué en mi anterior publicación, al reducirse el número de casos posibles hace que aumente la probabilidad (en porcentaje) de ocurrencia de un suceso o evento.
Ya para ir finalizando este artículo de enseñanza-aprendizaje, trataremos el punto de intersección de eventos aleatorios, formulando la siguiente interrogante:
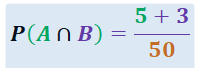
¡Matemáticas sin complejidades!
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de mohamed_hassan: Diagrama de Venn
- Blog: Diagramas de Venn, árbol y binomial
- Blog: Diagrama de Venn
- Artículo de Wikipedia: Diagrama de Venn
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a publicar en nuestra COMUNIDAD y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONOCER LOS DETALLES.
¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2023
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.