Funciones y Polinomios
Funciones polinómicas o Polinomios como funcionesEn el caso del cálculo algebraico debemos tener en consideración la presencia de un valor numérico llamado coeficiente, por ejemplo el 2, 657489890865454 o 4/5, cualquier número real (ℝ) que acompaña a la variable independiente, por ejemplo x, y, m, R, la parte literal de 1, 2, o n cantidad de letras y que pueden ser mayúsculas o minúsculas. Demás, estas variables pueden tener una potencia a la que se eleva la variable, por ejemplo m6 o T62830

Expresiones algebraicas:lo que acabo de explicar es la representación clásica de una expresión algebraica donde intervienen letras, números y símbolos aritméticos (suma, resta, división y multiplicación). Estamos acostumbrados a ver expresiones únicas como:6x3 donde el dígito 6 es el número o coeficiente que acompaña a la variable x, mientras que el 3 es el exponente de la variable.
Este tipo de expresiones algebraicas entran en la categoría de los polinomios, por ejemplo: 6x3 + 2x2
este es un polinomio de 2 términos, y la forma general para escribir un polinomio es de la forma:donde a es el coeficiente del primer término ax0, x es la variable independiente, mientras que el número sobre la x es el exponente. Se sabe que x0 = 1, todo número elevado al exponente 0 da como resultado la unidad, por lo que ax0 = a.1 = a sería el término independiente, porque no contiene a la variable x.
Polinomio:si nos basamos en las explicaciones anteriores, podemos aportar una definición para el polinomio, como una expresión algebraica que involucra letras y números, los cuales forman un conjunto de términos que se suman o restan para dar origen a una ecuación polinómica.P(X) = un polinomio de orden 5.
La idea es analizar una expresión polinómica, convertirla en una función polinomial y ver cuál es la representación gráfica que tienen esos polinomios.
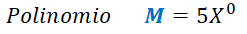
Este polinomio M puede ser tratado como una función polinómica cuando asignamos valores numéricos a la variable X:
Como ya lo había mencionado antes, X0 = 1, por lo que tendríamos un término independiente a = 5 para cualquier valor de la variable X.
El siguiente paso es crear una tabla de datos y graficar en el plano de coordenadas cartesianas las abscisas (valores de X) y las ordenadas (los números obtenidos al evaluar la función polinómica M(X)).
Veamos a ver qué sucede si el coeficiente de un segundo polinomio (N) es mayor que el del primer polinomio (M).
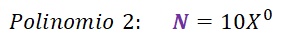
N(X) = 10X0
N(1) = 10(1)0 = 10
N(2) = 10(2)0 = 10
N(8) = 10(8)0 = 10
N(−1) = 10(−1)0 = 10
N(−6) = 10(−6)0 = 10
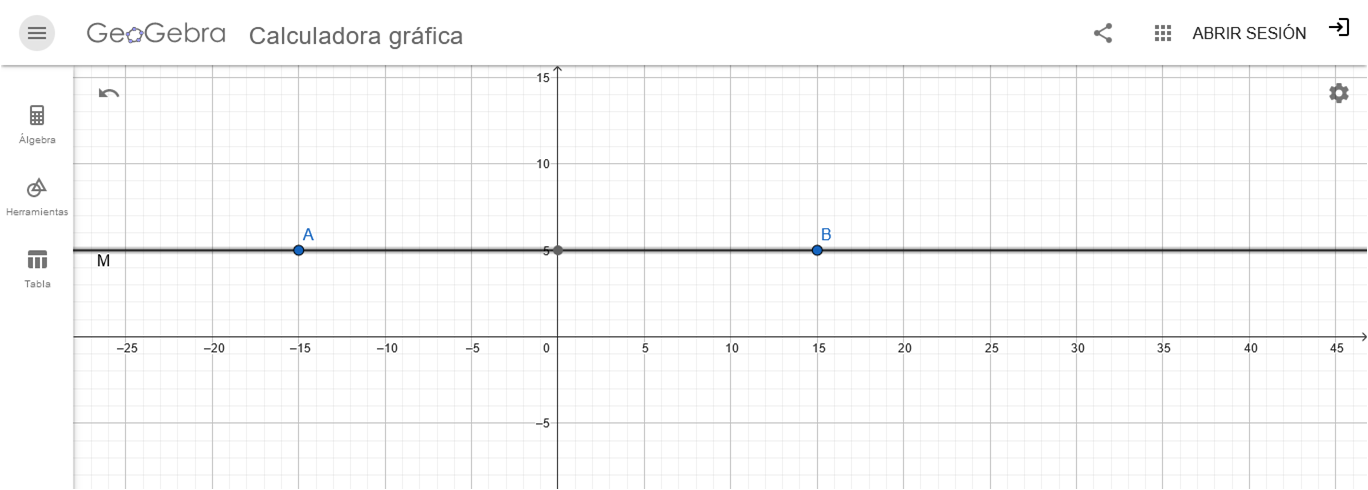
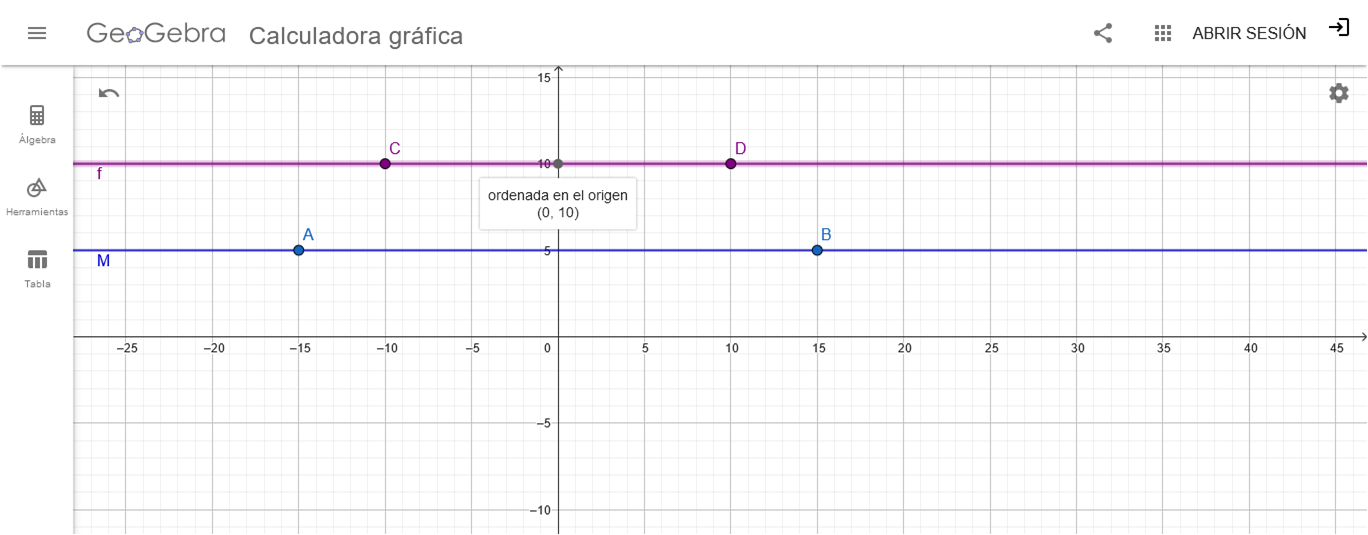
Precisamente el valor del término independiente es mayor, por lo que la gráfica de la función polinómica N(X) sigue siendo una línea horizontal, pero ubicada el el punto de la ordenada Y = 10 unidades.
Las Matemáticas constituyen una de las ciencias básicas que son fáciles de trabajar y entender, por lo que me limitaré a presentarles una de las características más versátiles de un polinomio de primer orden, relacionada con la ecuación de una línea recta y donde podemos encontrar el valor de la pendiente de una curva, tal como lo vimos en mi publicación más reciente.

R = 2X
Para evaluar este polinomio como una función debemos presentarlo como una función polinómica y asignarle los valores aleatorios a la variable X:
R(X) = 2X
R(X) = 2X
R(1) = 2(1) = 2
R(4) = 2(4) = 8
R(0) = 2(0) = 0
R(-2) = 2(-2) = -4
R(-10) = 2(-10) = -20
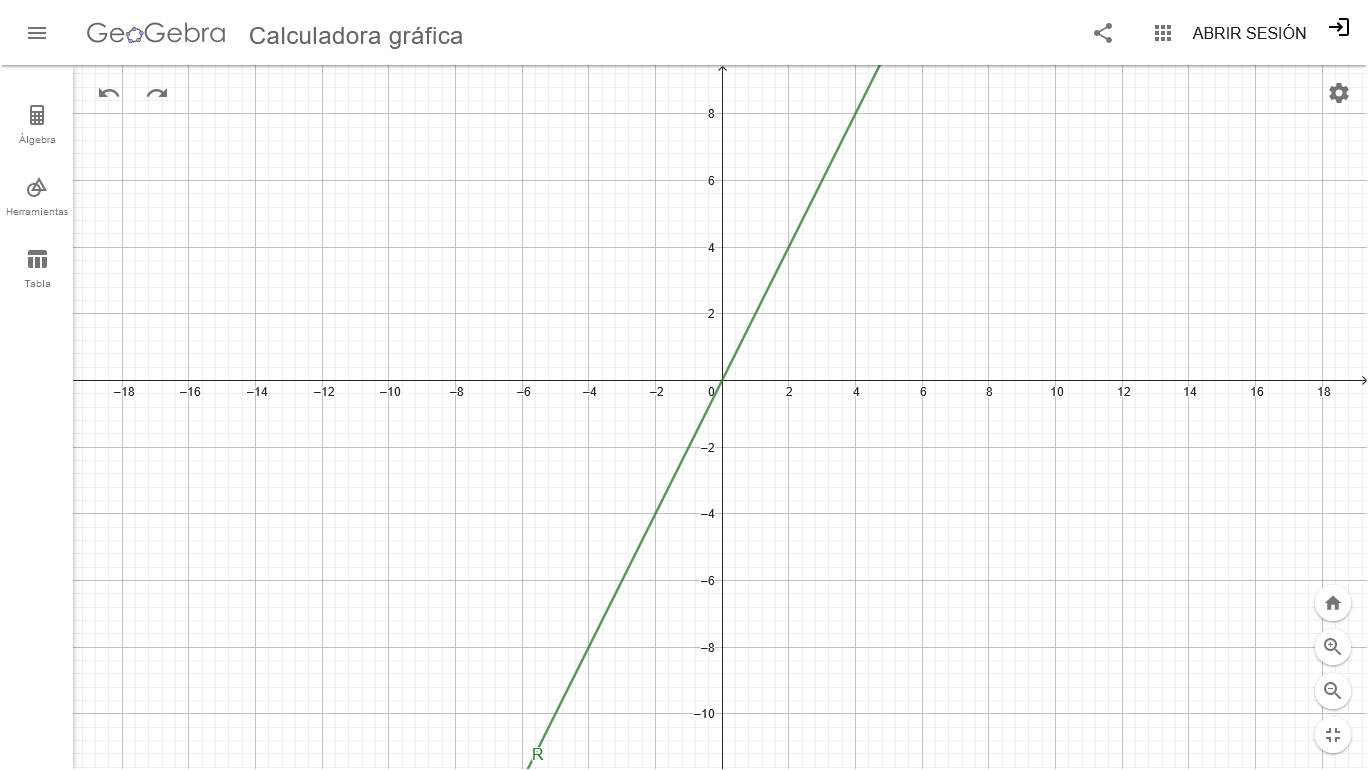
Construimos la tabla con las coordenadas cartesianas y graficamos:
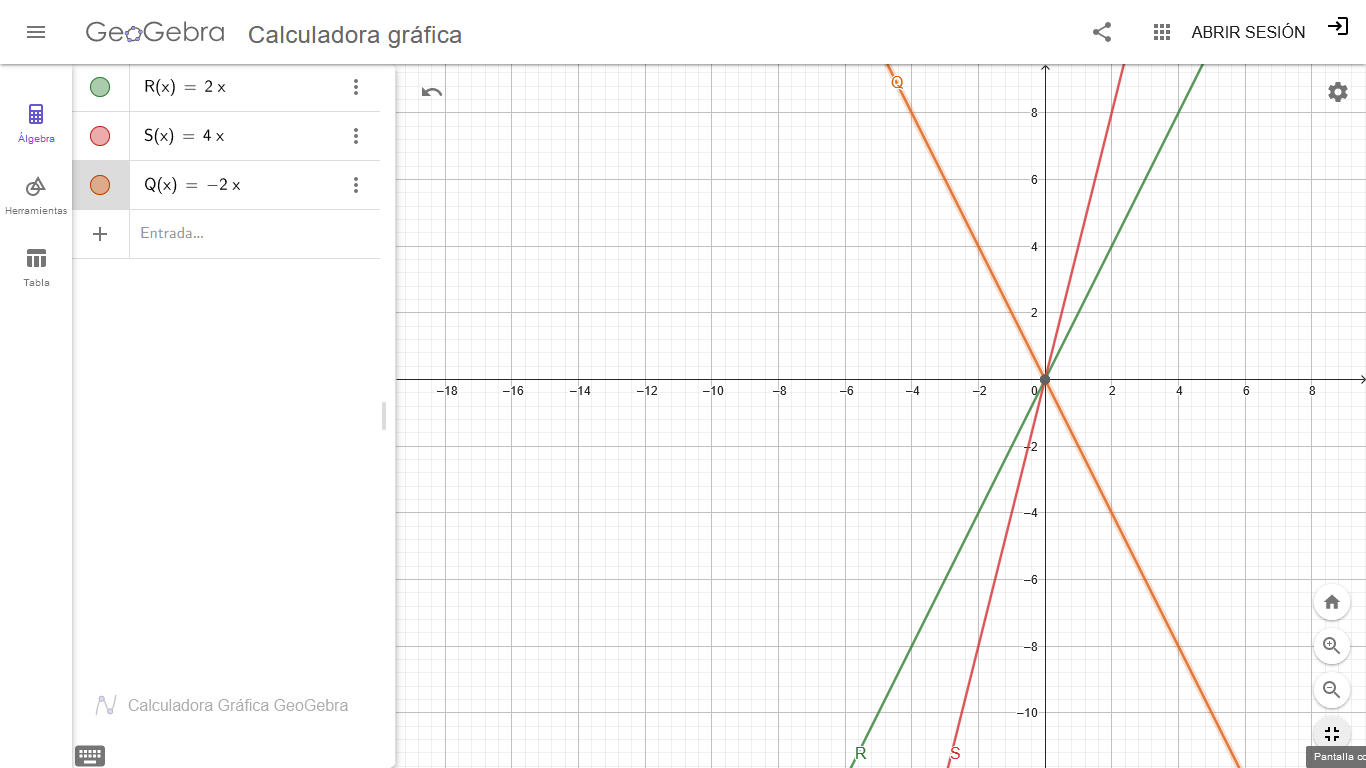
Es una línea recta que pasa por el origen, ya que el polinomio no tiene presente el término independiente que nos indicaría el punto de corte con el eje vertical (ordenada). Veamos qué sucede cuando el coeficiente del polinomio R(X) aumenta el doble y luego si ese coeficiente lo hacemos un valor negativo.
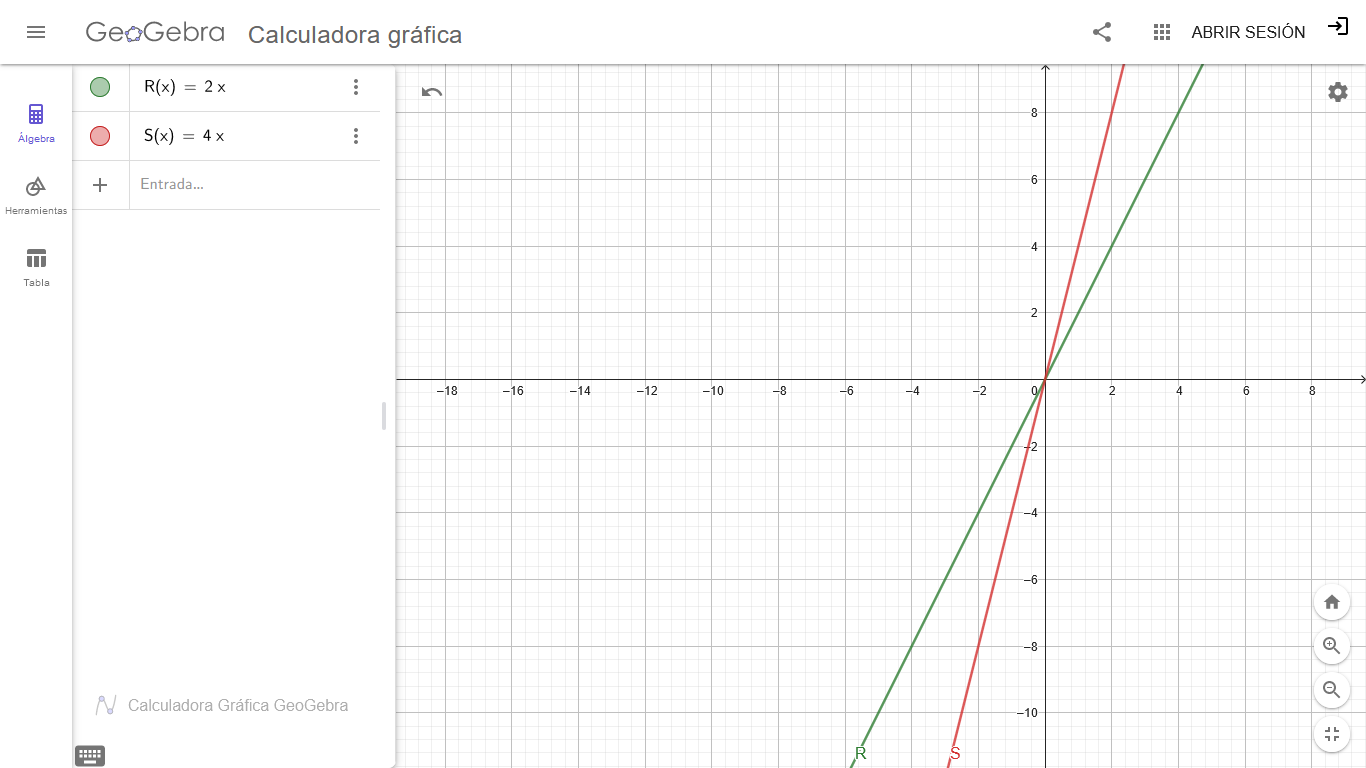
La gráfica de la nueva función polinómica S(X) = 4X, también es una línea recta que pasa por el origen, pero tiene una inclinación mayor que la función R(X), es decir que su pendiente es mayor. De aquí podemos deducir que el valor del coeficiente 4 está representando a la pendiente de dicha función polinómica.
Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad,
así que invariablemente encontraremos alguna solución
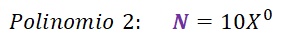


Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de mohamed_hassan: Funciones polinómicas
- Wikipedia: Polinomio
- Wikipedia: Ecuación algebraica
- Artículo de Wikipedia: Función polinómica
- Blog: Función polinómica
- Blog: Tipos de funciones
las variables de una igualdad,
así que invariablemente encontraremos alguna solución




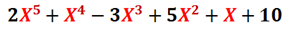
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.