Cálculo Diferencial
Interpretación Analítica y Geométrica de una DerivadaEl tema de las Derivadas forma parte de la transformación de una función continua de 1, 2 o más variables cambian su estado de manera extremadamente pequeña, muy parecido al estudio de las tendencias cuando una variable tiende a un número específico en los límites de una función. En este artículo veremos un ejemplo claro y sencillos del cálculo diferencial aplicado al volumen de un cilindro donde podemos tratar el caso de 1 o 2 variables, según asignemos valores al radio o la altura de este cuerpo geométrico.
En los planes de estudio a nivel de secundaria se analizan las figuras geométricas que pueden crear confusión si no se definen correctamente, como en el caso del aro, anillo o matemáticamente hablando, la corona circular, que tiene relación con una circunferencia más que con un círculo, el cual puede ser visualizado por el área de una moneda. Si colocamos unas 10 monedas apiladas una sobre la otra formaríamos un cuerpo geométrico conocido como cilindro.
En el caso de la corona circular, podemos notar que el centro es hueco, no hay sino un espacio vacío bordeado por una superficie límite que, aunque pueda ser muy delgada, posee un diámetro interno y uno externo, siendo esta la razón de llamarla "corona".
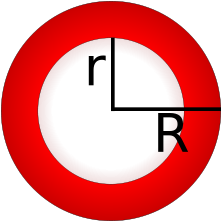
Note que para calcular el área de la corona circular (ACC) o del borde de color rojo es necesario considerar que: ACC = πR2 − πr2, mientras que las expresiones matemáticas para determinar el perímetro están dadas por: P(r) = 2πr y P(R) = 2πR, es decir el PT = P(r) + P(R). Hasta aquí no hay ningún secreto, nada de suposiciones y sin artilugios matemáticos!
En el caso de una moneda (M), el centro delimitado por la circunferencia, estaría lleno o cubierto por una superficie plana cuya área se puede determinar sin ningún problema mediante la relación, AM = πrM2
Volumen de otras formas geométricas
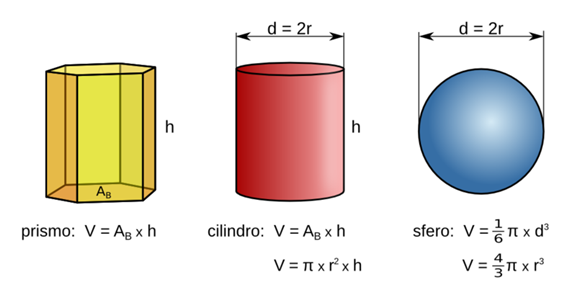
Como la base de un cilindro se asemeja o compara con una moneda, pues ya hemos determinado que el área de la base es: Abase = πr2 y como se trata de un cuerpo cilíndrico, debemos considerar su altura dada por "h". De esta manera, el volumen de un cilindro está dado por: Vc = πr2h, como se indica en la imagen anterior. Hasta aquí, nada nuevo, sólo una secuencia de términos geométricos y analíticos de algunas figuras geométricas que nos servirán para demostrar las variaciones infinitesimales de 1 o más variables en una función derivable, lo que aportaría mayor información que un simple cálculo algebraico, pues el análisis de las tendencias de la variable "radio" o la variable "altura" darán pie a la interpretación analítica relacionada con la relación de cambio del parámetro "volumen" con respecto a las variables "r" y "h".
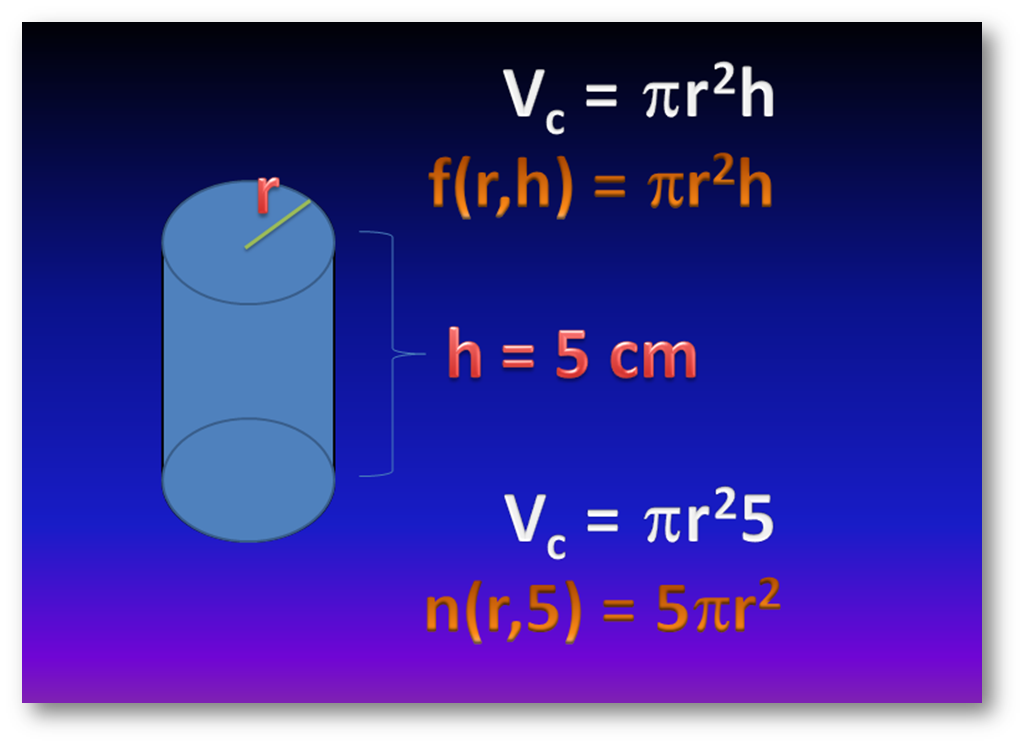
Es interesante detallar que las funciones f(r,h) y n(r,5), interpretan el análisis de la misma cantidad escalar Volumen, teniendo diferente imagen para distintos valores de los parámetros de entrada. Nosotros decidimos si realizamos el estudio con 1 o 2 variables según el nivel de detalle y precisión del "fenómeno" que analizamos. Veamos en qué nos afecta el cálculo diferencial y la información que podamos obtener de su interpretación analítica.

Como era de esperarse, a medida que se incrementan tanto "r" como "h", el volumen aumenta en una forma no lineal sino cuadrática debido al término "r2", y vemos una media parábola en la figura anterior. Ahora, para hacerlo de la manera más simple, pero más "inteligible" en lo posible, usaré el valor h = 5 cm para continuar con el análisis de tendencias hacia el límite de la función.
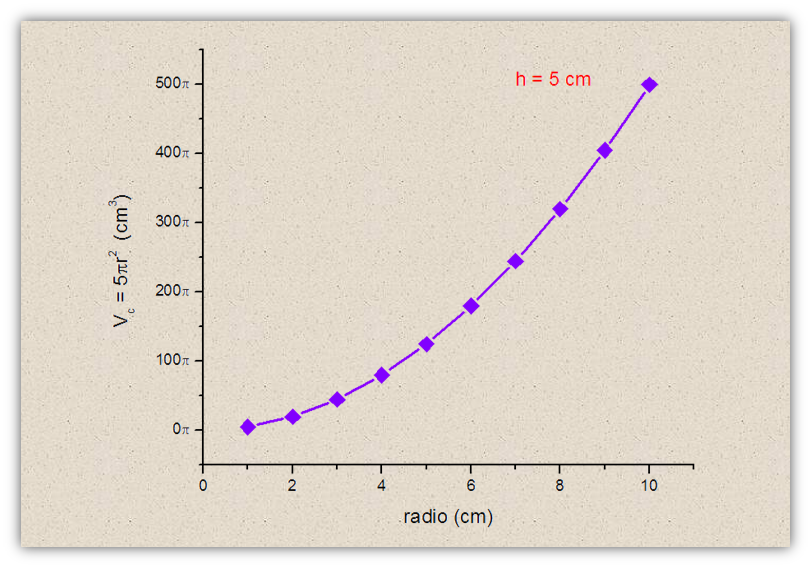

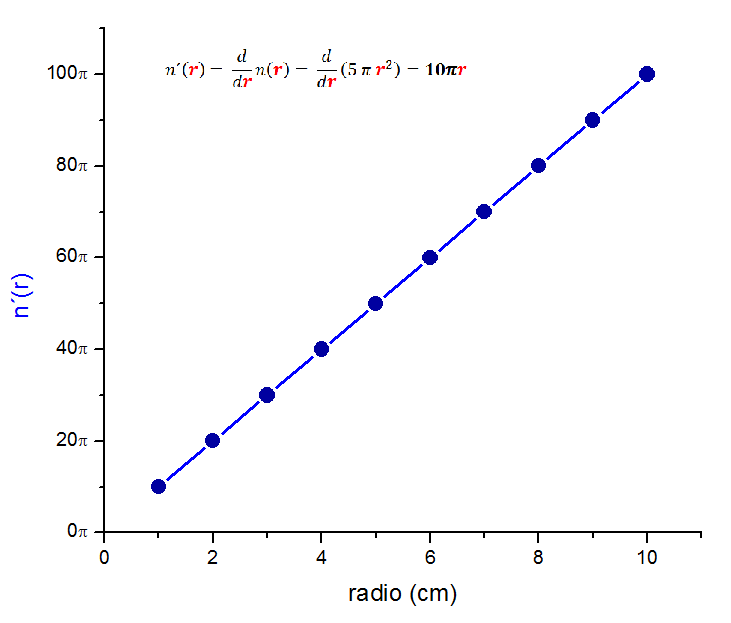
La interpretación analítica proporciona la información sobre la tasa de cambio del volumen respecto a la variable "r", por ejemplo si tomamos r = 2, entonces Vc = 20π. Esto se interpreta como que por cada cambio infinitesimal de "r" en (r, h) = (2, 5) el volumen cambiará en 20π.

Con agrado y satisfacción puedo exclamar ¡Voilà!
La interpretación de la derivada sigue siendo la pendiente de la línea tangente a la variación del volumen respecto al radio del cilindro, considerando la altura h = 5 cm como valor constante. Así se evidencia la conformidad entre la interpretación analítica y el significado geométrico al aplicar las reglas de derivadas en una función escalar.
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de geralt: Portada con fórmulas
- Wikipedia: Corona circular
- Imagen: Representación de un anillo
- gif de Lfahlberg: Longitud de un círculo
- Nota: Perímetro de un círculo
- Nota: Círculo
podemos hacer algunos cálculos básicos
con la derivación e integración entera de funciones escalares
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.