Los procesos de enseñanza y aprendizaje resultan muy complejos, aun más cuando las bases de esta interacción parten con la doctrina y capacitación del personal docente. Este comentario se aplica en los temas que tienen un componente real, referido a los números reales ℝ, sin que estén acompañados de unidades de medidas cuando forman parte del argumento de una función trigonométrica.

En muchas instituciones educativas se trabaja con el ángulo que forman dos rectas que se intersectan, expresando ese ángulo en grados (°), por ejemplo α = 25°. Nos enseñaron a usar un transportador de plásticos y calibrado con divisiones angulares desde 0° hasta 180° y otros llegan a medir hasta 360°. Sin embargo, el punto de partida para estudiar los ángulos y las funciones trigonométricas asociadas básicamente a un triángulo rectángulo (α = 90°) se inician con el establecimiento firme y sin ambigüedad de las unidades de medidas. Para esto se plantea el modelo de la circunferencia unitaria y se introduce el término de radián como la unidad de medida para los ángulos.

Las funciones trigonométricas admiten solamente números reales en su argumento, rigurosamente hablando no es correcto determinar el seno de 45° sen(45°). A partir de ahora debemos entender que los radianes son mediciones basadas en el radio de una circunferencia.

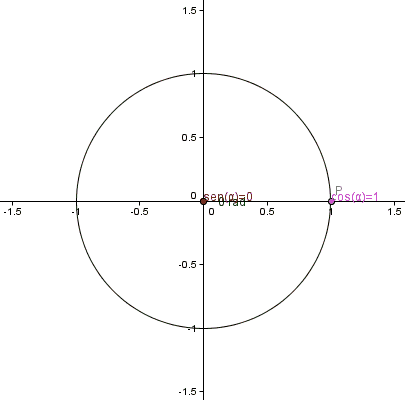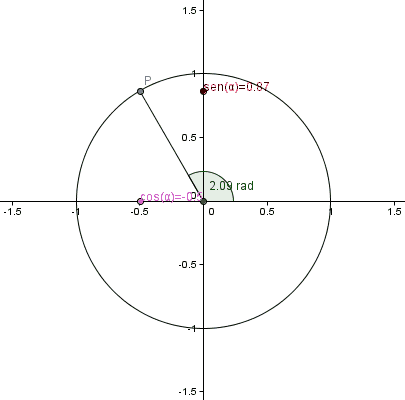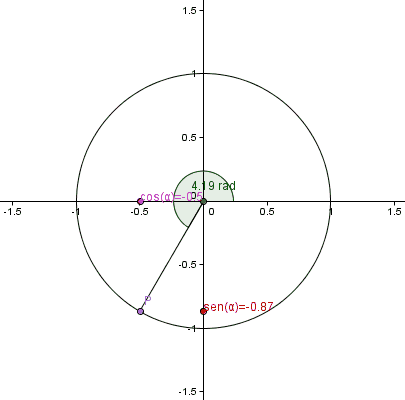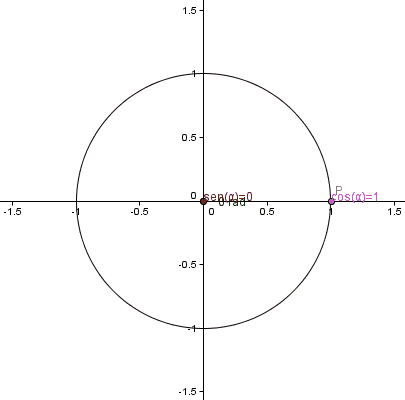
Medida del radio:

la distancia desde el punto medio de la circunferencia hasta el borde de la misma. Se proyecta esa longitud sobre el borde de la circunferencia y trazamos una recta desde el centro de la circunferencia hasta ese nuevo punto sobre el borde de la circunferencia. El ángulo medido desde el eje horizontal hasta la línea trazada corresponde a 1 radián. Cuando llegamos hasta el punto opuesto en la horizontal, comenzando desde el punto de partida, notamos que la distancia corresponde a 3 radianes y "algo más". El valor calculado y demostrado hasta la saciedad corresponde al valor de la constante π = 3,14159265358979....... (en forma abreviada π = 3,14159).

Así que en una máquina de funciones, debemos introducir el valor de la variable (parámetro α, correspondiente al número real del ángulo), se establece la función que debe evaluar nuestra máquina (Senα) y la procesa con los cálculos matemáticos respectivos (álgebra y aritmética). Finalmente, la máquina de funciones produce un resultado que es mostrado a los 3 espectadores que están atentos a ver el producto.

Note que ya hicimos la transformación de unidades de 3,14159 radianes a la constante π, que proyectado en la circunferencia corresponde a 180° (del sistema sexagesimal). Para ver la correspondencia de grados y radianes, basta realizar una regla de 3 simple y directa:

si 180° vale π

entonces

1° corresponde a π/180

90° equivalen a (90.π/180) = π/2

En concreto:

cuando la longitud del arco de circunferencia que dibujé en la imagen de portada, coincide con la medida numérica del radio de la circunferencia, entonces estaríamos definiendo la unidad de medida de los ángulos, es decir, el radián.

Existen otras metodologías para asignar los ángulos, hasta podemos crear una nueva unidad de medida, siempre partiendo del concepto de la circunferencia unitaria, por ejemplo si la circunferencia la vemos como una torta o pastel, podemos dividirla en 8 o 16 partes iguales, donde cada sección sería la unidad básica de medida (1 trozo, en lugar de 1 radián o 1°)

Apoyo bibliográfico y fuente de imágenes

• Imagen de geralt: Portada: El radián
• Wikipedia: Función trigonométrica
• Imagen de GDJ: Máquina industrial
• GIF de Lsdelrio: Funciones trigonométricas seno y coseno
• Wikipedia: Número π
• Blog TodaMateria: Funciones trigonométricas

¡Facilitemos el proceso enseñanza-aprendizaje!
Las unidades de medidas también son importantes
en las Matemáticas y buscan establecer las bases
estandarizadas que permitan resolver problemas, cuyos
resultados sean aceptadas en todo el mundo