Cordiales saludos mis Hive-Lectores, comunidad @stem-espanol y comunidad de Hive en general. Mis amigos Hive-Lectores, como ya he estado diciendo en mis posts anteriores, además de hacer llegar un poco de ciencia a la comunidad de Hive en general espero, con el presente contenido, seguir contribuyendo con la formación de aquellos estudiantes que por el COVID-19 deben seguir sus estudios en casa.
Después de haber indagado un poco en el campo de la Termodinámica en mis recientes posts anteriores, me adentro esta vez en el fascinante campo de la Mecánica Clásica Newtoniana. En la presente oportunidad les comparto el post que he titulado: MOVIMIENTO ARMONICO SIMPLE, UNA PRESENTACION DIDACTICA - Parte 1.
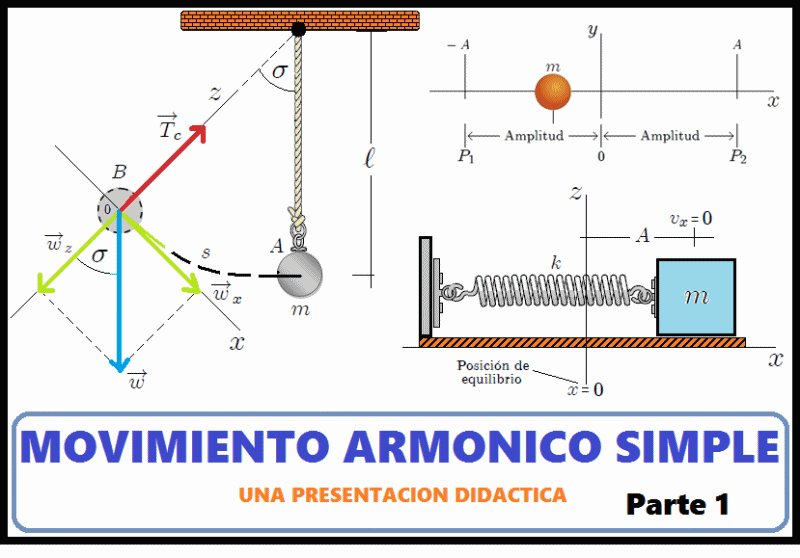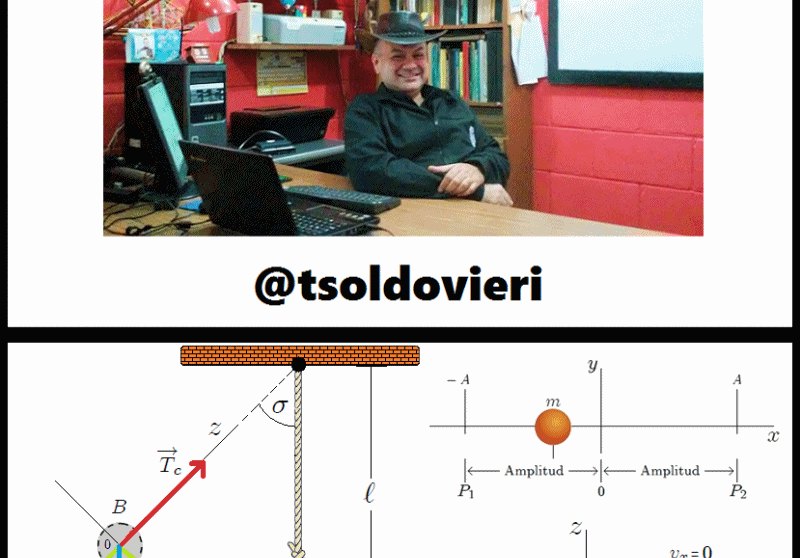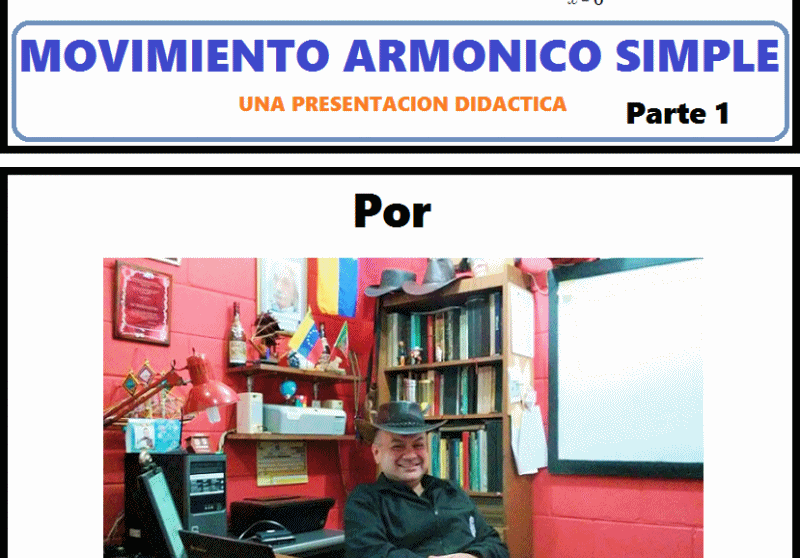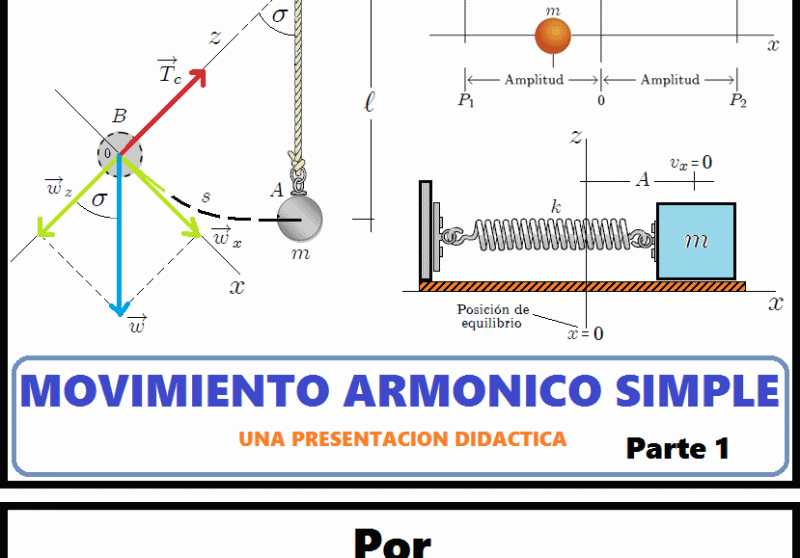
Mis estimados Hive-Lectores, como la gran mayoría de Ustedes lo sabe, la teoría relacionada con el Movimiento Armónico Simple (al cual me referiré como MAS de aquí en adelante) y su relación con el Movimiento Circular Uniforme (al cual me referiré como MCU de aquí en adelante) es fácil de encontrar en los numerosos textos de Física General que existen, sin embargo,
aquí haré una presentación acompañada con gifs animados y con la menor cantidad de contenido matemático posible, facilitando así el entendimiento del tema, haciéndolo muy fácil de asimilar. En varias oportunidades obviaré cálculos intermedios, que el lector podrá completar después de la lectura del presente contenido. |
|---|
El movimiento oscilatorio o vibratorio, mis estimados amigos Hive-Lectores, consiste en un movimiento repetitivo de un lado a otro realizado por un cuerpo alrededor de a una posición de equilibrio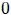 
, que es el punto donde se anula la sumatoria de las fuerzas actuantes sobre el cuerpo (y además se anula el torque resultante, si éste está presente). Es este tipo de movimiento, un Ciclo u Oscilación Completa consiste en el recorrido realizado en ir de una posición extrema a la otra y luego volver a la primera, pasando dos veces por la posición de equilibrio. Al número de ciclos por unidad de tiempo se le denomina Frecuencia 
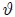. A la distancia alcanzada con respecto al punto de equilibrio y en el justo momento en que el movimiento cambia de sentido se denomina Amplitud 
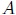. Este tipo de movimiento puede ser muy simple hasta llegar a ser muy complejo.
La forma más simple de movimiento oscilatorio está representada por el movimiento, libre de fricción (o que ha sido neutralizada de alguna manera), de un cuerpo (considerado como una partícula, es decir, de dimensiones despreciables) que vibra u oscila atrás y adelante, sobre la misma trayectoria y donde cada vibración toma la misma cantidad de tiempo. |
|---|
Este tipo particular de movimiento oscilatorio, mis estimados amigos Hive-Lectores, es el que describiré en el presente trabajo. A la cantidad de tiempo constante que emplea el cuerpo en realizar una oscilación completa se le denomina Período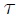 
, por lo cual suele llamársele Movimiento Periódico. La distancia desde el punto de equilibrio hasta cada extremo de la trayectoria es la misma en todo momento, es decir, la amplitud se mantiene constante.
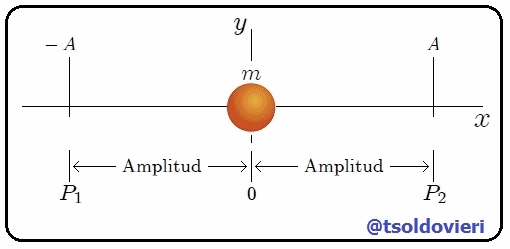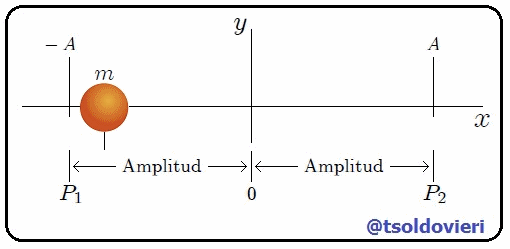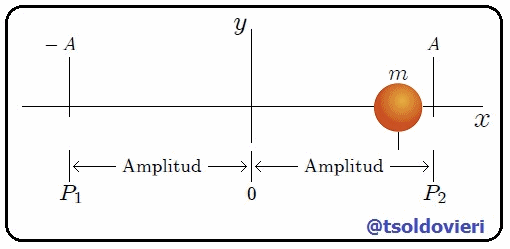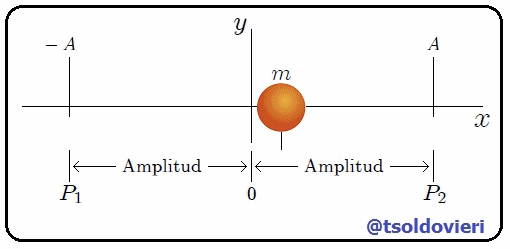
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
En la figura 1, mis amigos Hive-Lectores, les muestro una animación que representa el tipo de movimiento oscilatorio que mencioné antes. Se trata de un cuerpo (una partícula) de masa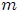 
que realiza un movimiento oscilatorio a lo largo del eje 
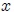, alrededor de una posición de equilibrio 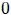y entre los puntos 
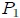y 
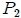. En caso de no existir fricción, como mencioné al principio, el movimiento no se detendría nunca y los puntos 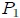y 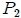estarían igualmente separados de 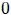. En caso de existir fricción (fuerza amortiguadora) el movimiento tendería a detenerse, mientras que las posiciones de 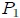y 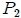con respecto a 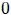serían distintas y tenderían a anularse.
El movimiento que anteriormente les describí, es reproducible si consideramos aplicada sobre el cuerpo una fuerza dependiente de la posición dada mediante,
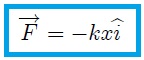
donde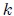 
es una constante positiva.
Animación realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape. Las imágenes son: By George Frederick Chambers - Public Domain - Fuente, By John Vanderbank - Public Domain - Fuente & De attributed to 'English School' - Bonhams - Dominio público - Fuente
Al aplicar la Segunda Ley de Newton, debida al Matemático y Físico británico Sir Isaac Newton (vean la figura 2), al Diagrama de Cuerpo Libre (DCL) de 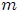(vean la figura 3) y después de pocos cálculos se obtiene fácilmente la ecuación diferencial de movimiento del cuerpo,
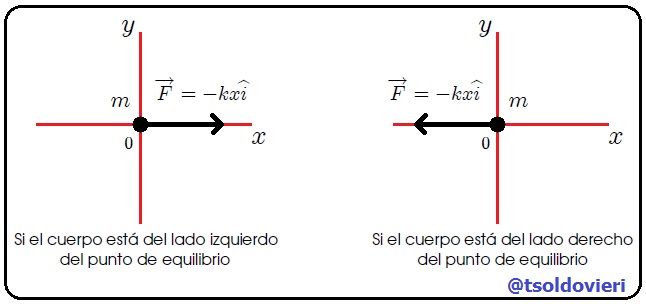
Realizada por mi persona, @tsoldovieri, usando la aplicación Paint
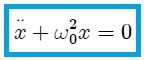
donde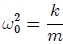 
y los dos puntos sobre la 
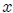indican segunda derivada total con respecto al tiempo 
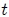, es decir, 
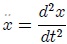. La solución de esta ecuación diferencial es bastante sencilla, resultando dos soluciones que vienen dadas por,
Debido a que las anteriores soluciones están presentes las funciones armónicas seno y coseno, se dice que el cuerpo realiza un MAS y al sistema que les mostré en la figura 1 se le denomina OSCILADOR ARMONICO SIMPLE. La cantidad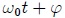 
se llama la Fase del Movimiento y la constante 
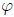se denomina Constante de Fase o Fase Inicial, que es un ángulo que será medido en radianes (rad). Más adelante, cuando les hable de la relación entre el MAS y el MCU, daré significado físico a 
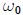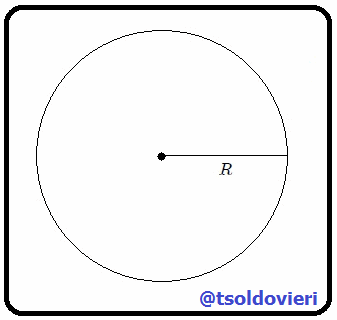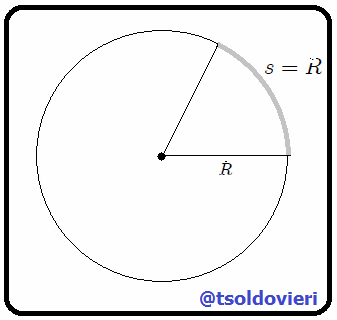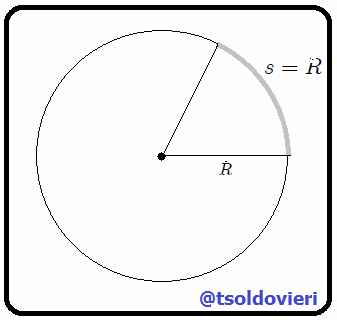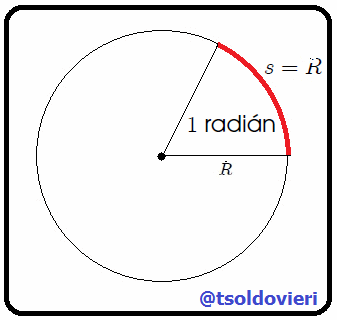
y a 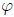. Se debe tener presente que Un Radián (rad) es la medida del ángulo que sustenta un arco cuya longitud 
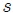es igual a su radio (vean la figura 4).
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
Diremos entonces, mis estimados amigos Hive-Lectores que, todo cuerpo cuya ecuación de movimiento venga dada por (2) realiza un MAS. |
|---|
Este movimiento recibe también el nombre de Oscilación Libre y debido a la inexistencia de fricción es tal que, una vez iniciado, no cesa nunca (como mencioné antes) manteniéndose constante su energía (de la que les hablaré más adelante) una vez establecida su amplitud. Por supuesto, se trata de una simplificación del caso físico real en el que las fuerzas disipativas o de rozamiento acabarían por extinguir finalmente el movimiento, desapareciendo las oscilaciones.
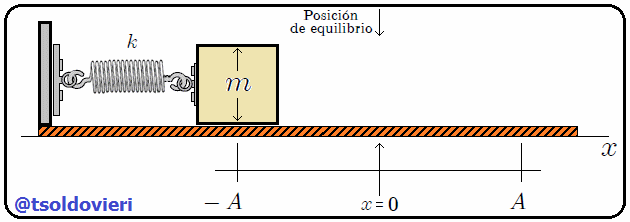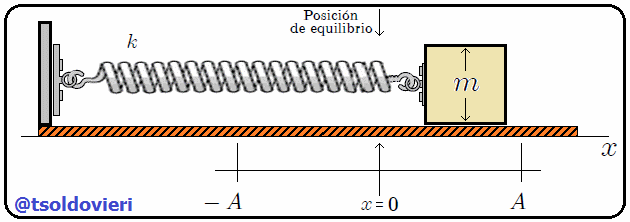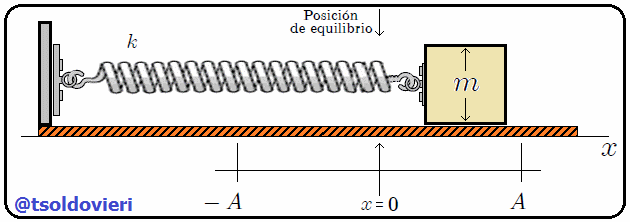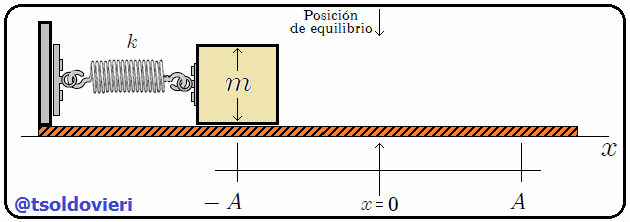
Supongamos (vean la animación de la figura 5), por ejemplo, que tenemos un sistema mecánico formado por un resorte y un cuerpo de masa 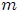(considerado como una partícula). El resorte está unido por su extremo izquierdo a un soporte fijo y por su extremo derecho al cuerpo, de tal manera que el cuerpo puede desplazarse sobre una superficie horizontal (el eje 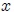) sin fricción.
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
Si hacemos que el cuerpo se desplace una pequeña cantidad 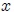con respecto a su posición de equilibrio 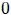(es decir, perturbamos el sistema), haciendo que el resorte se comprima o se estire, y después lo soltamos, se originará un MAS como les muestro en la figura 5. Lo anterior ocurre ya que los resortes responden a la denominada Ley de Hooke, debida al Físico y Astrónomo inglés Robert Hook 1660 (vean la figura 6) cuya expresión matemática es idéntica a (1). En este caso 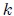representa la denominada Constante de Elasticidad del Resorte, la cual depende de las propiedades del material del que está construido el mismo. La fuerza 
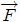representa la denominada Fuerza restauradora del Resorte. Debe tenerse presente que para que la ley de Hooke sea válida, el desplazamiento 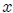debe ser pequeño. El DCL es el mismo que les muestro en la figura 3.
Autor desconocido - Dominio Público - Fuente
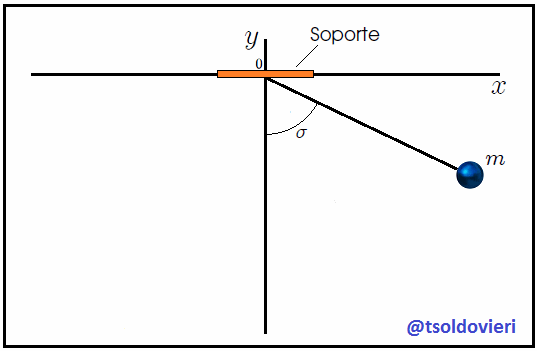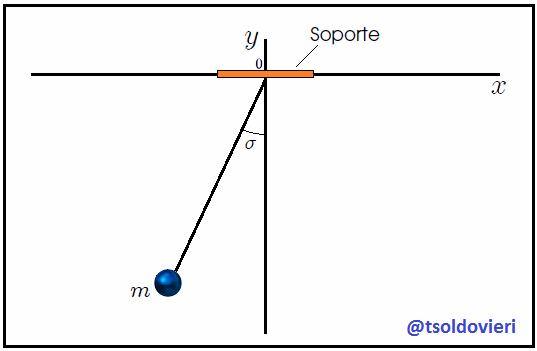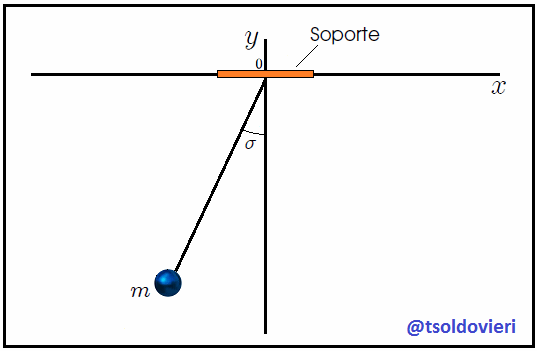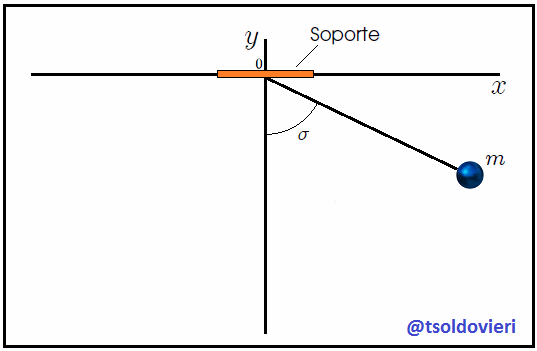
Veamos ahora, mis estimados amigos Hive lectores, el sistema que les muestro en la figura 7. Se trata de un Péndulo Simple, Péndulo Ideal o Péndulo Matemático, el cual es un sistema idealizado que consta de un cuerpo (considerado como una partícula) de masa 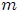(denominada Masa Pendular) suspendida de un soporte fijo mediante una cuerda de longitud 
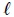, indeformable y de masa despreciable. Inicialmente la cuerda y la masa están en reposo a lo largo del eje 
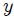(posición de equilibrio). Luego se perturba el sistema al desplazar la masa pendular de tal forma que la cuerda forme un pequeño ángulo 
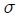con el eje 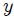. Finalmente se suelta.
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
Si al anterior sistema se le aplica la Segunda Ley de Newton se obtiene, después de el análisis del diagrama de cuerpo libre de la masa pendular (vean la figura 8) y unos pocos cálculos, la ecuación diferencial de movimiento que viene dada por la expresión,
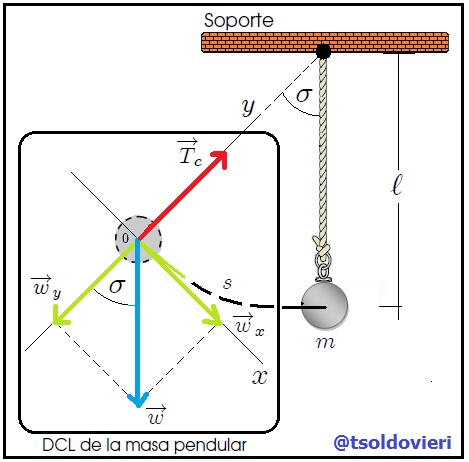
es la longitud del arco recorrido, 
es la tensión de la cuerda,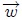 
el peso de la masa pendular y 
, 
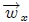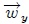sus componentesRealizada por mi persona, @tsoldovieri, usando las aplicaciones Paint y Word
donde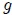 
es la aceleración debida a la gravedad y 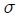es el ángulo (en radianes) formado entre la cuerda y el eje 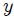. Como 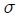es pequeño se tiene que 
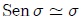, por lo tanto (4) se convierte en,
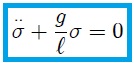
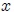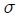Mis estimados Hive-Lectores, observen bien la anterior ecuación diferencial. Noten que es la misma ecuación (2), sólo que en este caso es y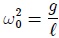 
. Por lo tanto, la masa pendular realiza un MAS.
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint, Word y PhotoScape
Finalmente, mis amigos Hive-Lectores, consideremos el sistema que les muestro en la figura 9. Se trata de un Péndulo Físico o Péndulo Compuesto que es cualquier cuerpo rígido (es decir, no es considerado como una partícula), de forma arbitraria y de masa 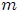, que puede oscilar libremente bajo la acción de su propio peso alrededor de un eje horizontal fijo (eje de giro), el cual pasa por un punto del cuerpo que no es su centro de masa. Debe tenerse presente que un Cuerpo Rígido o Sólido Rígido es aquel cuya forma no varía pese a ser sometido a la acción de fuerzas externas, lo cual supone que la distancia entre las diferentes partículas que lo conforman resulta invariable al transcurrir el tiempo.
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint, Word y PhotoScape
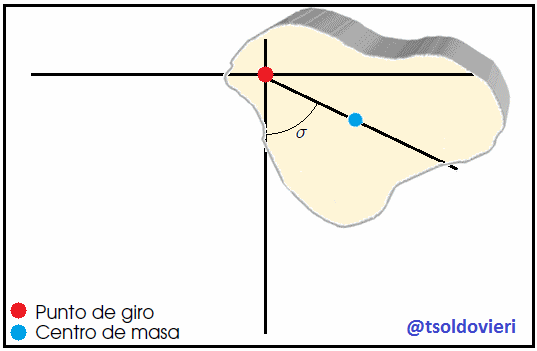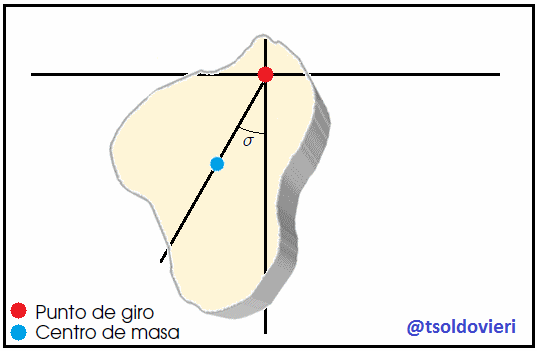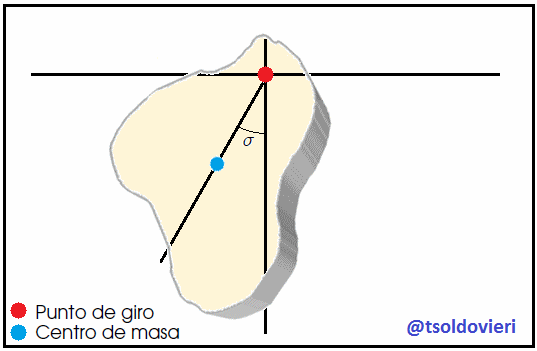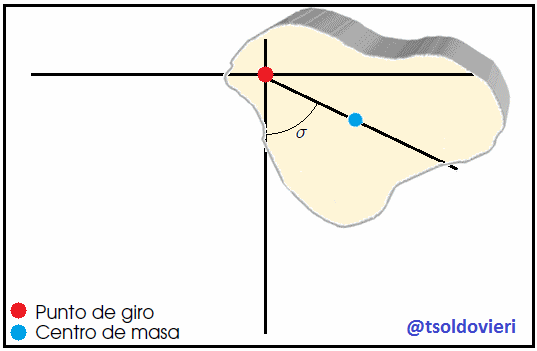
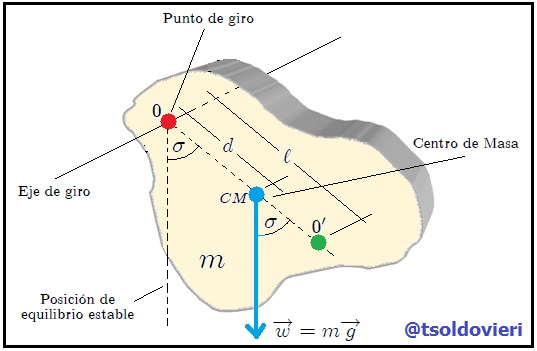
En la figura 10, mis amigos Hive-Lectores, les muestro el cuerpo irregular de la figura 9 en un instante dado de su movimiento fuera de la posición de equilibrio. se muestra un cuerpo irregular en esta situación. El peso 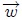crea un torque restaurador 
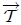con respecto al punto de suspensión 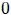(por donde pasa el eje de giro) dado por,
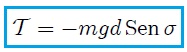
donde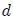 
es la posición del Centro de Masa 
con respecto al punto de giro situado en 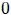. Por otro lado, como es sabido a partir de la Dinámica de un Cuerpo Rígido, el torque 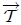viene dado mediante,
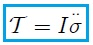
donde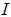 
es el Momento de Inercia del cuerpo y 
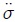su aceleración angular. Entonces, al igualar (6) y (7) resulta,
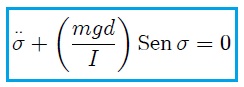
que es una ecuación diferencial de segundo orden del mismo tipo que (4), encontrada para el péndulo simple. Si se supone ahora desplazamientos angulares 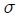pequeños, entonces es posible escribir que,
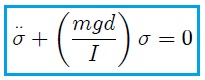
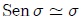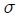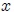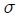puesto que para pequeño. La anterior ecuación es la Ecuación de Movimiento del Péndulo Físico. Mis estimados Hive-Lectores, observen bien la anterior ecuación diferencial. Noten que es la misma ecuación (2), sólo que en este caso es y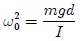 
. Por lo tanto, el cuerpo de la figura 9 realiza un MAS.
Existen más, y no pocos, ejemplos de sistemas que realizan MAS, entre ellos: el péndulo de torsión, el péndulo esférico, el pédulo cónico, etc. En fin, todo sistema cuya ecuación de movimiento sea de la forma (2) realizará un MAS.
En la segunda y última parte de este post les hablaré de la energía mecánica del OAS y de la relación existente entre éste y el Movimiento Circular Uniforme (MCU).
BIBLIOGRAFIA RECOMENDADA
Aquí les presento 7 textos que recomiendo si desean ahondar en el tema:
Soldovieri C., T. FISICA GENERAL - UNA INTRODUCCION A LOS FLUIDOS, VIBRACIONES Y TERMODINAMICA. Preprint, 2020. El borrador se puede descargar desde mi web personal: http://www.tsoldovieritsweb.ihostfull.com
Bauer, W. & Westfall, G. D. FISICA PARA INGENIERIA Y CIENCIAS, volume 1. McGraw-Hill/Interamericana de México, S. A. de C. V., 2011.
Bueche, F. J. & Hecht, E. FISICA GENERAL. Schaum. McGraW-Hill / Interamericana Editores, S.A. de C.V., México, 10ma edition, 2007.
Fishbane, P. M.; Gasiorowicz, S. G. & Thornton, S. T. PHYSICS FOR SCIENTISTS AND ENGINEERS WITH MODERN PHYSICS. Pearson Education Inc., 3th edition, 2005.
Burbano de E., S.; Burbano G., E. & Gracia M., C. FISICA GENERAL. Editorial Tébar, S.L., 2003.
Halliday, D.; Resnick, R. & Krane, K. S. FISICA, volume 2. Compañía Editorial Continental, S.A. de C.V., México, 4ta edition, 1994.
Hewitt, P. G. CONCEPTOS DE FISICA. Editorial Limusa, México, 1era edition, 1992.
Estimados amigos Hive-Lectores. Espero que la anterior información les sea de mucha utilidad. Si tienen preguntas, no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Igualmente, si tienen detalles que puedan nutrir o mejorar la anterior información, por favor, háganmelas saber. Hasta la siguiente parte del presente post ¡Saludos a todos! 😁.
LES INVITO VISITAR MI WEB PERSONAL www.tsoldovieritsweb.ihostfull.com
En esta página web podrás conseguir los borradores de los libros de texto que estoy escribiendo y varias listas de problemas con respuestas de: Optica, Mecánica Clásica, Mecánica Cuántica, Física General 1, Física General 2 y Física General 3. También encontrarás enlaces a otras páginas web de interés.
Deja tus comentarios en el libro de visitas! 😁
Saludos estimado @tsoldovieri. Muy buen material sobre este tipo de movimiento, ciertamente que la presentación del contenido acompañado de los gifs animados facilitan la comprensión del tema y sin duda resulta en un gran apoyo para los estudiantes que avanzan en sus clases con la modalidad a distancia.
Estimado @emiliomoron, así es, los gifs transmiten mucho de lo que con palabras sería dificultoso de transmitir. Muchas gracias por tomar un poco de tu tiempo para leer y comentar mi post. Cordiales saludos.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Thanks for the support @steemstem.
Un artículo impecable amigo @tsoldovieri, seguro estoy que será un material de mucha ayuda para aquellos estudiantes que reciben educación virtual, hacer de lo complejo algo fácil de entender tiene su merito, te felicito y seguimos en comunicación !
Gracias por seguir mis posts y por tus motivadores comentarios amigo @amestyj. Saludos cordiales.
Como siempre, un artículo lleno de imágenes animadas que complementan muy bien la teoría, esto me recuerda a una asignatura llamada "Tópicos de Física" que cursé en mis estudios. Buen trabajo, nos estamos leyendo ✅
Amigo @acont, gracias por convertirte en un continuo lector y comentador de mis post. Gracias por tu motivador comentario. Cordiales saludos.