¡Hola amigos de Hive Blog!
Reciban un cordial saludo.
En el estudio de los movimientos oscilatorios uno de vital importancia es el que describe un péndulo.
El movimiento oscilatorio descrito por un péndulo es observado en la naturaleza y en una gran variedad de sistemas mecánicos simples y complejos. Entre sus principales aplicaciones encontramos la medición del tiempo y la obtención del valor de la gravedad.
Para pequeñas oscilaciones, el movimiento oscilatorio del péndulo es análogo al descrito por un sistema masa-resorte, por lo que obedece a las mismas leyes matemáticas que gobiernan un movimiento armónico simple.
Dada su importancia, en este trabajo analizaremos los fundamentos físicos y matemáticos del movimiento oscilatorio de un péndulo simple y determinaremos el valor de la gravedad a partir de las variaciones que experimenta el periodo de oscilación ante los cambios de longitud.
Fundamentos teóricos
Un péndulo simple está formado por un hilo inextensible de longitud “L” y masa despreciable, que sujeta una masa puntual “m” que se balancea respecto a un punto fijo.
Cuando la masa es desplazada un ángulo “θmax” respecto de su posición de equilibrio “θ0=0”, las fuerzas actuantes obligarán al cuerpo a moverse en una trayectoria circular o arco en el que la masa esta confinada debido al hilo que la sujeta con una fuerza de tensión “T”.
En la siguiente imagen se muestra un diagrama de cuerpo libre en el que están representadas la tensión ejercida por el hilo y la fuerza gravitacional “mg” con sus respectivas componentes. La fuerza tangencial “mgsenθ” es la fuerza restauradora que siempre va dirigida hacia la posición de equilibrio "θ0=0" y es opuesta al desplazamiento.
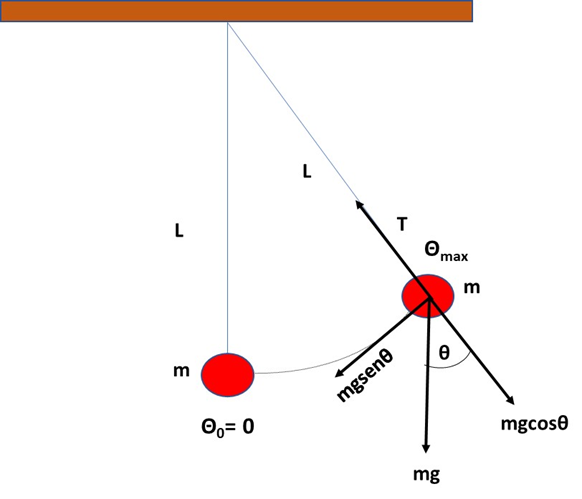
(Elaborada por @lorenzor en Powerpoint)
En la dirección tangencial tenemos de la segunda ley de Newton (∑Ft =mat) que:
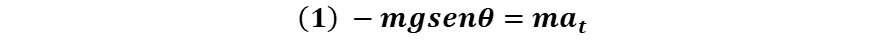
Donde la aceleración tangencial "at" está dada por el cambio de la magnitud de la velocidad "v", según lo expresa la siguiente ecuación:
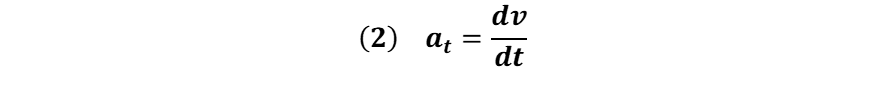
Para determinar el valor de la velocidad de la masa en la trayectoria circular o arco se debe obtener la derivada respecto al tiempo de dicho arco "s", el cual está dado por:
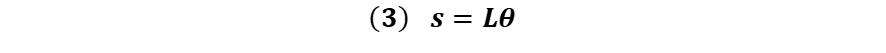
Diferenciando respecto al tiempo la expresión (3) tenemos:
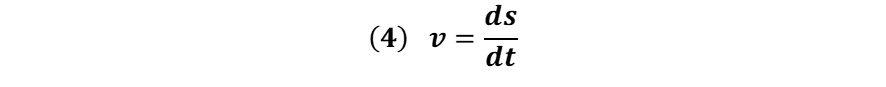
Sustituyendo (3) en (4) se tiene:
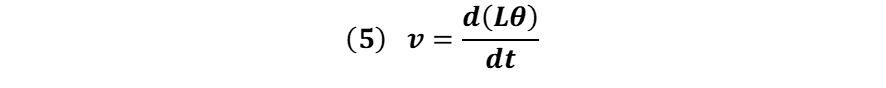
Dado que la longitud del hilo es constante se tiene que:
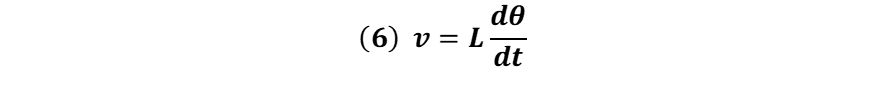
Sustituyendo (6) en (2), la aceleración tangencial queda expresada de la forma:
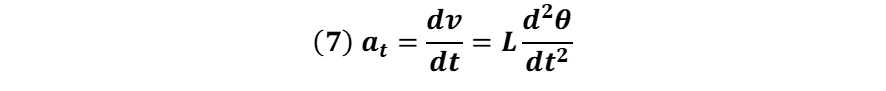
Reemplazando la ecuación (7) en (1) y simplificando obtenemos:
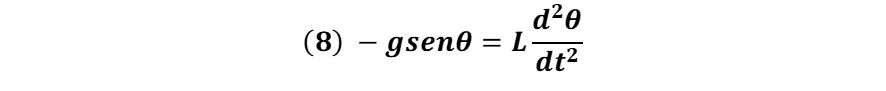
Para pequeñas oscilaciones (senθ ≈ θ)
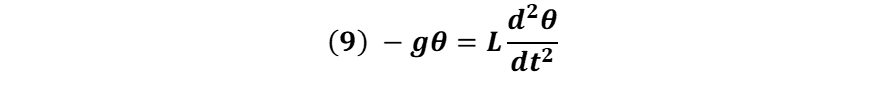
La ecuación diferencial dada por la expresión (9) se puede escribir de la forma:
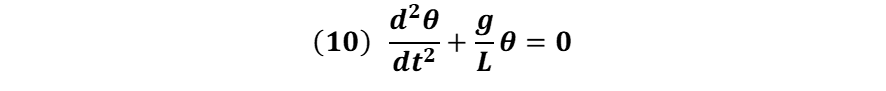
La solución de la ecuación diferencial (10) está dada por:
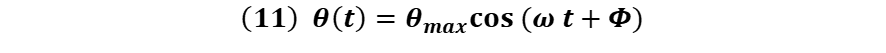
Donde el término “ω" representa la frecuencia angular y esta dada por:
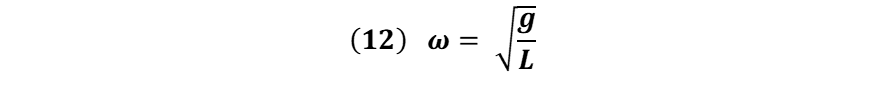
Dado que el periodo de oscilación está definido por:

Para el péndulo simple, el periodo queda expresado como:
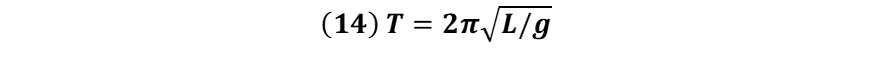
De esta expresión se observa que para un péndulo en movimiento armónico simple el periodo de oscilación depende de su longitud y de la gravedad.
Es esta dependencia la que permite obtener el valor de la gravedad local a partir de diferentes medidas de los valores del periodo de oscilación para determinadas longitudes.
A continuación, se muestra la metodología empleada para determinar el valor de la gravedad local a partir de los valores de oscilación del péndulo versus la longitud.
Si bien estas lecturas pueden obtenerse con la elaboración de un péndulo simple a partir de materiales básicos, en esta oportunidad utilizaremos el simulador phET para obtener dichas lecturas.
En el siguiente video se muestra la obtención de los valores del periodo de oscilación para distintos valores de longitud a través del simulador phET.
A partir de los valores del periodo de oscilación versus la longitud (ver tabla) obtenidos en la simulación, determinaremos la relación lineal entre el cuadrado de dichos periodos y la longitud, tal y como se muestra en la siguiente grafica.

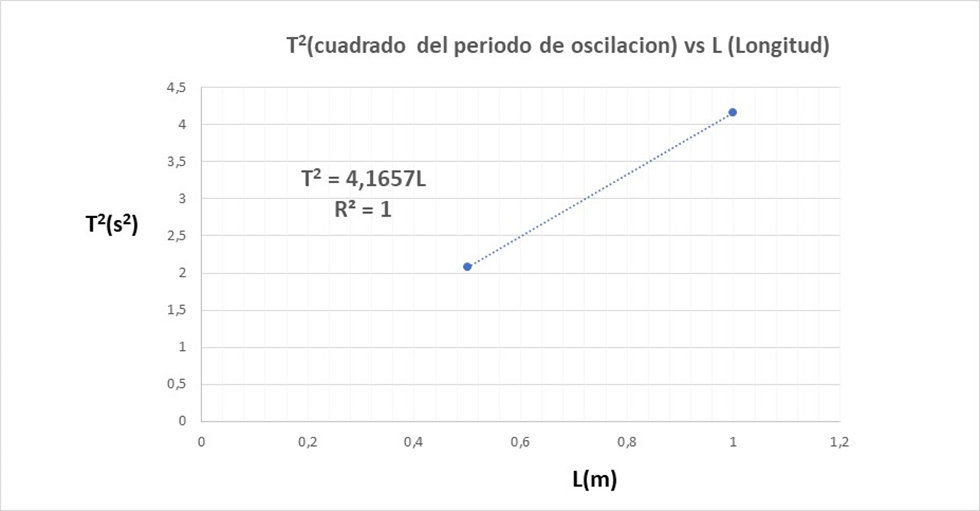
De la ecuación (14) obtenida en nuestro análisis teórico podemos observar que la relación entre el cuadrado del periodo y la longitud es una recta y esta dada por la expresión:
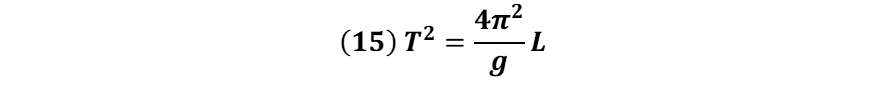
Igualando la ecuación (15) con la expresión de la línea de tendencia obtenida a partir de los valores arrojados por el simulador phET tenemos:

El resultado obtenido nos muestra que la metodología empleada permite obtener el valor de la gravedad, a partir de las variaciones del periodo de oscilación de un péndulo simple debido a las variaciones en su longitud, convirtiendo de esta forma al péndulo simple en un instrumento de medición de un parámetro de importancia en distintas áreas de la ciencia.
Gracias por leer mi publicación, espero que el análisis realizado en este trabajo permita fortalecer y consolidar sus conocimientos en el estudio del movimiento oscilatorio de un péndulo simple y su aplicación en la obtención del valor de la gravedad.
Si tienes alguna duda, pregunta o sugerencia deja tus comentarios y con mucho gusto te responderé.
Referencias
- Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
- Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (80% of the curation rewards are returned).
Please consider including @stemsocial as a beneficiary to get a stronger support.
Hello, could you please contact me with a private message? I just want to ask you some questions :)
Congratulations @lorenzor! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 13000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Buen aporte!