¡Hola amigos de Steemit!
Reciban un cordial saludo.
En esta entrega compartiré con ustedes un análisis teórico y experimental de uno de los principios de conservación cuya aplicación ha permitido el análisis y solución de una gran cantidad de sistemas físicos, en los que los principios de conservación de la energía no son validos o suficientes para la obtención de los parámetros físicos que caracterizan dichos sistemas.
Se trata de nada más y nada menos que del “Principio de conservación de la cantidad de movimiento”.
Este principio, tanto en el caso lineal (PCCML) como en el angular (PCCMA), ha demostrado ser una herramienta valiosa en la descripción de una gran variedad de fenómenos mecánicos, electromagnéticos y de naturaleza cuántica, y cuya validez no se ve restringida por sistemas no conservativos.
Dada la importancia de estos principios, realizaré en este trabajo un desarrollo teórico y experimental donde se demostrará la validez y aplicación de dichos principios, con el fin de fortalecer nuestros conocimientos en áreas de vital interés para la descripción de un sistema.
En nuestro desarrollo experimental utilizaremos como sistema un péndulo balístico, como el que se ilustra en la figura 1, donde obtendremos la velocidad del proyectil (esfera de metal) bajo los principios de conservación PCCML y PCCMA, la cual será verificada con equipos de medición de alta precisión.
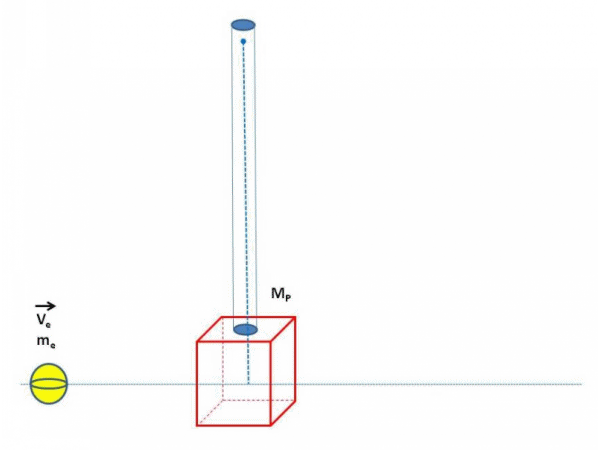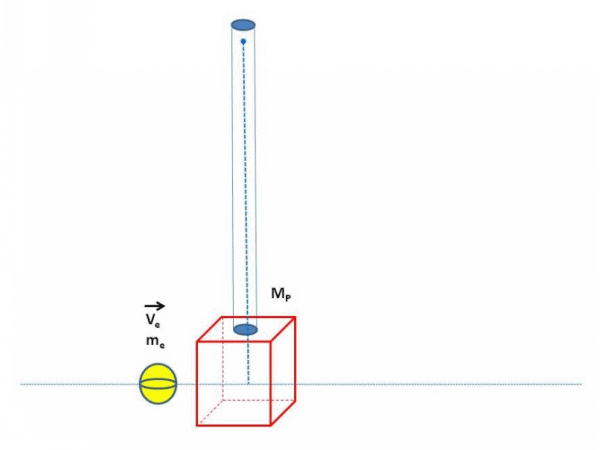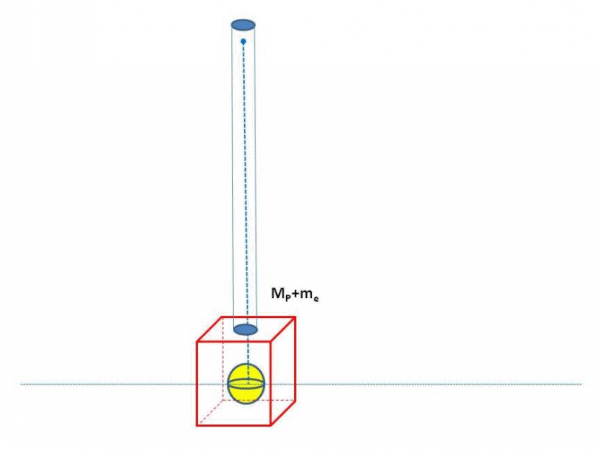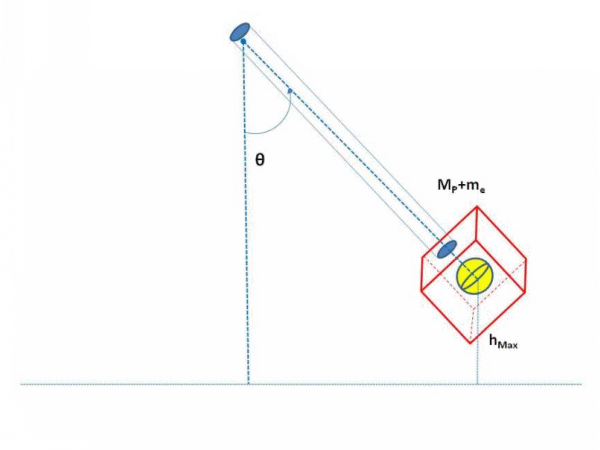 Figura 1 – Representación grafica de la dinámica del péndulo balístico utilizado
Figura 1 – Representación grafica de la dinámica del péndulo balístico utilizado
(Gif elaborado por @lorenzor en PowerPoint y PhotoScape)
Fundamentos teóricos
En muchos casos la segunda ley de Newton es expresada según lo muestra la ecuación (1), para el caso donde la masa se mantiene contante:

Sin embargo, existen una gran variedad de casos donde la masa no preserva su valor, por lo que es necesario escribir en forma general la segunda Ley de Newton según lo expresa la siguiente ecuación:
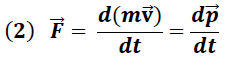
Donde el término " " dado por la expresión (3):
" dado por la expresión (3):

es conocido como la cantidad de movimiento lineal (momento lineal) de un objeto.
m → masa del objeto
 → Velocidad del objeto
→ Velocidad del objeto
Para un sistema constituido por “n” partículas la expresión (3) se generaliza de la forma:
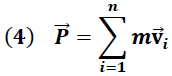
Para un sistema sometido a un conjunto de fuerzas, la ecuación (2) es escrita como:

Donde

representa La fuerza total externa que actúa sobre el sistema y

es el momento lineal total.
En la expresión (5) se observa que:
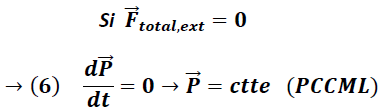
La expresión (6) nos indica que el momento lineal del sistema permanece invariante siempre que la contribución de todas las fuerzas externas que actúan sobre el sea nula.
Para sistemas en rotación es necesaria la inclusión del concepto de momento de Fuerza (torque) definido por la expresión (7), el cual es utilizado en los casos donde la aplicación de una fuerza
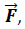
o un conjunto de ellas, da origen a una rotación, lo que hace necesario la incorporación de una cantidad de movimiento de tipo angular.
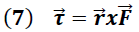
De forma análoga a la ecuación (5), en el caso rotacional se tiene una expresión que asocia el cambio temporal de la cantidad de movimiento angular
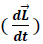
con el momento de fuerza total
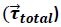
que actúa sobre el sistema, dado por la siguiente expresión:
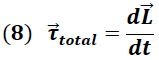
Donde

representa la cantidad de movimiento angular (momento angular) y esta dado por el producto vectorial que se muestra a continuación:
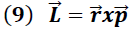
En magnitud la expresión (9) toma la forma:
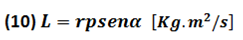
α → ángulo entre p y r
r → distancia entre el eje de rotación y centro de masa del objeto
En la ecuación (8) se observa que:
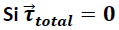
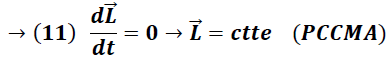
Bajo la condición planteada se tiene que la cantidad de movimiento angular permanece invariante.
Parte experimental
Materiales y equipos utilizados
 Figura 2 – Materiales y equipos utilizados
Figura 2 – Materiales y equipos utilizados
(Fotografía tomada en el laboratorio por @lorenzor)
Metodología
En las siguientes imágenes se muestra el montaje del equipo utilizado y el análisis de la dinámica del movimiento lineal y rotacional del sistema.
 Figura 3 – Montaje real del péndulo balístico utilizado en el laboratorio
Figura 3 – Montaje real del péndulo balístico utilizado en el laboratorio
(Fotografía tomada en el laboratorio por @lorenzor y editada en PowerPoint)
 Figura 4 – Análisis dinámico y geométrico del péndulo balístico después del impacto
Figura 4 – Análisis dinámico y geométrico del péndulo balístico después del impacto
(Elaborado por @lorenzor en PowerPoint)
La metodología utilizada, según se aprecia en la figura 3, consiste en disparar una esfera metálica con el lanzador (projectile launcer), la cual impactara con el péndulo (choque inelástico), desplazándolo hasta un punto máximo registrado por el equipo.
Nuestro objetivo consistirá, con la data obtenida, en determinar la velocidad del proyectil (esfera metálica) a partir de los principios de conservación PCCML y PCCMA, la cual será verificada experimentalmente con el uso de sensores de alta precisión.
Método 1: (PCCML)
En nuestro primer análisis obtendremos la velocidad de la esfera de metal usando el principio de conservación (PCCML), considerando que la masa del sistema (esfera de metal-bloque de captura) está ubicada en el centro de masa (CM) de dicho sistema.
La Cantidad de movimiento de la esfera antes del impacto:
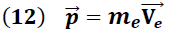
me → masa de la esfera de metal
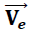 → Velocidad de la esfera
→ Velocidad de la esfera
En magnitud:
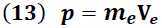
En el impacto, el nuevo sistema que forma la esfera de metal y el bloque de captura adquieren una energía cinética
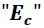
la cual está definida a partir de la siguiente expresión:
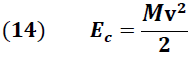
Donde:
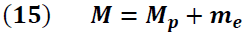
Mp → masa del péndulo
La expresión (14) puede reescribirse de la forma:
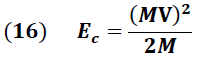
En la ecuación (16) se observa que el término "MV" representa la cantidad de movimiento "p" que adquiere el sistema esfera-bloque de captura.
Esto nos permite obtener el valor de "p" luego del impacto como una función de la energía cinética adquirida, según se muestra a continuación:
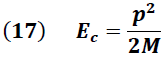
Despejando "p" se obtine:

Aplicando el principio de conservación PCCML:
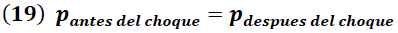
Se obtiene:
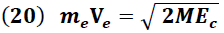
Según la conservación de la energía, en el punto de impacto, la energía cuya naturaleza es totalmente cinética se transforma a potencial en el punto máximo alcanzado por el péndulo.
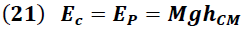
g → aceleración de la gravedad = 9,8 m/s2
hCM → Altura máxima del centro de masa (m)
De la geometría visualizada en la figura 4 se tiene que:
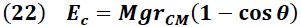
Sustituyendo (22) en (20):
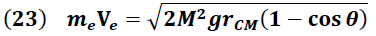
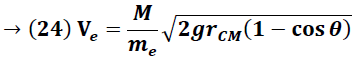
Valores obtenidos en el laboratorio
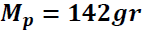
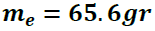
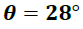
En la siguiente imagen se muestra la posición del centro de masa del péndulo. Para este fin se utilizo una cuerda de suspensión que fue desplazada hasta ubicar el punto de equilibrio.
 Figura 5 – Ubicación experimental del centro de masa del péndulo
Figura 5 – Ubicación experimental del centro de masa del péndulo
(Fotografía tomada en el laboratorio por @lorenzor)
Cálculos y resultados
De la ecuación (24) se obtiene que la velocidad de la esfera de metal está dada por el siguiente valor:
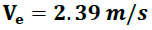
Metodo2: (PCCMA)
La velocidad de la esfera de metal puede obtenerse de manera más precisa a partir del principio de conservación PCMA incorporando en el análisis la inercia rotacional del sistema.
Antes del impacto, la cantidad de movimiento angular de la esfera de metal esta dado por la expresión:
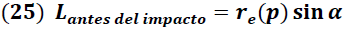
re → distancia entre el eje de rotación y centro de masa de la esfera
α → angulo entre p y re = 90°
p → me Ve
Después del impacto, el momento angular puede asociarse de forma similar que en el método anterior con la energía cinética rotacional a partir de la siguiente expresión:

I → Momento de Inercia [Kg.m2 ]
Despejando "L" de (26) se obtiene:
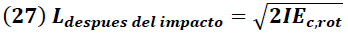
Según el principio de conservación de PCCMA:

Se obtiene:
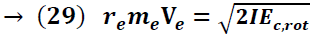
Donde:
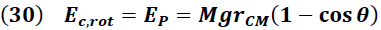
Sustituyendo (30) en (29) obtenemos:
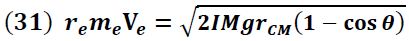
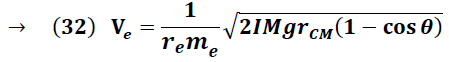
El momento de inercia del péndulo físico (compuesto) es obtenido a partir del análisis de su dinámica rotacional, del que se obtiene la siguiente expresión:

Sustituyendo (33) en (32) obtenemos:

El periodo de oscilación es obtenido haciendo oscilar el péndulo desde su máximo desplazamiento angular, según se muestra en la siguiente imagen:
 Figura 6 – Determinación experimental del periodo de oscilación del péndulo
Figura 6 – Determinación experimental del periodo de oscilación del péndulo
(Fotografía tomada en el laboratorio por @lorenzor)
Valores obtenidos en las mediciones

Cálculos y resultados obtenidos
De la ecuación (34) se obtiene que la velocidad de la esfera de metal según el principio de conservación PCCMA, tiene un valor de:

Método de verificación experimental de la velocidad de la esfera de metal
Los valores de velocidad obtenidos por el método 1 (PCCML) y el método 2 (PCCMA) son verificados experimentalmente por el método de las dos fotosceldas utilizado en mi artículo
movimiento parabólico.
En el experimento 2 de ese artículo se obtuvo la velocidad de salida de la esfera plástica (amarilla) utilizando dos fotoceldas conectadas al smart-time (medidor de tiempo), el cual arroja el valor del tiempo de transito de la esfera entre dichas fotoceldas separadas 10 cm.
En esta oportunidad siguiendo el mismo procedimiento (ver figura 7), se obtiene la velocidad de salida de la esfera de metal utilizada en este trabajo.
 Figura 7 – Determinación experimental de la velocidad de la esfera de metal antes del impacto
Figura 7 – Determinación experimental de la velocidad de la esfera de metal antes del impacto
(Fotografía tomada en el laboratorio por @lorenzor)
Valores obtenidos en las mediciones
 (Separación entre los dos sensores)
(Separación entre los dos sensores)
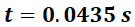 (tiempo de transito entre los sensores)
(tiempo de transito entre los sensores)
Velocidad de la esfera de metal
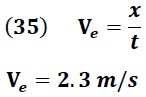
Error porcentual del Método 1 (PCCML) respecto al equipo de medición:
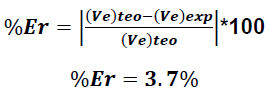
Error porcentual del Método 2 (PCCMA) respecto al equipo de medición:
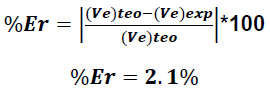
De los resultados obtenidos podemos apreciar que las velocidades calculadas bajo los principios de conservación PCCML y PCCMA coinciden con una alta precisión con el arrojado por el instrumento de medición, validando de esta forma los principios de conservación a los cuales responde la cantidad de movimiento lineal o angular de un sistema.
La validez y aplicación de estos principios de conservación han contribuido con la solución de una gran variedad de sistemas y han sido el punto de partida en el estudio de colisiones de objetos y partículas, los cuales han conducido a resultados y formulaciones cuya obtención no habría sido posible sin el uso de estas leyes de conservación.
Espero que el análisis teórico y experimental desarrollado en este trabajo permita fortalecer tus conocimientos sobre las leyes de conservación inherentes a la cantidad de movimiento lineal y angular de un cuerpo. Si tienes alguna duda, pregunta o sugerencia, deja tus comentario y con mucho gusto te responderé.
Gracias por leer mi publicación.
Referencias
- Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
- Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.


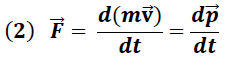
 " dado por la expresión (3):
" dado por la expresión (3):
 → Velocidad del objeto
→ Velocidad del objeto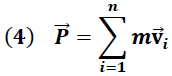

 representa La fuerza total externa que actúa sobre el sistema y
representa La fuerza total externa que actúa sobre el sistema y  es el momento lineal total.
es el momento lineal total.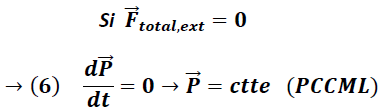
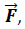 o un conjunto de ellas, da origen a una rotación, lo que hace necesario la incorporación de una cantidad de movimiento de tipo angular.
o un conjunto de ellas, da origen a una rotación, lo que hace necesario la incorporación de una cantidad de movimiento de tipo angular. 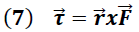
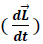 con el momento de fuerza total
con el momento de fuerza total 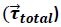 que actúa sobre el sistema, dado por la siguiente expresión:
que actúa sobre el sistema, dado por la siguiente expresión: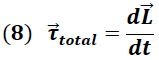
 representa la cantidad de movimiento angular (momento angular) y esta dado por el producto vectorial que se muestra a continuación:
representa la cantidad de movimiento angular (momento angular) y esta dado por el producto vectorial que se muestra a continuación: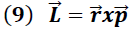
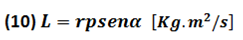
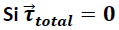
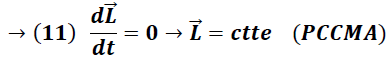



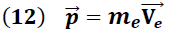
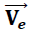 → Velocidad de la esfera
→ Velocidad de la esfera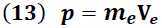
 la cual está definida a partir de la siguiente expresión:
la cual está definida a partir de la siguiente expresión: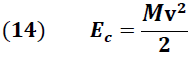
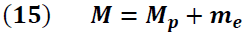
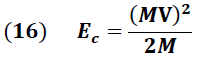
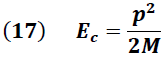

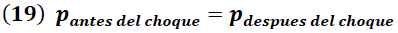
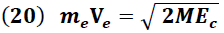
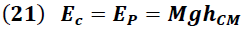
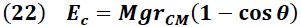
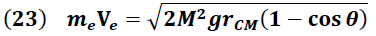
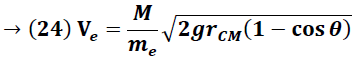
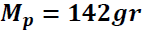
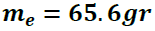
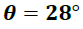

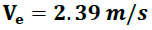
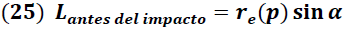

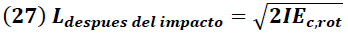

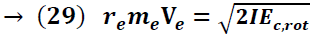
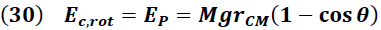
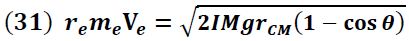
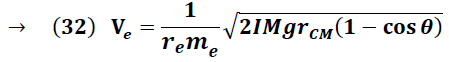






 (Separación entre los dos sensores)
(Separación entre los dos sensores)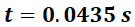 (tiempo de transito entre los sensores)
(tiempo de transito entre los sensores)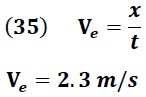
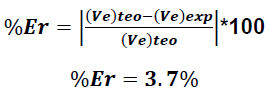
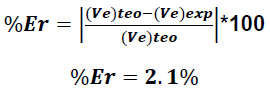
Estas participando para optar a la mención especial, que se efectuará el 05 de Agosto del 2018 a las 8:00 pm (hora de Venezuela); donde el autor del artículo seleccionado recibirá la cantidad de 1 SBD transferidos a su cuenta.
Contáctanos en Discord: https://discord.gg/hkCjFeb
Apoya al trail de entropía y así podrás ganar recompensas de curación de forma automática, entra aquí para más información sobre nuestro TRAIL.
Puedes consultar el reporte diario de curación visitando @entropia
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Excelente forma de enseñar los principios físicos teóricos con experimentos ya que así podemos ver en primera fila como se cumplen estos principios.
Muy buen artículo Profe, estaré revisando los anteriores y pendientes de los futuros, son un valioso aporte.
Saludos @zambranoacosta. gracias por tu apoyo. Me alegra te gustara el trabajo.
Tremendo trabajo mi amigo y colega @lorenzor. Excelente contenido y presentación. Veo que ya estás incursionando en el campo de los gifs animados.
¡Mis felicitaciones!
Un abrazo.
saludos mi estimado amigo y colega @tsoldovieri. Su visita y comentario positivo siempre es de gran apoyo. Gracias por comentar.
Hi @lorenzor!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Gracias por el apoyo.
Hola, @lorenzor, quiero felicitarte por tu trabajo en esta plataforma, pero aún más por la calidad y didáctica que le imprimes. Tu manera que enseñar la Física tiene un valor agregado de mucha relevancia por cuanto te vales de lo experimental para que quienes te seguimos podamos corroborar lo que la teoría predice. comentado, votado y reesteemeado.
Gracias amigo @reyito. Su apoyo y comentario son motivadores.
Hola Lorenzo. Leyendo tu trabajo me preguntaba sobre la posibilidad de realizar esas medidas en un péndulo esférico... Te dejo esa inquietud...
Un abrazo...
Saludos mi estimado amigo @jfermin70. Siempre un honor tenerlo de visita por aquí. Su propuesta me parece interesante. si bien el tratamiento teórico es mucho mas complejo un ensayo experimental seria de gran apoyo. Tendría que pensar en un diseño experimental que me permita obtener las medidas necesarias. Tomare su idea. Gracias por el apoyo. Saludos
Felicitaciones estimado @lorenzor por este post. La experiencia práctica atrae y motiva. Estoy seguro que entendidos y aprendices lo aprovecharán. Saludos !
Saludos estimado @tomastonyperez. Gracias por tu comentario. Tu palabras me motivan. Saludos amigo.
Excelente post profesor, todo muy bien explicado y demostrado. Siempre me emociona cada vez que los resultados teóricos y experimentales coinciden de esa manera. Procuraré llegar en algún momento a ese nivel de dominio de la materia. Saludos !
Gracias @marcosdm. Me alegro que te guste el trabajo y el contenido que comparto .Espero te sea útil. Gracias por el apoyo y el comentario. Seguro tus trabajos serán de mucha utilidad y calidad.
Me gusto mucho como explicas la metodología por medio de las fotografías y la edición que realizas, el experimento esta muy bien estructurado. Aprendiendo un poco más de esta área tan fascinante..Saludos profesor
Saludos anaestrada12. Gracias por tu comentario y apoyo.Me alegra te gustara el trabajo. Espero tener el honor de tener tu visita en trabajos futuros .Gracias
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Mi agradecimiento por el apoyo recibido.
Hola @lorenzor, Es bastante completo tu trabajo, tanto en lo teórico como lo experimental. Seria interesante estudiar el péndulo cónico en forma teórica y experimental. Es posible que se haga una simulación de ese movimiento cónico, faltaría la experimentación. Te felicito buen trabajo.
Saludos @germanmontero. Gracias por la lectura y el comentario. Seria interesante ese desarrollo experimental. De seguro revisare la posibilidad de un diseño experimental que permita obtener las medidas requeridas. Gracias por su idea y apoyo.
Saludos estimado @lorenzor. Excelente el trabajo, muy bien desarrollado y didáctico, siempre me ha gustado ver la demostración de todos estos fenómenos, corroborarlos siempre es un gran método de enseñanza.
Saludos estimado @emiliomoron. Me alegra que le guste el trabajo teórico y experimental que presento. Ciertamente la demostración experimental nos permite ver con mas claridad los fenómenos físicos. Gracias por su apoyo.
Saludo profesor lorenzo excelente explicacion de este experimento. lo sigo sigo
@alberth
Saludos @alberth. Gracias por el apoyo y la visita. Espero llamar tu atención en mis artículos futuros.