INTRODUCCIÓN
En la entrega anterior (ver ref. 04), dimos inicio al abordaje matemático-conceptual del fenómeno de consolidación unidimensional de los suelos, donde destacan como principales ideas, el hecho de considerarlos en una condición saturada y de concebir los asentamientos verticales que ocurren diferidos al tiempo de aplicación de las cargas, como una consecuencia de disipación de la presión en exceso a la hidrostática “u”; lo cual se materializa en agua que es expulsada del suelo en cuestión, con una dirección de flujo en sentido vertical, hecho que provoca en la misma proporción que ocurre, el incremento de los esfuerzos efectivos “σ’” y por consiguiente los asentamientos anteriormente descritos. El fenómeno de consolidación unidimensional de los suelos, está por lo tanto íntimamente vinculado a la variación del exceso de la presión a la hidrostática “u”; una variación que está influenciada por el tiempo que ha pasado posterior a la aplicación de las cargas, y por la profundidad “z” del estrato que se esté analizando.
Imagen N°01: una visión global de los contenidos a abordar
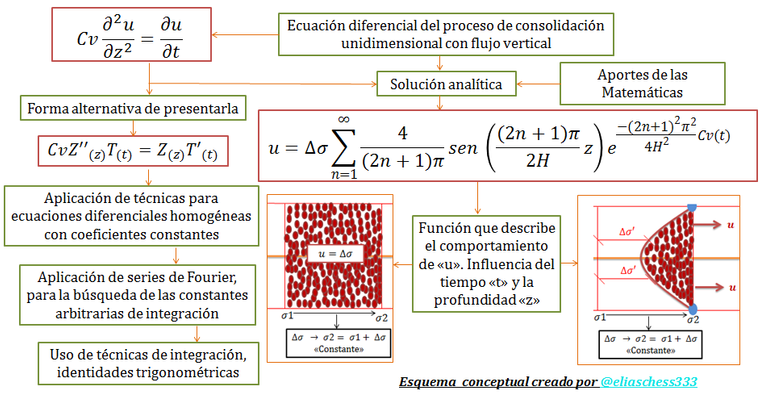
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Lo anteriormente expuesto, constituye las principales hipótesis de partida, que permitieron a Terzaghi el desarrollo de la “Ecuación Diferencial del Proceso de Consolidación Unidimensional con Flujo Vertical”:
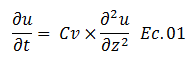
Esta ecuación es presentada de una forma alternativa, tal como se aprecia en el esquema conceptual de la imagen N°01, y es el punto de partida para deleitarnos con los aportes de las matemáticas enmarcados en la aplicación de técnicas de resolución de ecuaciones diferenciales homogéneas con coeficientes constantes y así posteriormente aplicar las series de Fourier para determinar los valores de las constantes de integración involucradas; todos estos procedimientos los estaremos desarrollando con la finalidad de encontrar la solución analítica de la ecuación N°01, y así seguir profundizando en este interesante fenómeno de importancia en la ingeniería geotécnica, como lo es la consolidación unidimensional de los suelos.
UNA VISIÓN DIDÁCTICA DEL ESTABLECIMIENTO DE LAS CONDICIONES DE BORDE
Dado que deseamos resolver de forma analítica la ecuación N°01, es necesario establecer unas condiciones de borde, lo cual orientará los procesos de cálculo diferencial que desarrollaremos en líneas posteriores. Para tal fin, tomemos como referencia el esquema conceptual de la imagen N°02:
Imagen N°02: ilustración didáctica de la condición frontera “u=0” para “z=0 y z=2H”
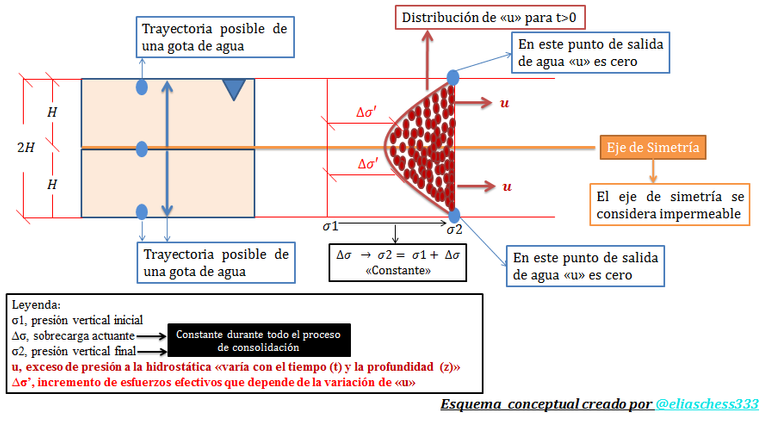
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Esta primera condición de borde, establece que tiempo después de aplicada la carga “∆σ”, el exceso de presión a la hidrostática “u” en la parte superior e inferior de un estrato que se supone drenado por ambas caras, es cero; hecho que se puede interpretar fácilmente, asociándolo con una salida de agua, la cual ocurre gradualmente por la baja permeabilidad de los suelos que experimentan este fenómeno, como por ejemplo, las arcillas. En el eje de simetría, resaltado por el color “naranja”, se supone que “u” alcanza sus valores máximos, dado que el mismo se considera impermeable, lo cual es un criterio aceptable, ya que el agua tiene dos posibles trayectorias de salida, debido a que el estrato está drenado por ambas caras. La otra condición frontera de importancia se ilustra en el esquema conceptual de la imagen N°03:
Imagen N°03: ilustración didáctica de la condición frontera “u=∆σ” para “t=0 y 0<z<2H”
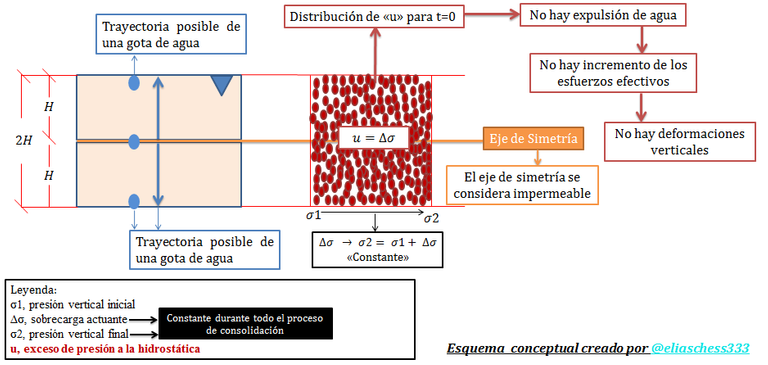
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Para comprender esta condición, tomemos como referencia la analogía mecánica de Terzaghi, sobre la que puedes profundizar en la referencia N°04 donde realicé un video explicativo al respecto. Se tiene entonces que al aplicar las cargas “∆σ”, en un instante de tiempo teóricamente igual a “cero”, el agua que satura el estrato de suelo se presuriza, es decir, surge una presión en exceso a la hidrostática “u”, que se distribuye uniformemente en el mismo. Esto tiende a ocurrir en suelos de naturaleza arcillosa producto de su baja permeabilidad, siendo muy difícil una expulsión inmediata de agua, hecho que constituye, el sustento de la hipótesis anteriormente planteada. Una vez comprendida la lógica de las condiciones de borde, adentrémonos en la solución analítica de la ecuación N°01.
APLICACIÓN DE LA TÉCNICA DE RESOLUCIÓN DE ECUACIONES DIFERENCIALES HOMOGÉNEAS CON COEFICIENTES CONSTANTES
Lo anteriormente expuesto, permite establecer que “u” depende de la profundidad “z” y del tiempo “t”, lo cual podemos representar de la siguiente forma:
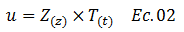
Esta ecuación sirve de base para reescribir la ecuación N°01, procedimiento que se ilustra en el esquema conceptual de la imagen N°04:
Imagen N°04: rescribiendo la ecuación diferencial de consolidación unidimensional
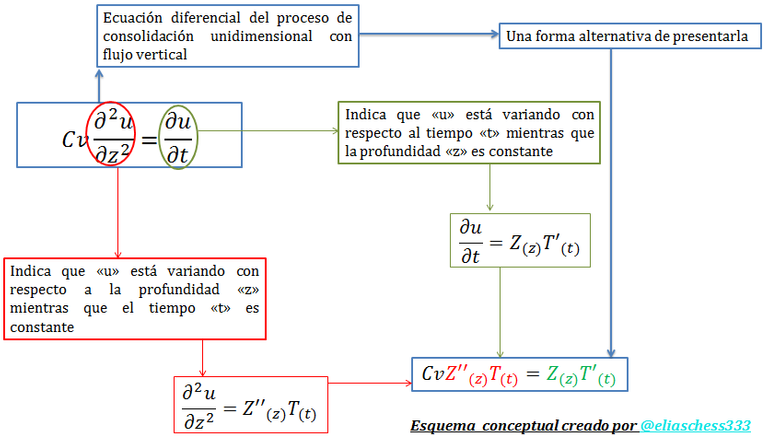
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Basados en la forma alternativa de presentar la ecuación N°01, la misma puede ser rescrita de la siguiente manera:
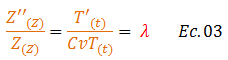
El término resaltado en color “rojo” en la ecuación N°03, es una constante que se puede introducir, fundamentándonos en la igualdad que existe entre los cocientes resaltados por el color “naranja”. Esto contribuye al surgimiento de las siguientes ecuaciones:
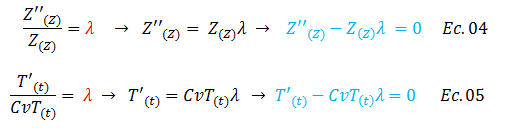
Las ecuaciones resaltadas en color “azul”, son ecuaciones diferenciales homogéneas con coeficientes constantes, por lo que procedemos a aplicar las técnicas de resolución de ecuaciones diferenciales ajustadas a dicho caso.
• ABORDAJE MATEMÁTICO ECUACIÓN N°04
Para tal fin nos valemos de las bondades de la función exponencial “e^x”, representadas por el hecho de que sus derivadas son múltiplos de la misma función. Por lo que para la ecuación N°04 se puede plantear como posible solución:
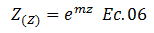
Obtenemos la primera y segunda derivada con respecto a “z” de la ecuación N°06:
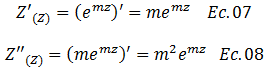
Al sustituir las ecuaciones N°06 y N°08 en la N°04 obtenemos lo siguiente:
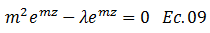
Sacamos factor común:
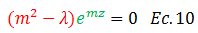
Dado que el término resaltado en color “verde” de la ecuación N°10 no se anula, para que esta se cumpla, la función auxiliar resaltada en color “rojo” debe ser cero, por lo que:
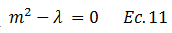
Aplicamos la técnica de resolvente, para encontrar los posibles valores de “m”, donde:
a=1
b=0
c=-λ
Entonces:
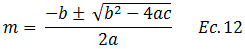
Sustituyendo en la ecuación N°12 tenemos:
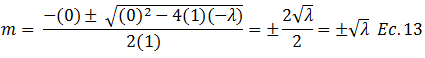
Por lo que las posibles soluciones de la ecuación N°04 vienen dadas por:
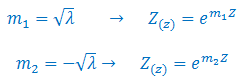
Siendo la solución general la suma de ambas, y en cuyo planteamiento se introducen las constantes arbitrarias de integración:
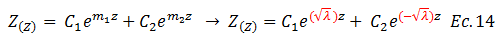
Basados en las condiciones fronteras presentadas en el esquema conceptual de la imagen N°02, y aplicadas a la ecuación N°02, se tiene:
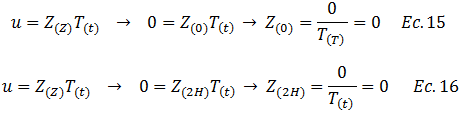
Estos resultados permiten abordar la ecuación N°14 con la finalidad de esclarecer el camino en la búsqueda de las constantes de integración “c1” y “c2”, por lo que al evaluar dicha ecuación para “z=0” se tiene:
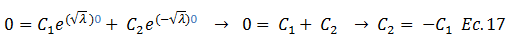
Esto permite rescribir la ecuación en cuestión de la siguiente manera:
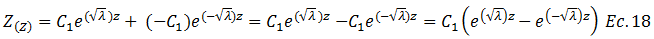
La ecuación N°18 nos permite introducir la identidad trigonométrica asociada al seno hiperbólico:
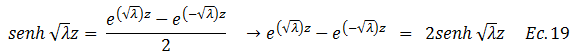
Al sustituir la ecuación N°19 en la N°18, obtenemos:
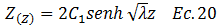
Basado en la condición de borde desarrollada en la ecuación N°16, sustituimos en la ecuación N°20 (ver términos resaltados en color “azul”):
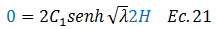
Estratégicamente procedemos a rescribir la ecuación N°21 de la siguiente manera:
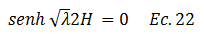
Dado que el seno hiperbólico de un argumento imaginario es el seno trigonométrico con el mismo argumento, se puede plantear como valor de “λ” el siguiente:
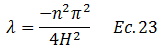
Sustituimos este valor en la solución en la ecuación N°22:
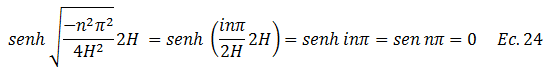
A partir de estas deducciones podemos reescribir la ecuación N°20, teniendo la precaución de colocar en el argumento de la función seno, una relación de proporcionalidad entre la profundidad de interés “z” y el espesor del estrato “2H”; esta relación se encuentra resaltada por el color “rojo”:
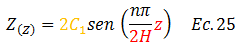
Esta ecuación constituye una forma general de presentar la ecuación N°21. A pesar de que el término resaltado en color “naranja” aparece multiplicado por “2”, puede considerarse como la existencia de una única constante arbitraria, por lo que para hacer más cómodo el manejo de esta ecuación, al momento de sustituir en la ecuación N°02, se tiene que:
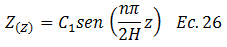
• ABORDAJE MATEMÁTICO ECUACIÓN N°05
De igual forma como se trató la ecuación N°04, planteamos como posible solución la siguiente:
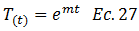
Obtenemos la primera derivada con respecto al tiempo “t”:
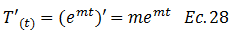
Sustituimos las ecuaciones N°27 y N°28 en la ecuación N°05:
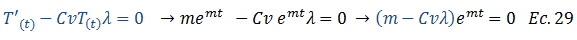
Dado que el término exponencial no se cancela, la ecuación N°29 se satisface para cuando la función auxiliar resaltada por el color “azul” es igual a cero, por lo tanto:
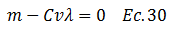
Por lo que:
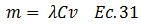
Introduciendo la constante arbitraria de integración y tomando como referencia el valor para “λ” planteado en el tópico anterior, la solución de la ecuación N°05 viene dada por:
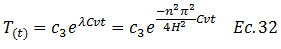
• UNA VISIÓN DE LOS AVANCES LOGRADOS EN LA BÚSQUEDA DE LA SOLUCIÓN ANALÍTICA DE LA ECUACIÓN N°01
Dado que el proceso de consolidación está gobernado por las variaciones de “u” en el tiempo “t” y profundidad “z”, se procedió al desarrollo de la ecuación N°02, y de las que se presentan en el esquema conceptual de la imagen N°04. El abordaje matemático de tales ecuaciones, ha permitido obtener lo siguiente:
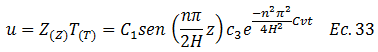
Rescribimos:
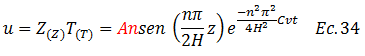
El término “An” representa las constantes arbitrarias de integración, que depende de los valores de “n”. Como se puede apreciar, el reto que a continuación sigue es encontrar el valor de “An”. Para tal fin, haremos uso de otro de los grandes aportes de las matemáticas como lo son las series de Fourier, lo cual se desarrolla a continuación:
SERIES DE FOURIER ¡AL RESCATE!
Las Matemáticas nos sorprenden con la infinidad de aplicaciones que contribuyen a una mejor comprensión de los fenómenos físicos que ocurren a nuestro alrededor, centrándonos en este caso en el fenómeno de consolidación unidimensional de los suelos. Haremos uso de las series de Fourier para finalmente dar con la solución analítica de la ecuación N°01. Para una mejor comprensión de este tópico, lo he subdivido en las siguientes partes:
• UN ENFOQUE TEÓRICO-CONCEPTUAL DE LAS SERIES DE FOURIER
La presencia de derivadas parciales en la ecuación N°01 producto de que la presión en exceso a la hidrostática “u”, depende de dos variables como lo son el tiempo “t” y la profundidad “z”, y la necesidad de encontrar el valor de “An” para dar finalmente con la solución general de dicha ecuación, son situaciones que abren las puertas al uso de las series de Fourier.
En primer lugar presentemos la forma general de una serie de Fourier:
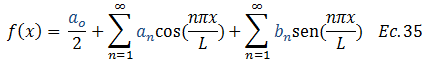
Se establecen como principales hipótesis en torno a la ecuación N°35, que la suma de sus términos converge al valor de la función, y que toda la función es integrable en el rango de valores que va de “-L” a “L”, siendo el cero “0” el punto medio del intervalo y matemáticamente se expresa así:
El reto es encontrar los valores de los coeficientes resaltados en color “azul” en la ecuación N°35. Para encontrar por ejemplo el coeficiente “ao” se procede a la integración de cada uno de los términos de dicha ecuación, lo cual se ilustra didácticamente en el siguiente esquema conceptual:
Imagen N°05: determinación analítica del coeficiente “ao”
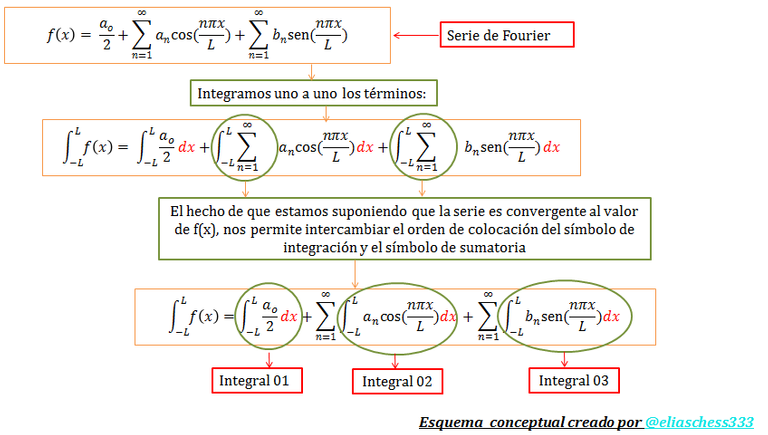
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Procedemos a resolver cada una de las integrales señaladas en la imagen N°05. Vale destacar que en el proceso de obtención de la integral definida, el término resaltado en color “verde” representa los límites de evaluación de la integral. En lo que respecta a la “integral 1” se tiene:
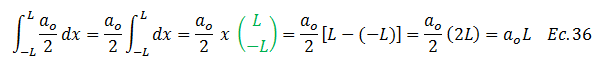
Para el caso de la “integral 2”:
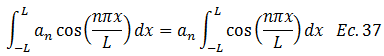
Aplicamos la técnica de integral por sustitución, donde:
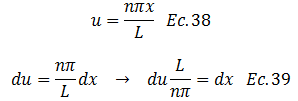
Sustituimos las ecuaciones N°38 y N°39 en la N°37:
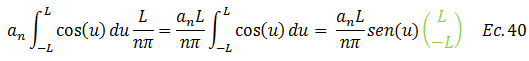
Devolvemos el cambio, sustituyendo la ecuación N°38 en la N°40:
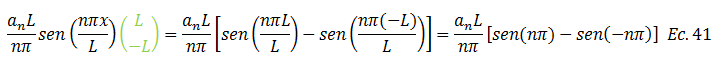
Al ser el seno de cualquier múltiplo de “π” igual a cero, se tiene que:
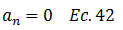
Algo similar ocurre en la solución de la “integral 3”:
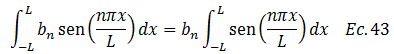
Dado que la función a integrar tiene el mismo argumento que el de la “integral 2”, podemos usar las ecuaciones N°38 y N°39 en el proceso de integración por sustitución:
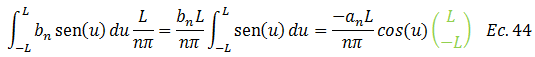
Devolvemos el cambio sustituyendo la ecuación N°38 en la N°44:
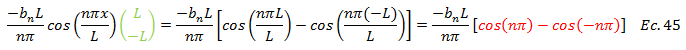
Por ser el coseno una función par:
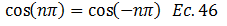
El término resaltado en color “rojo” de la ecuación N°45 se cancela, obteniendo que:
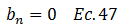
Dado que el resultado de “integrales 2 y 3” es cero, estas se omiten al realizar la suma de los resultados del proceso de integración definida en pro de conseguir el coeficiente “ao”, en este orden de ideas:
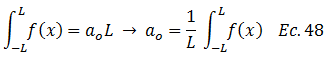
Contextualicemos todos estos conocimientos al caso en estudio.
• APLICACIÓN DE LAS SERIES DE FOURIER AL CASO EN ESTUDIO
Basados en la condición de borde del esquema conceptual de la imagen N°03:
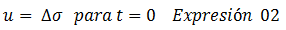
Evaluamos la ecuación N°34 para este tiempo:
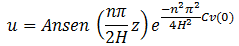
Por lo tanto:
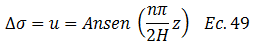
Dado que “∆σ” es constante en todo el proceso de consolidación, “u” también lo es para el instante de tiempo teóricamente considerado como cero “0”, por lo que es necesario concebir “u” como una suma infinita de términos sinusoidales, dando así la bienvenida a la serie de Fourier:
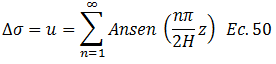
Al contrastar la ecuación N°50 con la N°35 (forma general de la serie de Fourier), el problema en estudio sólo tiene el término relativo a la función seno, por lo se reduce a encontrar el coeficiente “bn” (Ec.35), que es el mismo “An” (Ec.50). En el tópico anterior demostramos que al aplicar la técnica de integral definida a cada miembro de la ecuación no nos ayuda a encontrar este coeficiente. Para tal fin, lo que se recomienda es multiplicar ambos lados de la ecuación N°50 por el término:
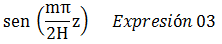
Obteniendo lo siguiente:
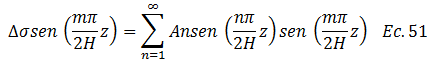
Y de este modo proceder a integrar a ambos lados, acotando que los límites de integración, están definidos por el espesor del estrato “ver imágenes N°02 y N°03”
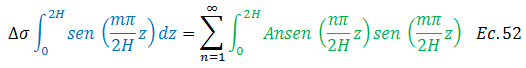
Procedemos a resolver las integrales resaltadas por los colores “azul” y “verde”:
• RESOLVIENDO LA INTEGRAL RESALTADA EN COLOR “AZUL”
En el esquema conceptual de la imagen N°06 se ilustra este procedimiento:
Imagen N°06: solución integral resaltada con el color "azul" (Ec.52)
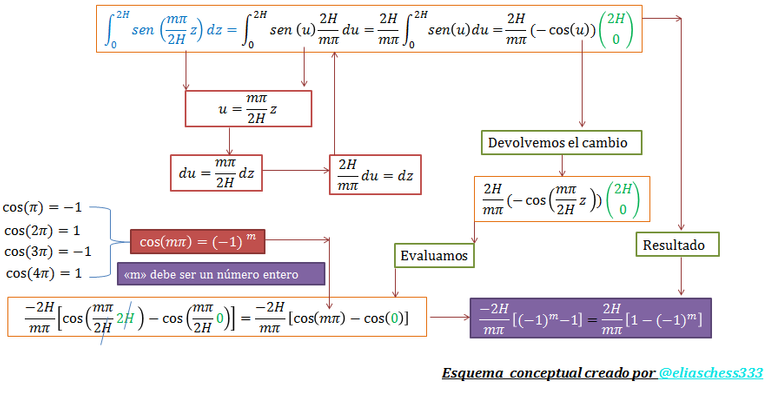
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
• RESOLVIENDO LA INTEGRAL RESALTADA EN COLOR “VERDE” PARA “n≠m”
En primera instancia es necesario rescribir la integral, lo cual se plasma en la siguiente imagen:
Imagen N°07: rescribiendo la integral resaltada en color "verde" (Ec.52), caso “n≠m”
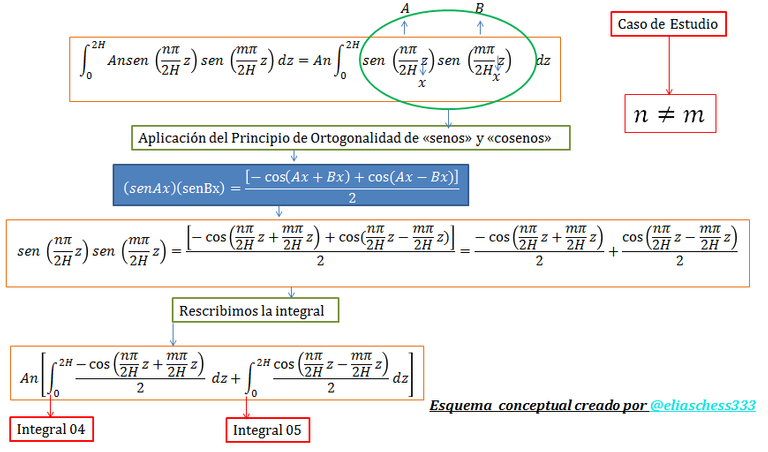
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Procedemos a resolver la “integral 04”, de la siguiente manera:
Imagen N°08: resolución de la “integral 04”
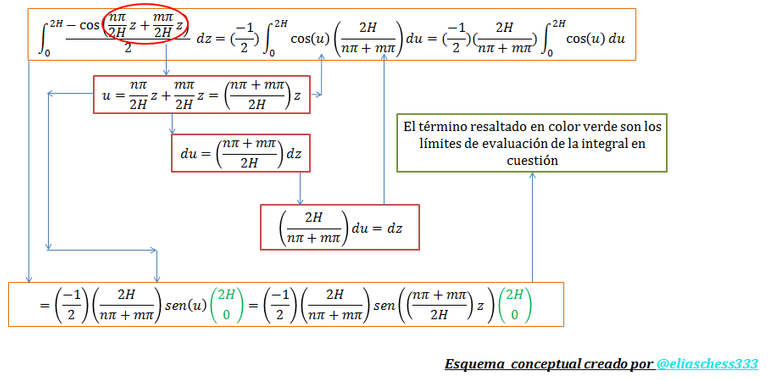
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
La evaluación de la “integral 04” en los límites resaltados por el color “verde” y que representan el espesor del estrato de suelo, se ilustra a continuación:
Imagen N°09: evaluación de la integral 04
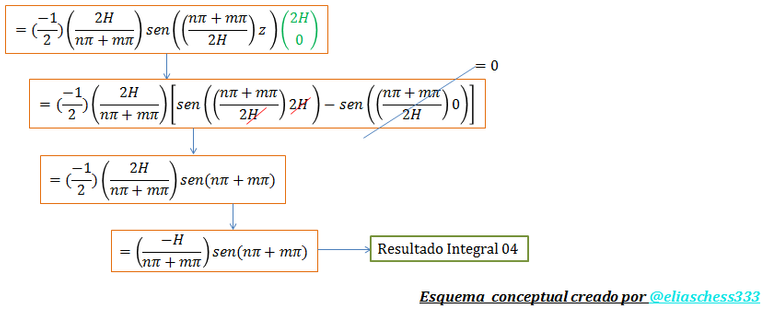
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
En lo que respecta a la “integral 05” tenemos lo siguiente:
Imagen N°10: resolución de la integral 05
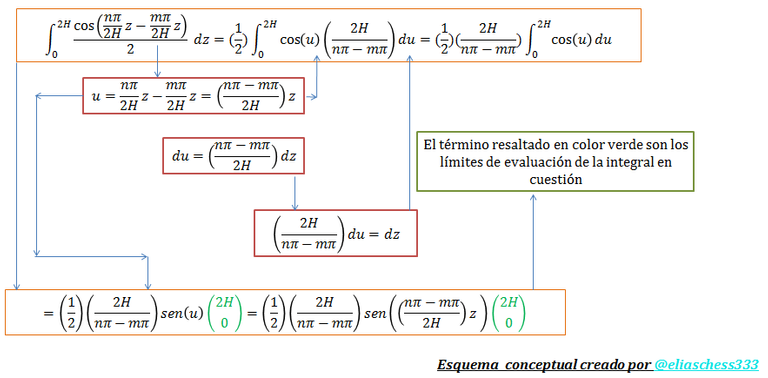
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Evaluamos el resultado en los respectivos límites de integración:
Imagen N°11: evaluación de la “integral 05”
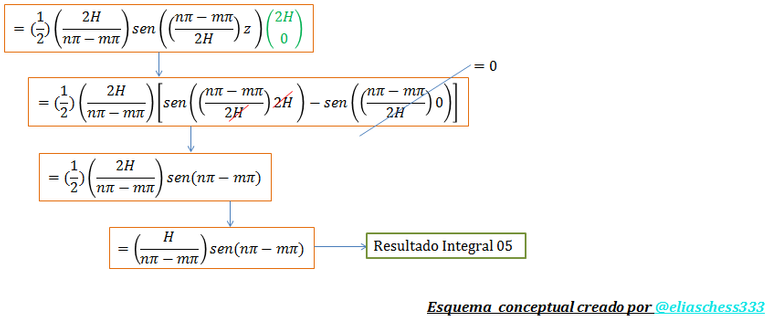
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Estos resultados parciales se suman, para dar con el resultado de la integral resaltada por el color “verde” en la ecuación N°52; proceso que se muestra en la siguiente imagen:
Imagen N°12: agrupación de resultados
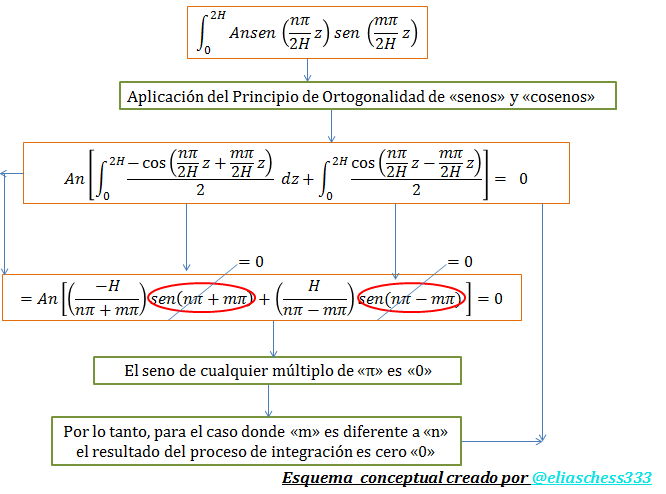
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Se tiene por lo tanto, que el caso donde “m≠n” no contribuye a encontrar el coeficiente “An” dado que el resultado del proceso de integración es cero.
• RESOLVIENDO LA INTEGRAL RESALTADA EN COLOR “VERDE” PARA “n=m”
En el esquema conceptual de la imagen N°13 se rescribe esta integral:
Imagen N°13: rescribiendo la integral resaltada en color "verde" (Ec.52), caso “n=m”
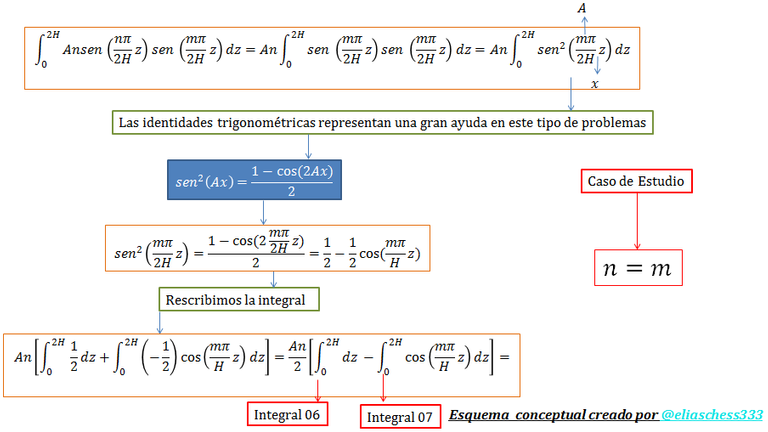
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
La solución de las “integrales 06 y 07” se presenta a continuación:
Imagen N°14: resolución de las integrales 06 y 07
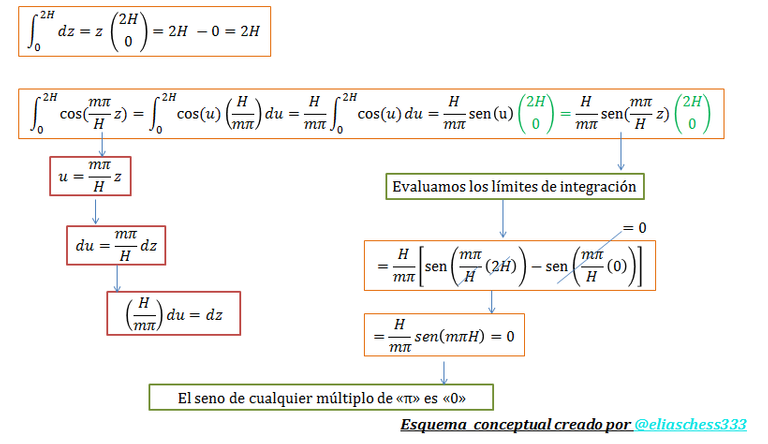
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Finalmente los resultados de las “integrales 06 y 07” se sustituyen en la integral resaltada en color “verde” de la ecuación N°52, obteniendo lo siguiente:
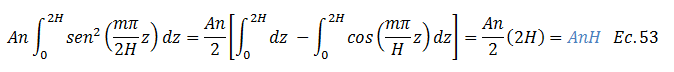
• ENCONTRANDO EL VALOR DE LAS CONSTANTES DE INTEGRACIÓN
Sustituimos en la ecuación N°52 los resultados de integración, plasmados en el esquema conceptual de la imagen N°06 y de la ecuación N°53:
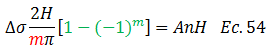
Analizando el término resaltado en color “verde” de la ecuación N°54:
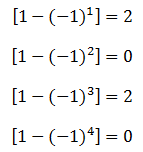
Se concluye por lo tanto que “An” tiene valor cuando “m” es impar, y el resultado en estos casos es dos. Este hecho permite rescribir la ecuación N°54:
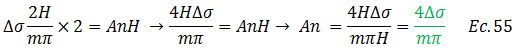
Y ASÍ LLEGAMOS A LA SOLUCIÓN ANALÍTICA DE LA ECUACIÓN DIFERENCIAL
Para tal fin, sustituimos el resultado de “An” en la ecuación N°50
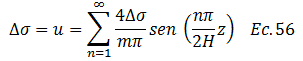
Rescribimos, tomando al mismo tiempo en consideración de que “n=m”
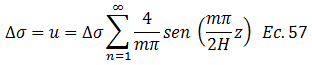
De acuerdo a lo planteado en líneas anteriores, es necesario que “m” sea un número impar, por lo tanto podemos establecer la siguiente ecuación:
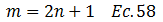
En este sentido la ecuación N°57 queda así:
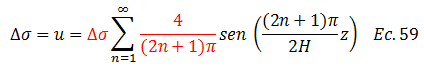
Se desprende así una nueva forma de presentar el valor de “An”, representada por el término resaltado por el color “rojo” de la ecuación N°59:
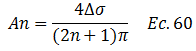
La ecuación N°59 está ajustada a la condición de borde N°02, donde para el instante de tiempo “t=0” el incremento de presiones “∆σ” producto de una carga externa aplicada, es igual al exceso de la presión a la hidrostática “u”. Para cualquier instante de tiempo, tenemos lo siguiente:
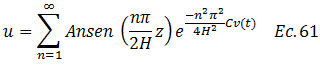
Partiendo del hecho de que “n=m” tenemos:
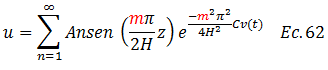
Sustituimos el valor de “An” dado en la ecuación N°60 y la forma de presentar “m” según ecuación N°58, llegando así a la solución analítica de la ecuación diferencial de la consolidación unidimensional de los suelos para flujo vertical:
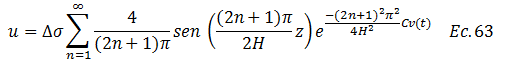
CONCLUSIONES
Al analizar detalladamente la solución de la ecuación diferencial en cuestión, se deducen las siguientes ideas:
1.- La variación de la presión en exceso a la hidrostática “u”, está influenciada por el coeficiente de consolidación “Cv”, el cual se encuentra vinculado a propiedades del suelo, como son la permeabilidad “k” y el coeficiente de variación volumétrica “mv”, es decir:
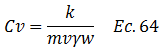
2.- La baja permeabilidad “k” de las arcillas, repercute directamente en el proceso de disipación de la presión en exceso a la hidrostática.
3.-El incremento de carga “∆σ” es en definitiva lo que propicia el surgimiento de la presión en exceso a la hidrostática “u”; si este valor es cero, esta última también tomará ese valor.
Teniendo la solución general de la ecuación diferencial del fenómeno de consolidación de los suelos, el reto es deducir expresiones de interés que contribuyan al tratamiento de la data obtenida a partir de la realización de este ensayo en un laboratorio de Mecánica de Suelos. En una próxima entrega, profundizaré en este aspecto.
Escribió para ustedes:
FUENTES DE INFORMACIÓN CONSULTADAS
1.- BADILLO J. Y RODRÍGUEZ R. 2007. MECÁNICA DE SUELOS TOMO I. FUNDAMENTOS DE LA MECÁNICA DE SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES
2.- BADILLO J. Y RODRÍGUEZ R. 1995. MECÁNICA DE SUELOS TOMO III. FLUJO DE AGUA EN LOS SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES
3.- SIMMONS G.Y ROBERTSON J.1993. ECUACIONES DIFERENCIALES CON APLICACIONES Y NOTAS HISTÓRICAS. SEUNDA EDICIÓN. McGRAW-HILL
LECTURAS RECOMENDADAS
4.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE MATEMÁTICO CON BASAMENTO EN EL PRINCIPIO DE ESFUERZOS EFECTIVOS Y LA LEY DE PERMEABILIDAD DE DARCY. PARTE I. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/ozrzfpbw
Saludos estimado @eliaschess333. Me encanta el enfoque que le das al uso de las matemáticas, dandole un sentido físico a una ecuación diferencial. De verdad que es un gran post.
Compañero @djredimi2, es muy interesante cuando le damos aplicabilidad a las matemáticas para la comprensión de los fenómenos físicos que ocurren a nuestro alrededor. Gracias por el apoyo @djredimi2. Saludos!
Deberías pertenecer al grupo de física jajaja. Hay mucha física en tus posts!
Es un honor la invitación, estoy seguro que aprenderé mucho de ustedes!
Excelente amigo como siempre y la importancia de la ecuación de fourier que tiene y sus distintas aplicaciones , me recuerda cuando me toco ver calculo 5 en la universidad
De acuerdo contigo, son muchas las aplicaciones de las series de Fourier; por ejemplo a través del uso de las mismas, se logró encontrar el valor de las constantes arbitrarias de integración del problema en estudio. Agradecido por el apoyo @gerardoalfred Saludos compañero!
Hi @eliaschess333!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV