Hello friends, after a long time without being able to publish product of my daily work, today I want to make reference in this publication to a content of great importance for physics, it is about Newton's laws, said laws I consider particularly that science changed physical, since through knowledge of these three newton laws were able to give results to problems that mathematically had no previous solutions, newton with these laws allowed to give meaning to the dynamics of bodies in motion, also also allowed to know the force of action and reaction that can exist in bodies. In this interesting publication you can observe a great content referring to the physical laws of Newton, I invite you to see this article.

Source
https://pixabay.com

What are Newton's Laws?

Newton's Laws, also known as Newton's Laws of Motion, 1 are three principles from which most of the problems posed by dynamics are explained, particularly those related to the movement of bodies. They revolutionized the basic concepts of physics and the movement of bodies in the universe, while

They constitute the foundations not only of classical dynamics but also of classical physics in general. Although they include certain definitions and in a certain sense can be seen as axioms, Newton asserted that they were based on observations and quantitative experiments; certainly they can not be derived from other more basic relationships. The proof of its validity lies in its predictions ... The validity of these predictions was verified in each and every one of the cases for more than two centuries.

In particular, the relevance of these laws lies in two aspects:

• On the one hand, they constitute, together with Galileo's transformation, the basis of classical mechanics;
• On the other hand, by combining these laws with the Law of Universal Gravitation, Kepler's Laws about planetary motion can be deduced and explained.

Thus, Newton's Laws allow to explain both the movement of the stars, as well as the movements of the artificial projectiles created by the human being, as well as all the mechanical functioning of the machines.

His mathematical formulation was published by Isaac Newton in 1687 in his work Philosophiae Naturalis Principia Mathematica.

However, the dynamics of Newton, also called classical dynamics, is only fulfilled in the inertial reference systems; that is, it is only applicable to bodies whose speed is considerably distant from the speed of light (not approaching 300,000 km / s); The reason is that the closer a body is to reaching that speed (which would occur in non-inertial reference systems), the more likely it is that a series of phenomena called relativistic effects or fictitious forces will affect it. they add supplementary terms capable of explaining the movement of a closed system of classical particles that interact with each other. The study of these effects (increase of the mass and contraction of the length, fundamentally) corresponds to the theory of special relativity, enunciated by Albert Einstein in 1905.

Laws

In a generalized way, the 3 laws of Sir Isaac Newton are:

First Law or Law of Inertia

Every body remains in its state of rest or uniform rectilinear motion unless other bodies act on it.

Second Law or Fundamental Principle of Dynamics

The force acting on a body is directly proportional to its acceleration.

Third law or Principle of action-reaction

When a body exerts a force on another, it exerts on the first an equal force and of opposite direction.

First Law or Law of Inertia

The first law of movement rejects the Aristotelian idea that a body can only keep moving if a force is applied to it. Newton states that:

Every body perseveres in its state of rest or uniform and rectilinear movement unless it is forced to change its state by forces impressed on it.

Newton's first law, also known as the Law of Inertia, tells us that if one body does not act another, it will remain indefinitely moving in a straight line with constant speed (including the state of rest, which equals zero speed).

As we know, movement is relative, that is, it depends on which observer describes the movement.

Thus, for a passenger on a train, the controller comes walking slowly down the train aisle, while for someone who sees the train passing from the platform of a station, the controller is moving at a great speed. Therefore, a reference system is needed to which to refer the movement.

Newton's first law serves to define a special type of reference systems known as inertial reference systems, which are those reference systems from which it is observed that a body over which no net force acts moves with constant velocity.

Source
https://pixabay.com

Concisely, this law postulates that a body can not change its initial state by itself, either at rest or in a uniform rectilinear movement, unless a force or a series of forces is applied, the result of which is not null on it. .

Newton thus takes into account the fact that moving bodies are constantly subjected to forces of friction or friction, which slows them down progressively, something new with respect to previous conceptions that understood that the movement or detention of a body was exclusively due if a force was exerted on them, but never understanding how it is to friction.

Consequently, a body with uniform rectilinear motion implies that there is no net external force, or in other words, a moving object does not stop naturally if a force is not applied to it. In the case of bodies at rest, it is understood that their speed is zero, so if it changes it is because a net force has been exerted on that body.

In fact, it is impossible to find an inertial reference system, since there is always some kind of force acting on the bodies, but it is always possible to find a reference system in which the problem we are studying can be treated as if we were in a inertial system. In many cases, assuming a fixed observer on Earth is a good approximation of the inertial system.

Below is a practical video of that, which explains in detail the first law of Newton :

Newton's Second Law or Law of Force

Newton's second law of motion says that

the movement change is proportional to the printed driving force and occurs according to the straight line along which that force is printed.

Newton's First Law tells us that for a body to alter its movement it is necessary that there is something that causes this change. That something is what we know as forces. These are the result of the action of some bodies on others.

Newton's Second Law is responsible for quantifying the concept of force. It tells us that the net force applied to a body is proportional to the acceleration that the body acquires. The constant of proportionality is the mass of the body, so that we can express the relationship in the following way:

F = m a

Both force and acceleration are vector magnitudes, that is, they have, in addition to a value, a direction and a direction. In this way, Newton's Second Law should be expressed as:

F = m a

The unit of force in the International System is the Newton and is represented by N. A Newton is the force that must be exerted on a body of one kilogram of mass so that it acquires an acceleration of 1 m / s2, that is,

1 N = 1 Kg · 1 m / s2

Source
https://pixabay.com

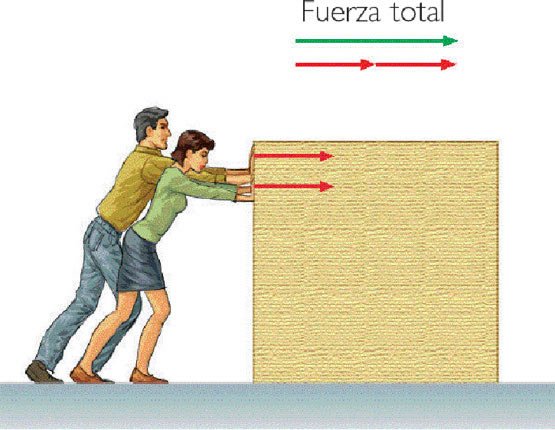
The expression of Newton's Second Law that we have given is valid for bodies whose mass is constant. If the mass varies, such as a rocket burning fuel, the relation F = m · a is not valid. We are going to generalize Newton's Second Law to include the case of systems in which the mass can vary.

For this we will first define a new physical magnitude. This physical quantity is the amount of movement that is represented by the letter p and that is defined as the product of the mass of a body by its speed, that is to say:

p = m · v

The amount of movement is also known as linear momentum. It is a vector magnitude and, in the International System, it is measured in Kg · m / s. In terms of this new physical magnitude, Newton's Second Law is expressed as follows:

The Force that acts on a body is equal to the temporal variation of the amount of movement of that body, that is,

F = dp / dt

In this way we also include the case of bodies whose mass is not constant. For the case that the mass is constant, remembering the definition of momentum and how a product is derived we have:

F = d (m · v) / dt = m · dv / dt + dm / dt · v

Since the dough is constant

dm / dt = 0

and remembering the definition of acceleration, we have left

F = m a

As we had seen previously.

Another consequence of expressing Newton's Second Law using the amount of movement is what is known as the principle of conservation of momentum. If the total force acting on a body is zero, Newton's Second Law tells us that:

0 = dp / dt

that is, that the derivative of the momentum with respect to time is zero. This means that the momentum must be constant over time (the derivative of a constant is zero). This is the principle of conservation of momentum: if the total force acting on a body is zero, the amount of movement of the body remains constant over time.

This law explains what happens if a moving body (whose mass does not have to be constant) acts a net force: the force will change the state of motion, changing the speed in module or direction. In particular, the changes experienced in the amount of movement of a body are proportional to the motive force and develop in the direction of it; that is, forces are causes that produce accelerations in bodies.

Consequently, there is a relationship between cause and effect, that is, force and acceleration are related. Synthetically stated, force is defined simply as a function of the moment in which it is applied to an object, with which two forces will be equal if they cause the same rate of change at the moment of the object.

In mathematical terms this law is expressed through the relationship:

Source
https://pixabay.com

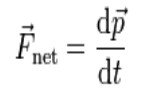
That is, the relationship between the force applied to the body and the acceleration obtained. When a body has a great resistance to change its acceleration (a large mass) it is said to have a lot of inertia. It is for this reason that the mass is defined as a measure of the inertia of the body.

Therefore, if the resultant force acting on a particle is not zero, this particle will have an acceleration proportional to the magnitude of the resultant and in the direction of it. The previous expression thus established is valid for both classical mechanics and relativistic mechanics, even though the definition of linear momentum is different in the two theories: whereas classical dynamics affirms that the mass of a body is always the same , regardless of the speed with which it moves, relativistic mechanics establishes that the mass of a body increases as the speed with which that body moves increases.

From the fundamental equation the definition of the unit of force or newton (N) is also derived. If the mass and acceleration are worth 1, the force will also be worth 1; thus, the newton is the force that applied to a mass of one kilogram produces an acceleration of 1 m / s². It is understood that acceleration and force must have the same direction and meaning.

The importance of this equation lies above all in that it solves the problem of the dynamics of determining the kind of force that is needed to produce the different types of motion: uniform rectilinear (mru), uniform circular (mcu) and uniformly accelerated (mrua) .

If many forces act on the body, the sum vector of all these forces must first be determined. Finally, if it were an object falling to the ground with an air resistance equal to zero, the force would be its weight, which would cause a descending acceleration equal to that of gravity.

Below is a practical video of that, which explains in detail the second law of Newton :

Third Law of Newton or Law of action and reaction

With every action there is always an equal and opposite reaction: that is, the mutual actions of two bodies are always the same and directed in the opposite direction.

The third law is completely original of Newton (since the first two had already been proposed in other ways by Galileo, Hooke and Huygens) and makes the laws of mechanics a logical and complete set. It states that for each force acting on a body, it performs a force of equal intensity and direction, but in the opposite direction on the body that produced it. In other words, the forces, located on the same line, always appear in pairs of equal magnitude and opposite in sense.

As we discussed at the beginning of Newton's Second Law, the forces are the result of the action of some bodies on others.

The third law, also known as the Principle of action and reaction essentially tells us that if a body A exercises an action on another body B, it performs on A another equal and opposite action.

Source
https://pixabay.com

This principle assumes that the interaction between two particles propagates instantaneously in space (which would require infinite speed), and in its original formulation is not valid for electromagnetic forces since they do not propagate through space instantaneously but they do at finite speed "c".

It is important to note that this principle of action and reaction relates two forces that are not applied to the same body, producing in them different accelerations, depending on their masses. For the rest, each of these forces obeys the second law separately. Together with the previous laws, this allows to enunciate the principles of conservation of linear moment and angular momentum.

This law is something that we can check daily on numerous occasions. For example, when we want to jump up, we push the ground to propel ourselves. The reaction of the soil is what makes us jump up.

When we are in a pool and push someone, we also move in the opposite direction. This is due to the reaction the other person makes to us, even if he does not try to push us.

It should be noted that although the pairs of action and reaction have the same value and contrary senses, they do not cancel each other out, since they act on different bodies.

Below is a practical video of that, which explains in detail the third law of Newton :

Bibliography :

• Physical laws, terrestrial dynamic movements .2015 .Ivvanny M.Douglas W.
• https://www.britannica.com/science/dynamics-physics
• https://en.wikipedia.org/wiki/Rigid_body_dynamics
• Isaac Newton, physical laws, mathematical analysis of bodies in motion. 2016.Yercherf K. Pabloch R.
• https://www.britannica.com/science/Newtons-laws-of-motion
• https://www.livescience.com/46558-laws-of-motion.html