
The Fourier transform, named after Jean-Baptiste Joseph Fourier (French mathematician who lived between 1768 and 1830), is an almost magical mathematical tool, capable of decomposing any periodic function (in time, or space) into a sum of functions of base of sinusoidal type (dependent of the frequency), or similar way to how a musical chord can be expressed in terms of the amplitudes (= volume) of each one its constituent notes.
The term Fourier transform refers not only to the transformation operation itself but also to the function it produces.

A good example is what the human ear does since it receives an auditory wave and transforms it, decomposing it into different frequencies (which is what is finally heard). The human ear perceives different frequencies as time passes, however, the Fourier transform contains all the frequencies of the time during which the signal existed; that is, in the Fourier transform a single frequency spectrum is obtained for the entire function. In short, the Fourier transform of a periodic function in time is basically the frequency spectrum of that function.
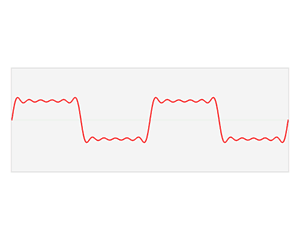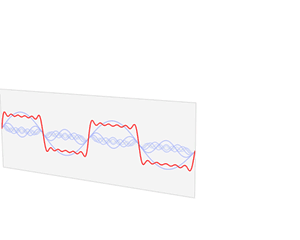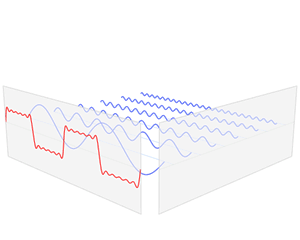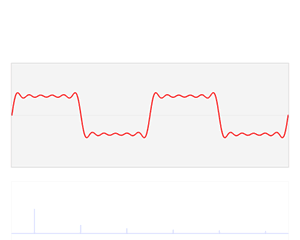
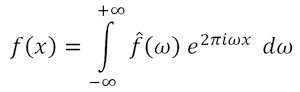
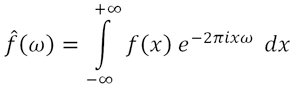
Each of these basic functions in which a function can be decomposed is a complex exponential with a different frequency (ω). Therefore, the Fourier transform provides us with a unique way of expressing any complicated function as the sum of simple sinusoids.
The inverse function to a Fourier transform is called inverse Fourier transform, also known as Fourier synthesis (or Fourier series), which is the way by which we can obtain any original periodic function from the sum of simple sinusoids
References
- https://en.wikipedia.org/wiki/Fourier_series
- https://brilliant.org/wiki/fourier-series/
- Fourier series, G. P. Tolstov

Hello,
We have found similar content: http://www.xtal.iqfr.csic.es/Cristalografia/parte_05_6.html
Not indicating that the content you post including translations, spun, or re-written articles are not your original work could be seen as plagiarism.
These are some tips on how to share content and add value:
Repeated plagiarized posts are considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
If you are actually the original author, please do reply to let us know!
Thank You.
More Info: Abuse Guide - 2017.
Fourier was an amazing genius to formulate that into simple equations.
What program was used to create the nice steemstem atom?
Being A SteemStem Member
Congratulations @rickyxp! You received a personal award!
Click here to view your Board
Congratulations @rickyxp! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!