In my previous post, we discussed the principles of mechanical resonance. In this post, we'll look into another vibratory characteristic called "beats", which can also be described by our undamped, mass-spring model (Figure 1).
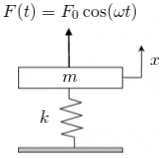
Figure 1. Undamped, forced oscillation mass-spring system.
What are beats?
Basically, beats occur due to the interference of two sound waves of slightly different frequencies. If you're a musician, you can hear beats when tuning instruments. If a note is out of tune, you will hear "wavering" or "fluttering" of the note. These are the beats.
Have a listen to the guitar being tuned via the link below. Two strings are plucked simultaneously (D string 5th fret; open G), but are slightly out of tune. Can you hear the beats?
Click here to listen to Guitar Tuning (source: WikiMedia Commons)
Beats can also occur when we excite the mechanical system (Figure 1) with vibrations that are close to its natural frequency. And this is what we're going to discuss in this post.
Let's look into the mathematics of beats in regards to our mass-spring system...
Beats
Equation (4) of the previous post (post #14) describes the general solution of the undamped mass-spring system. We'll label it as equation (1) here...
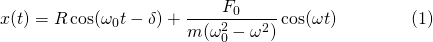
Now suppose that the conditions of the system are such that δ = 0 and x(0) = 0, then we find...

Thus the particular solution reduces to...

By the sum to product formulas (trigonometric identities), the term in the brackets can be expressed as...
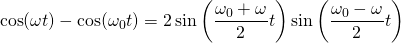
Substitute this into equation (2) and the particular solution becomes...

Equation (3) is the mathematical representation of beats.
So what occurs physically with our system?
When the input frequency (excitation frequency) ω is close to, but not quite equal to the natural frequency ω0, the mass m will bob up and down in the manner depicted graphically in Figure 2 below.
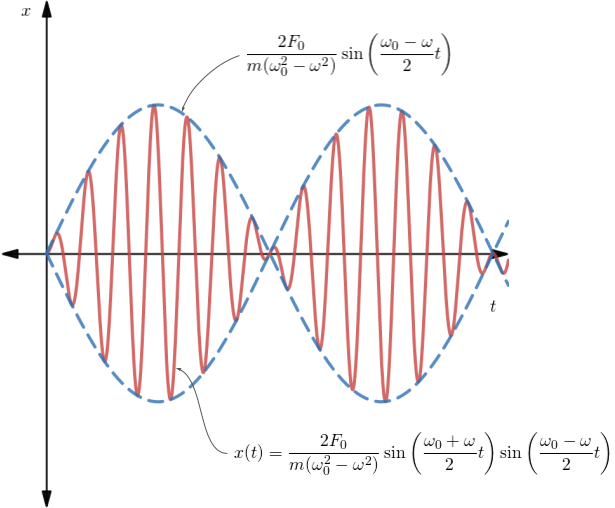
Figure 2. Response of the mass-spring system
Here's what I find fascinating about beats: the waveform is enveloped between the two large blue dashed sine waves. This sine waves have a frequency that is half of the difference between the natural frequency and excitation frequency...
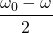
This is called the envelope frequency.
The frequency of the response (or sound) produced is the average of the natural and excitation frequencies...
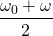
We see that within one cycle (one period) of the enveloping sine wave, there are 2 peaks in the modulating amplitude of the response. This is what we hear as beats. Thus the beat frequency is twice the envelope frequency, or...
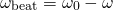
...which is simply the difference between the natural and excitation frequencies.
In the next post, we will see how the inclusion damping affects the response of the oscillating mass. Stay tuned.
Credits:
All equations in this tutorial were created with QuickLatex
Graphs are produced in desmos.com/calculator
First Order Differential Equations
- Introduction to Differential Equations - Part 1
- Differential Equations: Order and Linearity
- First-Order Differential Equations with Separable Variables - Example 1
- Separable Differential Equations - Example 2
- Modelling Exponential Growth of Bacteria with dy/dx = ky
- Modelling the Decay of Nuclear Medicine with dy/dx = -ky
- Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky
- Mixing Salt & Water with Separable Differential Equations
- How Newton's Law of Cooling cools your Champagne
- The Logistic Model for Population Growth
- Predicting World Population Growth with the Logistic Model - Part 1
- Predicting World Population Growth with the Logistic Model - Part 2
- What's faster? Going up or Coming Down?
First order Non-linear Differential Equations
- There's a hole in my bucket! Let's turn it into a cool Math problem!
- The Calculus of Hot Chocolate Pouring!
- Foxes hunting Bunnies: Population Modelling with the Predator-Prey Equations
Second Order Differential Equations
- Introduction to Second Order Differential Equations
- Finding a Basis for solutions of Second Order ODE's
- Roots of Homogeneous Second Order ODE's and the Nature their Solutions
- Modelling with Second Order ODE's: Undamped Free Oscillations
- Modelling Car Suspension with ODE's: Damped Free Oscillations Part 1
- Modelling Car Suspension with ODE's: Damped Free Oscillations Part 2
- Modelling Car Suspension with ODE's: Damped Free Oscillations Part 3
- Non-homogeneous Differential Equations
- Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 1
- Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 2
- Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 3
- Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 4
- Modelling Forced Oscillations with Second Order ODE's
- Second Order ODE's: Undamped forced oscillations: Resonance
- Second Order ODE's: Undamped forced oscillations: Beats
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Feel free to ask me any math question by commenting below and I will try to help you in future posts.
Visit my YouTube Channel at: https://www.youtube.com/masterwumathematics
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
That is a pretty fun example of beats :o)
It's a fascinating topic! :)
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
As a follower of @followforupvotes this post has been randomly selected and upvoted! Enjoy your upvote and have a great day!
It's fascinating. Oscillators can be used for so many things
Posted using Partiko Android
Congratulations @masterwu! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Hi @masterwu!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV