Perpendicular Distance from a Point to a Straight Line: Derivation of the Formula

In this post, we will use a bit of plane geometry and algebra to derive the formula for the perpendicular distance from a point to a line.

Now, the process I'm going to go through with you is not the most elegant, nor efficient, nor insightful. There's a lot of "ugly" algebra ahead.

But nonetheless, it is intuitive, and a perfectly valid way to derive the formula. In mathematics, there is often more than one way to do things and this is a perfect example of that. In future posts, we may use one of the more "elegant" methods.

Figure 1 below illustrates our problem...

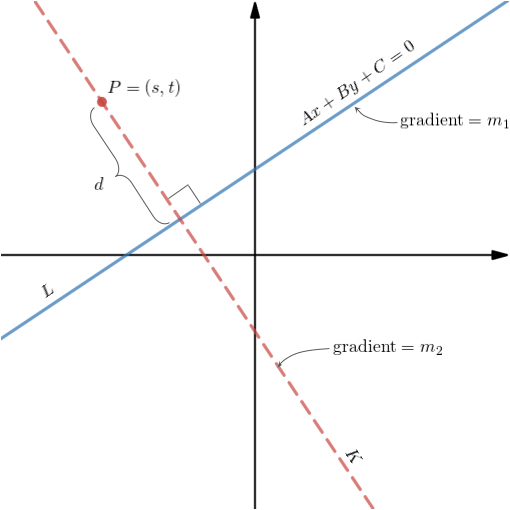
Figure 1. The perpendicular distance from a point to a line problem

In Euclidean Geometry, given the blue line L in standard form...

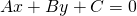
...and a fixed point P with coordinates (s, t), that is NOT on the line, the perpendicular distance d, or the shortest distance from the point to the line is given by...

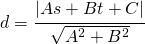
So how did this formula come about? Well, let's see - here is the outline of our approach...

1. Find the equation of a line K that coincides with the point P and intersects the line L at right-angles
2. Find the coordinates of the intersection point Q
3. Use the distance formula to find an expression for the distance between P and Q

Step 1. Equation of line K

First, let's rearrange the equation of the line L from the standard form into the "gradient-intercept" form...

Hence the gradient of the blue line is given by...

We can now find the gradient of the red dashed line K that is perpendicular to the blue line...

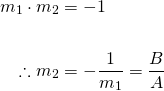
Now, using the "gradient-point" formula, with we can find the equation for the red dashed line...

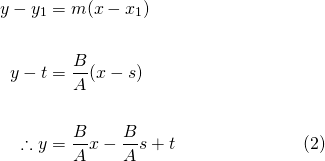
Step 2. Find the coordinates of Q

Let's now label the point at the intersection of the red dashed line K and the solid blue line L as Q. This is shown in Figure 2 below...

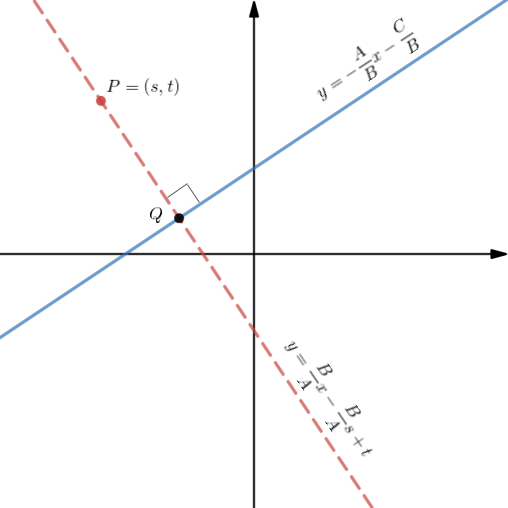
Figure 2. Finding the coordinates of the intersection point Q

I understand that it may be confusing to see an upward sloping blue solid line with a negatively labeled gradient, and a downward sloping red dashed line with a positively labeled gradient.

But remember, we are dealing with letters here. Numerically, they will definitely be the opposite and the correct way around.

I should have drawn the lines the other way around to avoid the confusion, so I apologise for the lack of foresight.

To find the coordinates of the intersection points Q, the two linear equations (1) and (2) must equal each other at that point. So we just solve them simultaneously...

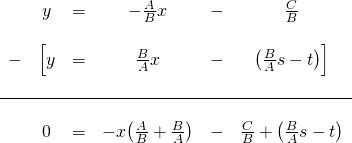
Solving for ...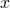

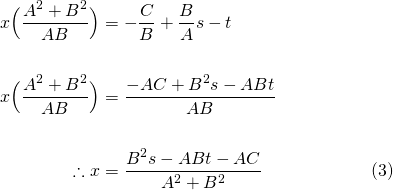
Substituting this result into (1) to solve for ...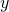

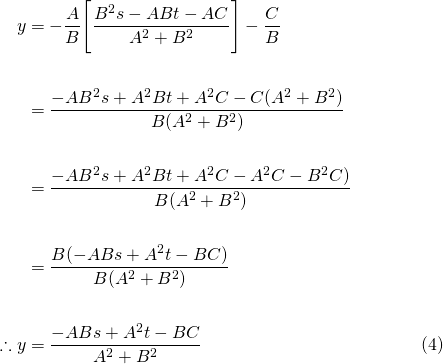
Therefore the coordinates of Q are...

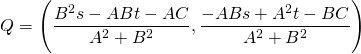
Step 3. Distance between P and Q

Now, the distance PQ is the perpendicular distance from the point P to the solid blue line L. This can be found via the "distance formula".

Here's some more ugly algebra...

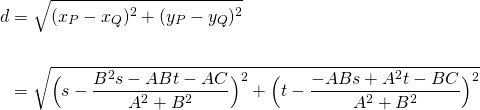
Let's simplify the first subtraction within the root first...

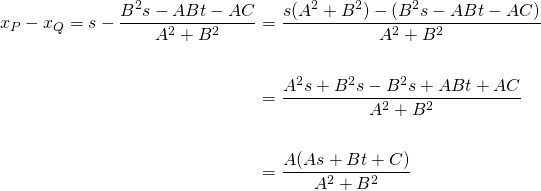
Now simplifying the second subtraction...

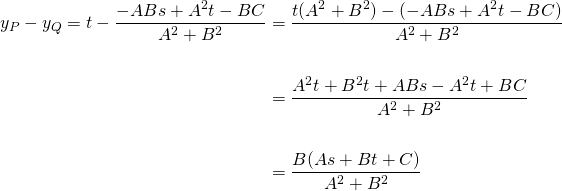
Substituting these into the distance formula, we get...

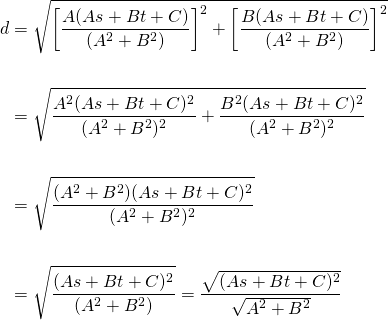
Now, the numerator term, 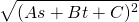, can be abbreviated to and thus we have derived the formula for the perpendicular distance from a point to a line:

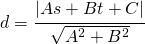
Ok, I hope you have enjoyed this post.

---

Credits:

All equations in this tutorial were created with QuickLatex

All graphs were created with www.desmos.com/calculator

---

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Feel free to ask me any math question by commenting below and I will try to help you in future posts.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3

Tip me at PayPal: https://paypal.me/MasterWu