Great to see people are enjoying these posts, thanks everyone who read and voted! In this part I'll get a bit more into the weeds of the simulation, and touch on the switch to Python.
A Random World History Simulator
To Recapitulate
Let me start by re-linking again the final video of part 2, showing the final results of the Excel VBA version of the sim:
Before leaving this version of the model behind for newer, Pythonian, pastures, I'd like to go into a bit more detail on the fundamental change that has so far lied at the basis of my simulation as radically distinct from the original model of the scientific article that was my impetus to build this simulation. (For more details on how the original model works, check parts 1 and 2!)
As I mentioned more briefly in part 2, the fundamental and radical change lay in changing how polity military power and stability are affected by polity size and ultra-sociality. I'm going to try my best to explain this, but you must forgive me that my math expertise is limited, so I might not be able to express properly what is happening mathematically. To compensate I've added a TL;DR after the math-heavy part to recap the most important point for the actual practical implementation in the simulation.
Maximum Curvature
The core of the simulation is now a crucial function, which I’ve nicknamed the Smax function. This function determines the relation between polity size and ultra-sociality, where the maximum size, Smax, is a function of the total number of ultra-social traits in the polity (i.e. the sum of all social traits in all tiles subject to the polity).
Put simply: for any given number of ultra-social traits, the Smax function gives a maximum number of tiles that a polity with that many ultra-social traits can hold.
There are some bells and whistles to it, but the fundamental shape of the Smax function is that of a root function, i.e. a half parabola with a vertical directrix. This means it initially increases rapidly, but then the rate of growth slowly diminishes.
What serves as the limiter to endless (if diminishing) Smax growth is that each tile has a maximum number of ultra-social traits it may contain. In my simulation this is 20.
This means that, even at maximum global ultra-sociality, there is a point where the result of the Smax function (the maximum number of tiles a polity can hold) becomes lower than the number of tiles required to attain the number of ultra-social traits required to get that Smax. This is the absolute upper bound of polity size. (If polity size = x, then when Smax(x * 20) = x that value of x is the absolute upper bound of polity size. Before that the value of Smax(x * 20) > x and after that the value of Smax(x * 20) < x.)
However, though there is a hard cap of a maximum of 20 ultra-social traits per tile, the simulation is still an evolutionary model where ultra-sociality in all tiles starts at 0 and slowly increases over time. Thus, at any point in time, in a specific area of tiles, there will be a mean ultra-sociality per tile, and this mean ultra-sociality determines the effective upper bound of polity size in that region of the world.
TL;DR: For any area of tiles, the Smax formula gives a maximum size in tiles that a polity in that area can grow to, where said maximum is based on the mean ultra-sociality of all tiles in that area.
How this is implemented, is that Smax forms the core of the other two crucial functions: military power and disintegration chance.
As mentioned before, the military power function is an upside-down parabola (an inverted U-shape). Smax determines its peak and where it drops below zero, with the latter being fairly close to Smax.
The disintegration chance is the random chance per step that a polity will disintegrate, i.e. collapse due to unspecified internal instability. This is another root function, which starts below zero and reaches 1 – c as polity size approaches Smax, where c is a constant. In the current sim this constant is 0.99, so at Smax size polities have a 1% chance of randomly collapsing each step.
If a polity grows above Smax size, the disintegration chance increases fairly rapidly. However, due to Smax determining both it and military power, polities don't simply grow till they disintegrate, because military power drops below zero well before disintegration chance approaches 100%.
This leads to the result you’re able to see in the video above. As ultra-sociality increases, polities are able to grow larger. Polities that find a local equilibrium remain at their effective maximum size for a while, but if they are not conquered by another polity they will eventually suffer from random collapse.
Partial to Disintegration
One new feature already added in the Excel version is that the disintegration that results from random chance is no longer total. Rather than the entire polity collapsing, only 80% of the polity’s tiles are made independent, the rest remaining as a now rump state which may attempt to reconquer its lost territory.
Here is an example of this happening in the video above, taken from around the year -370:
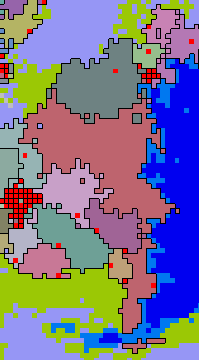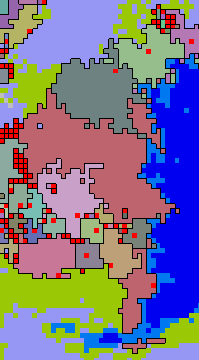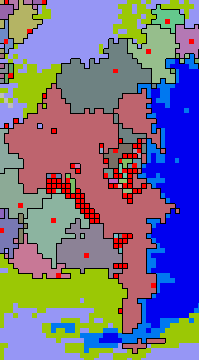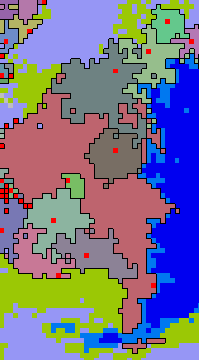
You are forgiven if you missed that, however, because states do still suffer total collapse regularly. In fact total collapse is considerably more frequent than partial collapse.
The reason is because when a polity loses its capital, it still suffers total collapse. And polities lose their capital a lot in this version of the sim.
Now, you may ask, didn’t I mention in the last post that how it was supposed to work is that as states lose far-flung territories, their military power increases again, thus they should be getting increasingly stronger as an enemy conqueror approaches the capital?
Yes, this was the intent. But what this sim is lacking is that polities are not ‘aware’ of the fact that they have capitals, let alone that these are existential weak points. Thus, when a polity loses tiles right next to their capital, they are as likely to use their now increased military power (due to lowered polity size when near maximum) to conquer more far-flung territories as they are to reconquer the tiles in their heartland.
This required fixing, but I’d reached the limits of what Excel could do. Rendering all the images of the video above via the makeshift Excel process took me a whole week, over a hundred hours, of constantly running the simulation. If I was going to iteratively improve and build on the simulation, I needed to be able to run it in a much smaller time frame, a day instead of a week. That, above any other concerns, made me decide to bite the bullet and learn how to port the sim to a better code base.
I spent some time putting this off, fearful of the amount of work it could take, but then a discord friend who is also a magnificent Python evangelist helped me by showing me exactly what libraries and functions I needed (mainly Numpy and Pillow) to port my VBA code into Python.
I would like to say that I turned the sim into a proper Python program. But I must confess this was definitely beyond me. The simulation is still fundamentally a form of procedural programming, with what is certainly some ‘unorthodox’ usage of Numpy arrays to mimic the behavior of arrays in VBA.
However, with every version I’ve been making more use of Python functions. For the first version after the Python port, I made use of lists to make polities prefer to conquer tiles close to their capitals when able. The result was the video below.
In addition to the increased stability, note how with Python handling the export to png, the images are now clean and proper, without whitespaces or borders. The time it took to simulate and render was a single night, more than an order of magnitude faster than the Excel process had taken for the video before!
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider using the steemstem.io app and/or including @steemstem in the list of beneficiaries of this post. This could yield a stronger support from SteemSTEM.
Congratulations @jd4e! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness to get one more award and increased upvotes!