Differential Equations Part 1: Introduction

Hello Friends of Steemit.

In this opportunity I write to make a small introduction on the differential equations.

The differential equations are very broad subject with many applications in different areas of science such as physics, chemistry, Biology, economics, sociology, etc.

Differential equations are considered advanced mathematics for science and engineering.

Already having an idea of how important they are, we will define that it is a differential equation.

A differential equation can be defined from the point of view of the,

Math: is an equation that relates a dependent variable or function and the derivative of this with respect to one or more independent variables (these are the parameters that make the function vary).

Example:

Equation 1

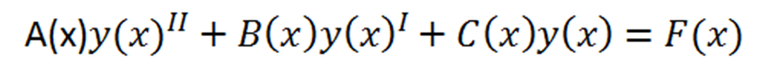
Physics: It is expressed as a mathematical model that pretends to reproduce or predict the behavior of a physical system, with physical system I mean any phenomenon of nature that we want to study the movement of a body, the transfer of heat, the Electrical conductivity to name a few.

Table 1

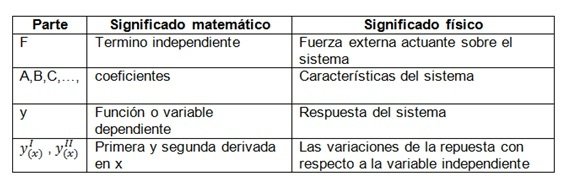
Having defined what they are: I will show you how they can be classified:

In the picture 1 we can see in an example the parts that make up a differential equation and in the 2 what represents each part mathematically and in the reality of a physical system,

Then a differential equation has:

ORDER: Is equal to the derivative of the highest order present in the equation. (shown in picture 1 is 2nd order).

Constant or variable coefficients: Depends on the values of a, B, C and whether these are constants or variables. (shown in image 1 has variable coefficients).

Grade: The degree of the differential equation will be the degree of the most order derivative. (shown in picture 1 is Grade 1).

Linear or non-linear: If the equation has Grade 1 and there are no products between the function and any of its derivatives then this is considered linear otherwise this will be nonlinear. (shown in picture 1 is linear).

Ordinary or partial: If the derivatives involved in the equation are total this will be ordinary, if the derivatives are partial the differential equation will be partial. (shown in image 1 is ordinary).

Homogeneous or non-homogeneous: If the independent term F is zero the equation will be homogeneous if f is different from zero then the equation will be non-homogeneous. (shown in picture 1 is homogeneous).

Newton's 2nd Law

which is most likely to be known and commonly stated as '' The Force equals mass by acceleration ''. is really a simplification of a differential equation.

Equation 2

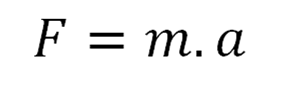
More generally, Newton's 2nd law states that the summation of forces exerted on a body is equal to the variation of momentum (amount of movement) with respect to time.

Equation 3

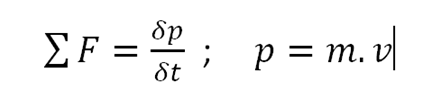
This is a non-homogeneous, linear, first-order, partial, first-degree differential equation.

Where momentum '' p '' is equal to the product of mass ‘’m’’ by speed ‘’v’’. That by considering the mass of the constant body can be expressed as a differential equation of second order, not homogeneous, with constant coefficients of first degree, linear, ordinary, as follows.

Equation 4

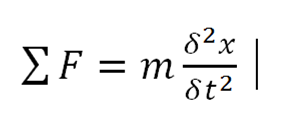
Example: Newton's second law would be used if we wanted to study the movement of a projectile launched from a cannon, this can be represented by an ordinary differential equation

source

In short if we are interested in studying some natural phenomenon, it is best to find a differential equation that represents it. Because through that equation you can even get to know the future behavior of the phenomenon studied.

Until here I came with this post, with which I wanted to introduce them in the world of differential equations, in future post will continue with the topic, I hope you like.

References.

Kreyszig, E. 1985, Advanced Mathematics for Engineering, 3rd edition, Tomo I, editorial.

Boyce, W; DiPrima, R. 2000, differential equations and problems with values in the Frontier, 4th edition, Editorial Mamusa.

Zill, D 1997, differential equations, with modeling applications, 6th editing.

https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_diferencial#Mec.C3.A1nica_cu.C3.A1ntica, 06-12-2017