Hello friends this is my first publication here in @steemstem, today I want to start a series that I have called Seismic Methods: starting with the introduction of this technique we will know what this method is about and what areas of studies it covers in science Seismic exploration methods are based on the generation of seismic waves, for example by means of an explosion or by means of a falling breaker. Seismic waves are mechanical and elastic waves, because seismic waves cause non-permanent deformations in the environment, in which they propagate. The deformation is constituted by an alternation of compression and expansion in such a way that the particles of the medium approach and move away, responding to the forces associated with the waves, as for example in an extended elastic. Its propagation is described by the wave equation. The speed of the seismic wave depends on the elastic parameters of the medium, in which the wave propagates.

image source:https://www.geovirtual2.cl
Elastic stress or strain (stress), strain (strain) and elastic constants
Stress S is defined as the force F per unit area A: F / A, where F is the force applied uniformly to a small surface area.
Pressure or traction refers to the tension directed perpendicular to the area, as it is exerted towards the body on which it acts (pressure) or in the opposite direction (traction). The pressure causes a shortening inside the body, in which it acts, the traction produces an elongation inside the body, in which it acts.
The longitudinal deformation εl is the ratio between the elongation or shortening Δl caused by a tension and the original length l before the application of tension: ε l = Δl / l. The transverse deformation ε a is defined as the relation between the variation of the width Δ a caused by a tension and the primitive width a of the body before the application of tension: ε a = Δ a / a.
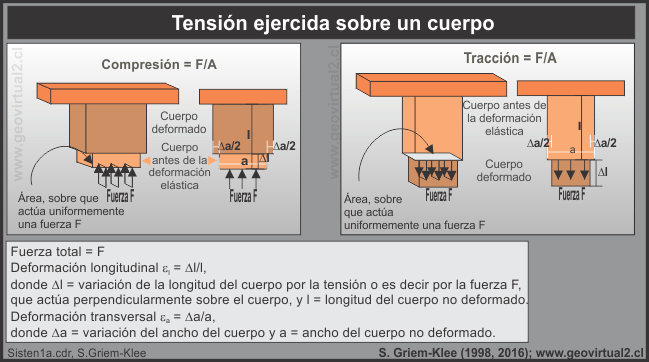
image source:https://www.geovirtual2.cl
Poisson's coefficient
When a body is shortened by compression, it stretches in the direction perpendicular to the compression. A body elongated by the effect of a traction, decreases its width in the direction perpendicular to the tension. The relation between the longitudinal deformation εl and the transverse deformation εa is called the Poisson's ratio σ.
σ = ε a / ε l = (Δ a / a) / (Δ l / l).
When a voltage acts on a body in one direction and the volume of the body is constant, the Poisson's coefficient has its maximum value equal to 0.5.
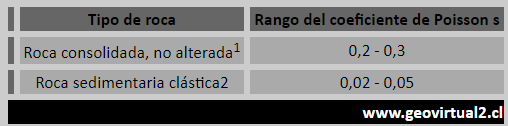
image source:https://www.geovirtual2.cl
1: For example fine-grained limestone, crystalline rocks.
2: Varying with porosity and weathering status.
Young E module
In the case of compressive or tensile stresses, which give rise to a small deformation, the magnitude of this deformation is proportional to the tension according to:
ε = k x S = (1 / E) x S → S = E x ε,
Module Young E, where
S = voltage
ε = deformation
E = proportionality constant and called the YOUNG module.
For a solid with a numerically high value YOUNG E module, the strain caused by a given voltage will be smaller compared to a solid of E of smaller value. (Values of E see table).
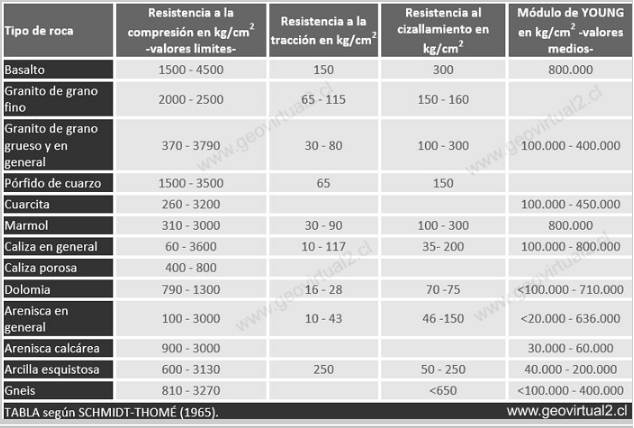
image source:https://www.geovirtual2.cl
Stiffness or shear modulus
The shear stress is called tension, which acts parallel to the area. The shear stress gives rise to a fracture deformation. The shear deformation is expressed by the deformation angle F. The angle of deformation is formed by the original surface of the area and the surface deformed by the tension exerted parallel to the area.
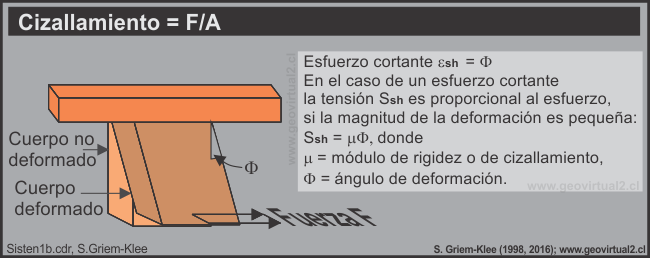
image source:https://www.geovirtual2.cl
In the case of a shear stress and a small deformation the tension Ssh is proportional to the deformation: Ssh = m 'f. In this relation m is the proportionality constant called the stiffness or shear modulus ɸ is the deformation angle. For liquids it is worth μ = 0, for most other materials μ approximately and numerically worth half of E.
Compressibility and volumetric module (see fig.)
Considering a body of volume V, which is subjected to a uniform compression force in all directions and consequently will decrease its volume by an amount ΔV, the compression exerted on this body is proportional to the deformation or that is to say the relationship between the variation of the volume and the primitive volume of this body before the application of compression according to: Scompression = k (ΔV / V), where the proportionality constant k is called compressibility. The reciprocal value of the compressibility 1 / k = k '= Scompression / (ΔV / V) is called the volumetric module.
There are the following relationships between the elastic constants introduced above:
μ = / [2 (1 + σ)] and k = E / [3 (1 - 2σ)],
compressibility see the following figure.
The seismic waves propagate in the solid substances in such a way that the deformation of the particles, which constitute the solid substance, pass through the substance with a velocity, which depends on their elastic properties and their density.
Deformation (strain) by dilatation
Deformation by dilation is the relation of the variation in the distance between two distinct and separate points (A and B), which is produced by a dilation movement, and the original distance between these two points.
Seismic waves
The internal seismic waves and the superficial seismic waves are distinguished.
The internal waves are:
● Waves for longitudinal waves or compression waves
● Waves or transverse waves or shear waves
The surface waves are for example:
● Love waves
● Rayleigh waves
Waves for longitudinal waves or compression waves
Particles of a p, longitudinal or compression wave oscillate in the direction of propagation of the wave. The p waves are similar to ordinary sound waves. The p waves are faster than the s waves or that is, after a tremor in an observatory the p waves arrive first, secondarily the s waves. The speed of the p waves is calculated as follows:

image source:https://www.geovirtual2.cl
Waves or transverse waves or shear waves
The particles of a s, transverse or shear wave oscillate perpendicular to the direction of propagation. We distinguish the sh waves, whose particles oscillate in the horizontal plane and perpendicular to the direction of propagation, and the sv waves, whose particles oscillate in the vertical plane and perpendicular to the direction of propagation. In polarized waves, its particles oscillate in a single plane perpendicular to its direction of propagation. The speed of the wave s is calculated as follows:

image source:https://www.geovirtual2.cl
Rayleigh waves
Rayleigh (1885) predicted the presence of surface waves by mathematically designing the motion of flat waves in a semi-elastic elastic space.
Rayleigh waves cause a rolling movement similar to sea waves and their particles move in ellipsoidal form in the vertical plane, which passes through the direction of propagation. On the surface the movement of the particles is retrograde with respect to the advance of the waves. The speed of the Rayleigh vRayleigh waves is less than the speed of the s waves (transverse) and is approximately vRaleigh = 0.9 'vs, according to DOBRIN (1988).
Love waves
Love (1911) discovered the surface wave, which bears his name studying the effect of elastic vibrations on a surface layer.
Love waves require the existence of a superficial layer of lower speed in comparison to the underlying formations or that is, a positive velocity gradient (speed increases) with depth. Love waves are shear waves, which oscillate only in the horizontal plane, that is, Love waves are horizontally polarized shear waves. The wave velocity of Love is approximately vLove = 0.9 x vs., according to Doyle, (1995).
The internal waves extend in three dimensions. The surface waves extend in only two dimensions. The speeds of the internal and surface waves are related as follows: vp> vs> vLove> vRayleigh. Generally for the amplitudes (A) of the waves the reverse order is valid: ARayleigh> ALove> As> Ap. As the amplitudes of the surface waves are decreased with the depth of focus, the ratio between the amplitudes of the surface waves and the amplitudes of the internal waves indicates approximately the depth of the focus.
In comparison with the internal waves, the amplitudes of the surface waves decrease less rapidly with distance, consequently over long distances with respect to a tremor, the surface waves generate higher signals and dominate the records conserved in the seismograms.
Surface waves are characterized by scattering, or the speed of surface waves depends on their frequency and wavelength. The variation of velocity with frequency or wavelength is called dispersion. In a wave affected by dispersion different wavelengths propagate with different speeds appearing as a train of events, whose successive cycles are of increasing or decreasing periods.
Analyzing the dispersion of Rayleigh waves, the scientists obtained very useful information about the structure of the Earth's crust and the Earth's upper mantle. On the contrary, in the exploration by the method of seismic reflections Rayleigh waves are less useful, because they contribute appreciably to the background noise.
The characteristic parameters of the rocks, which are determined with seismic methods are the speed of the waves p and s, the coefficient of reflection, the density. Properties of the rocks, which influence these parameters are among others:
● Petrography, mineral content.
● Compactness status.
● Porosity = percentage or proportion of empty space (pores) in a rock.
● Filling of empty space or that is, pores such as air, water, oil, gas.
● Texture and structure of the rock.
● Temperature.
● Pressure.
A variation in one of these properties of the rock can be related for example with a boundary between two lithological strata, with a fault or a zone of faults, with a change in the filling of the porous space of the rock.
Velocities of the p waves and s of some rocks are presented in the following table:
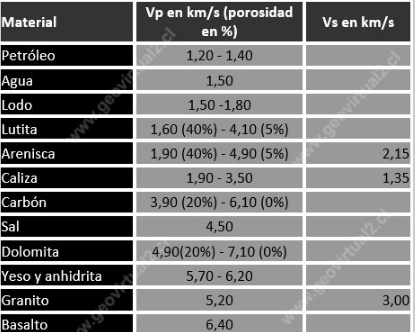
imagen source:https://www.geovirtual2.cl
The internal seismic waves such as the waves p and s are elastic waves, so that they are worth the laws of reflection and refraction. An incident seismic wave on a separation surface between two media such as two strata is partly reflected, partly refracted.
The internal seismic waves such as the waves p and s are elastic waves, so that they are worth the laws of reflection and refraction. An incident seismic wave on a separation surface between two media, such as two layers, is partly reflected, partly refracted. For reflection, the law of reflection is valid:

image source:https://www.geovirtual2.cl
When the angle of incidence reaches a critical value (Φ inc, so that sinΦ refraction = 90 °), a wave is generated, which propagates along the separation surface with the velocity of the wave corresponding to stratum2. This wave is called the MINTROP wave, according to Ludger Mintrop, a German, who in 1914 invented the first mechanical seismograph with sufficient precision for exploration.
In reflection and refraction phenomena, the two different seismic methods are based: the seismic refraction and the seismic reflections
The behavior and trajectory of seismic waves, which propagate in the subsoil can be presented:
● By a profile, which includes shot and several detectors (geophones) aligned on the earth's surface and which illustrates the penetration of wave fronts or wave beams respectively into the geological formations of the subsoil.
● For a graph of the time of the first arrival of the seismic wave as a function of the distance from the shot to the geophones, see distance-time graph.
Generating seismic waves artificially (mechanical vibrations or vibrations) at or near the surface and observing their arrival time at the observation stations (geophones) aligned along a profile, you can reconstruct the travel of the waves in the subsoil and locate discontinuities as lithological limits or faults.
Good friends of @steemstem I hope that this introductory content on the Seismic Exploration Method is of great interest to all of you I hope for your support, to continue publishing quality content then I will publish the topics that we will be talking about later as a continuation of this content:
2 . Elastic effort (stress)
3 . Deformation (strain)
4 . Elastic constants
5 . Seismic waves Behavior
Bibliography :
- Brown, Alistair R. (2004). Interpretation of three-dimensional seismic data (sixth ed.). Society of Exploration Geophysicists and American Association of Petroleum Geologists.
- Biondi, B. (2006). 3D seismic images: Three-dimensional seismic images. Exploration geophysical society.
- Claerbout, Jon F. (1976). Fundamentals of geophysical data processing. McGraw-Hill. ISBN 1-56080-137-9.
Ikelle, Luc T. and Lasse Amundsen (2005). Introduction to oil seismology. Exploration geophysical society. . - Scales, John (1997). Theory of seismic images. Golden, Colorado: Samizdat press. Archived from the original on August 18, 2015.
- Yilmaz, Öz (2001). Analysis of seismic data. Exploration geophysical society. .
- Milsom, J., University College of London (2005). Field geophysics Wiley Publications.
- Chapman, CH. (2004) Fundamentals of the Propagation of Seismic Waves. Press of the University of Cambridge.
References :
Grusic, V. and Orlic, M., early observations of rotating clouds by Andrija Mohorovičić, Bulletin of the American Meteorological Society, May 2007, p. 693-700, accessed January 4, 2010: [1]
W. M. Telford and others, Applied Geophysics (Cambridge Univ. Press, 1976) 220.
Sheriff, RE, and Geldart, LP, 1995, Seismology Exploration, Second Edition, Cambridge University Press, pp. 3-6.
EE Rosaire and Joseph H. Adler, "Applications and limitations of the immersion method", Bulletin of the American Association of Petroleum Geologists, January 1934, v.18 n.1 p.121.Sheriff, RE, Geldart, LP, (1995), 2nd Edition. Seismological Exploration. Press of the University of Cambridge.
"Physics and chemistry of the interior of the Earth - Seismic Reflection" (PDF). Retrieved on March 10, 2015.
Shuey, RT [1985] A simplification of the Zoeppritz equations. Geophysics, 50: 609-614
Avseth, P, T Mukerji and G Mavko (2005). Quantitative seismic interpretation. Cambridge University Press, Cambridge, p. 183
"Roll of earth". Schlumberger Oifield Glossary. Retrieved on September 8, 2013.
Zheng; Yingcai; et al. (2013). "Scholte waves generated by the topography of the eafloor s". arXiv: 1306.4383 freely accessible. Bibcode: 2013arXiv1306.4383Z.
"Reflection of multiples". Schlumberger Oifield Glossary. Retrieved on September 8, 2013.
You are always welcome to join us and get more recognition for your posts. You can find more information about geopolis here or join our Discord server.