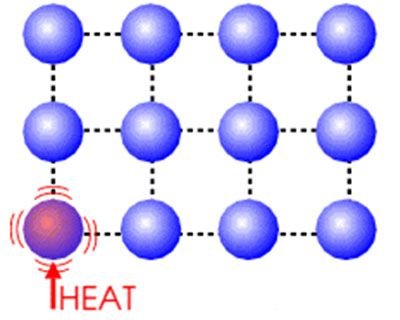
Hello friends of steemit, in this opportunity I want to talk about a subject that I consider very important for its technological applications, I refer to the transport phenomenons. Today we will talk about heat transfer.
Source
Heat transfer can be defined as the transmission of energy from one region to another, as a result of a temperature difference. Conduction, convection and thermal radiation represent the three mechanisms by which heat transfer occurs.
In conduction the transfer of heat is made through the material, without net mass flow, while in thermal radiation the bodies are separated in space and the change of thermal energy obeys the laws of electromagnetism.
The transfer of heat by conduction from a solid surface to a fluid in motion is known as heat transfer by convection.
In this first part, we will focus on the thermal conduction process, later, we will talk about convection and thermal radiation.
THERMAL CONDUCTION
Thermal conduction refers to the transfer of energy from the most energetic particles to the least energetic particles of a substance, due to the interactions between them. Higher temperatures are associated with higher molecular energies and when neighboring molecules collide, as they constantly do, a transfer of energy from the more energetic to the less energetic molecules must occur.
In the presence of a temperature gradient, the energy transfer per conduction must occur in the direction of the decreasing temperature.
In the conduction heat flow, the energy is transmitted by direct molecular communication (elastic shock in case of liquids) without appreciable displacement of the molecules.
The equations that describe this process are called Fourier Laws.
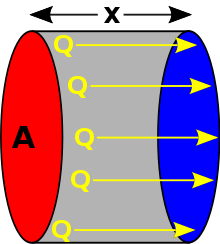
Heat flow in the decreasing direction of temperature
First Fourier Law
The first Fourier Law states that there is a proportionality between the flow of heat transfer by conduction (

) and the temperature gradient.
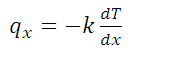 eq. (1)
eq. (1)
Where (

) is the heat flow per unit area in the spatial coordinates, which is established in the body due to temperature differences between two points of the same. The minus sign indicates that the flow is inverse to the direction of the gradient.
K is a constant characteristic called thermal conductivity.
Second Fourier Law: Energy Equation.
The energy equation can be found by considering the balance on a control volume and then differentially obtaining said equation, which is the following:
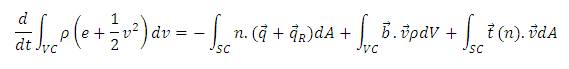 eq. (2)
eq. (2)
Where:
e is the energy.
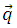 is the heat flow by conduction.
is the heat flow by conduction.
 is the flow of heat by radiation.
is the flow of heat by radiation.
The last two terms of the equation represent the power developed by the forces of body and surface.
The above equation states that the temporal change rate of the total energy of the control volume is equal to the net power developed by the force acting on the control volume, plus the net supply of energy that occurs across the surface of the control.
If we group the terms and apply the Gaussian divergence theorem, we obtain:
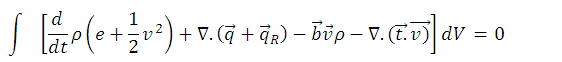 eq. (3)
eq. (3)
Since the volume is arbitrary (it is not zero), the integrand must be equal to zero. Combining with the continuity equation we obtain:
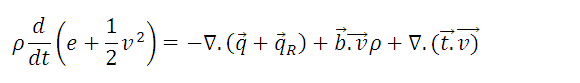 eq. (4)
eq. (4)
Where the mechanical energy comes from taking the scalar product between the velocity vector and the Cauchy equation:
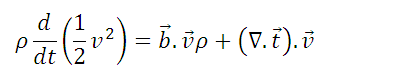 eq. (5)
eq. (5)
If we subtract the equations (4) and (5), where the stress tensor decomposes in pressure and viscous effort, we obtain:
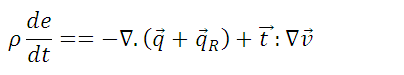 eq. (6)
eq. (6)
We can express this last equation in another way. If we introduce the enthalpy (

), after algebraic manipulations, we obtain the expression of the energy equation as a function of temperature, which is the following:
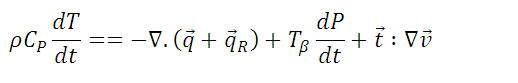 eq. (7)
eq. (7)
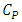 is the specific heat at constant pressure.
is the specific heat at constant pressure.
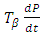 are the contributions of the terms of expansion and compression.
are the contributions of the terms of expansion and compression.
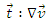 represents the viscous dissipation.
represents the viscous dissipation.

Source
Now, if we assume that the contributions of the terms of expansion and compression and viscous dissipation are small, and further that the terms of heat transfer by radiation and by convection are negligible, the above equation is considerably simplified.
Under these conditions and using the first Fourier law, we obtain the equation for conduction heat flow:
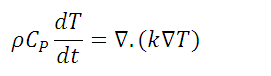 eq. (8)
eq. (8)
Which is called Second Fourier Law
References:
Nozad, I., Carbonell, R. G., and Whitaker, S. (1985). Heat conduction in multiphase systems: Theory and experiments for two-phase systems.
Bird, R.B. y Stewart, W.e., Lightfoot, E. N, 1996. Fenómenos de transporte, Reverté S.A., México D.C.
Welty, J. R.; wicks, C. E.; Wilson, R. E., (1984). Fundamentos de transferencia de momento, calor y masa. Edit. Limusa, México D.C.


 ) and the temperature gradient.
) and the temperature gradient. 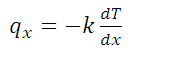 eq. (1)
eq. (1) ) is the heat flow per unit area in the spatial coordinates, which is established in the body due to temperature differences between two points of the same. The minus sign indicates that the flow is inverse to the direction of the gradient.
) is the heat flow per unit area in the spatial coordinates, which is established in the body due to temperature differences between two points of the same. The minus sign indicates that the flow is inverse to the direction of the gradient. 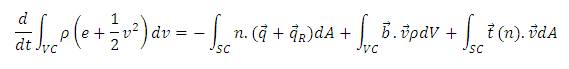 eq. (2)
eq. (2)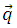 is the heat flow by conduction.
is the heat flow by conduction. is the flow of heat by radiation.
is the flow of heat by radiation.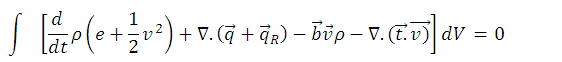 eq. (3)
eq. (3)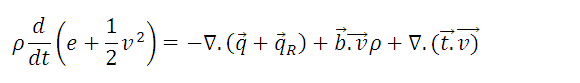 eq. (4)
eq. (4)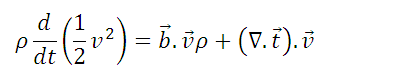 eq. (5)
eq. (5)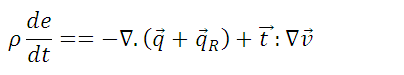 eq. (6)
eq. (6) ), after algebraic manipulations, we obtain the expression of the energy equation as a function of temperature, which is the following:
), after algebraic manipulations, we obtain the expression of the energy equation as a function of temperature, which is the following: 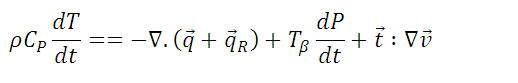 eq. (7)
eq. (7)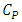 is the specific heat at constant pressure.
is the specific heat at constant pressure.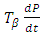 are the contributions of the terms of expansion and compression.
are the contributions of the terms of expansion and compression.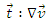 represents the viscous dissipation.
represents the viscous dissipation.
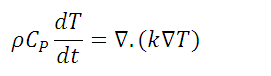 eq. (8)
eq. (8)
It is very curious that you study medicine and you are publishing about Physics and more if it deals with such complex topics as developing complicated equations that in my case is a kind of equations developed when I was very advanced in my career.
The publication is very good, but I am confused because it is totally opposite to what you study.
Hello @carloserp-2000, that I study medicine is not an impediment to interest me in other areas of science. When I finish my career, in a year, I intend to start studying physics and then specialize in biophysics.
I am especially interested in issues related to transport phenomena, as they may be directly related to medicine
I tell you that my favorite scientist is Adolf Fick. Fick was the one who described the diffusion process, which is a matter transport phenomenon very applicable to medicine. The interesting thing about all this is that Adolf Fick was not a physicist, a mathematician or a chemist. Fick was a doctor. Interesting!!
I hope I have clarified your confusion. I appreciate your comment.
Of course you can be interested in physics, but what you publish is complex, you must have a lot of knowledge of physics.
But if you have them well, you are free to publish what you want, I'm just confused, it should be easier for you to publish topics related to the area you study
Hello, I am very impressed with your publication. WOW, I just want to know what application transport phenomena can have in medicine, it's not my area and I do not know, but it's very interesting.
It is the curiosity of a fan of transport phenomena haha. Thanks friend