Uno de los puntos importantes que nos dejo como aprendizaje cuando estudiamos el tema de Interpolación Polinomial (1era, 2da, y 3era Parte) es que se debemos evitar interpolaciones polinomiales de alto orden en puntos igualmente espaciados. Esto puede suponer un problema si queremos producir un interpolador preciso en un intervalo grande [a, b]. Una forma de evitar esta dificultad es dividir el intervalo [a, b],

y posteriormente interpolamos la función dada en cada subintervalo de la forma [xi, xi+1] con un polinomio de orden bajo. Esta es la idea de interpolación polinómica a trozos. A los puntos xi se le llaman puntos de corte.
Iniciaremos estudiando la interpolación lineal a trozos, usando puntos de corte fijos y determinados por adaptación. Como las funciones lineales a trozos no tienen una primera derivada continua, y esto crea problemas en ciertas aplicaciones. Los interpolantes de Hermite cúbicos a trozos abordan este problema. En esta configuración, el valor del interpolador y su derivada se especifica en cada punto de corte. Los interpolantes cubículos locales se unen de una manera que fuerza la continuidad de la primera derivada. La continuidad de la segunda derivada se puede obtener mediante una selección cuidadosa de los valores de la primera derivada en los puntos de corte. Así, entramos en el tema de los splines, la cual es una idea muy importante en el área de aproximación e interpolación. Resulta que las splines cúbicos producen una solución más suave para el problema de interpolación.
Interpolación Lineal a Trozos
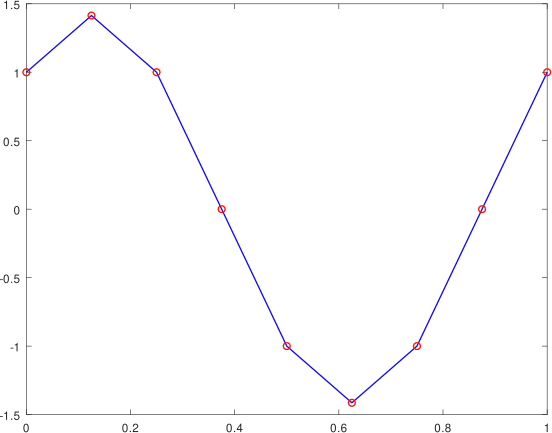
Supongamos que x(1: n) e y(1: n) son valores dados donde a = x1 < x2 < . . .< xn = b y yi = f(xi), con i = 1: n. Si conectamos los puntos (x1, y1), . . . , (xn, yn) con líneas rectas, como mostramos en la figura siguiente es la gráfica de una función lineal por partes.
Función lineal a trozos, elaboada en GNU Octave, por @abdulmath.
El interpolador lineal a trozos se basa en los interpolantes lineales locales siguientes

donde para i = 1: (n-1) los coeficientes están definido por
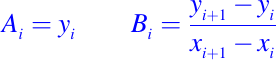
Notemos que Li(z) es simplemente el interpolador lineal de f en los puntos x = xi y x = xi + 1. Definamos
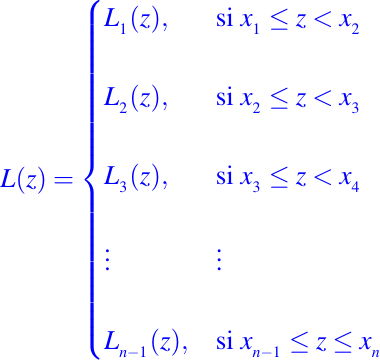
El hecho de configurar L es el hecho de resolver cada uno de los problemas de interpolación lineal local. Las n - 1 diferencias divididas B1, B2, . . . , Bn - 1 puede ser fácilmente calculadas por un bucle de la forma siguiente

o mediante el uso de división puntual,

o usando la función
diff de la forma siguiente:
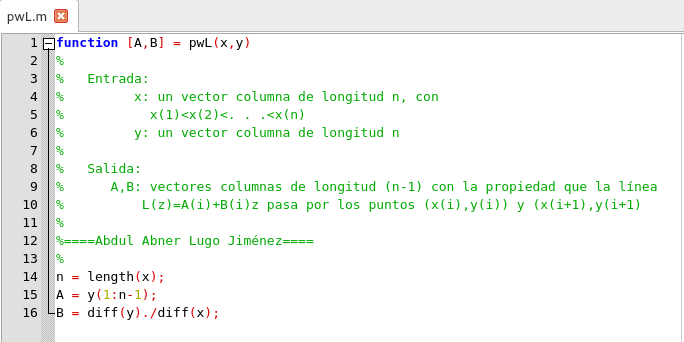
Usando algunas de estas operaciones podemos construir la siguiente función
Script de una Función de interpolación lineal a trozos, elaborada en GNU Octave, por @abdulmath.
Así, el siguiente script

establece un interpolador lineal por partes de la función

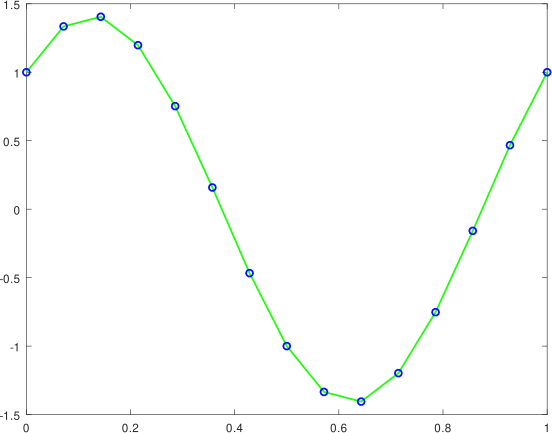
en una partición uniforme de 15 puntos del intervalo [0,1]. La gráfica la podemos ver a continuación.
Elaborada con GNU Octave, por @abdulmath.
Evaluación
Para evaluar L en un punto z del intervalo [a, b], es necesario determinar el subintervalo que contiene z. En nuestro problema x tiene la propiedad de que x1 < . . . < xn y por lo tanto sum(x <= z) es el número de xi que están a la izquierda de z o igual a z. Resulta que
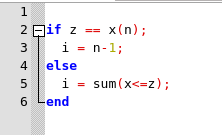
determina el índice i de modo que
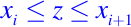
Observe el manejo especial del caso cuando z es igual a xn. Se realizarán un total de n comparaciones porque cada componente en x se compara con z.
Un mejor enfoque es explotar la monotonía de xi y usar la búsqueda binaria. Está es la idea principal.
Supongamos que tenemos índices Izq y Der tal que
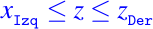
Si
medio=floor((Izq + Der)/2) entonces para chequear z con la relación xmedio podemos reducir a la mitad el espacio de búsqueda redefiniendo Izq oDer por lo tanto:
La aplicación repetida de este proceso finalmente identifica el subintervalo que contiene a z:
Script para determinar el índice i para localizar z. Elaborado en GNU Octave, por @abdulmath.
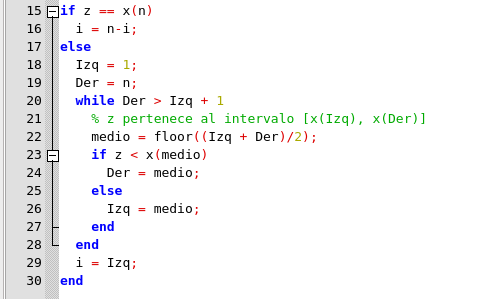
Al finalizar, i indica el índice del subintervalo que contiene a z. Si n = 10 y z pertenece al intervalo [x6, x7], entonces aquí está la sucesión de valores
Izq y Der producidos por el método de búsqueda binario:
Izq | Der | medio |
|---|---|---|
| 1 | 10 | 5 |
| 5 | 10 | 7 |
| 5 | 7 | 6 |
| 6 | 7 | - |
Aproximadamente log2(n) son las comparaciones necesarias para localizar el subintervalo apropiado. Si n es grande, entonces esto es mucho más eficiente que el método de sum(x<z), que requiere n comparaciones.
Para z aleatorio, no podemos hacer nada mejor que la búsqueda binaria. Sin embargo, si se va a evaluar L en una sucesión de puntos anotada, entonces podemos mejorar el proceso de ubicación del subintervalo. Por ejemplo, supongamos que queremos gráficar L en [a, b]. Esto requiere el ensamblaje de los valores L(z1), . . . , L(zm) en un vector donde m es un número entero generalmente grande y

En lugar de localizar cada zi mediante búsqueda binaria, es más eficiente explotar la migración sistemática del punto de evaluación a medida que se mueve de izquierda a derecha en los subintervalos. Lo más probable es que si i es el índice del subintervalo asociado con el valor z actual, entonces i será el índice correcto para el siguiente valor z. Esta conjetura de el subintervalo correcto se puede verificar antes de iniciar el proceso de búsqueda binaria.
Script de Localización optimizado, elaborado en GNU Octave, por @abdulmath.
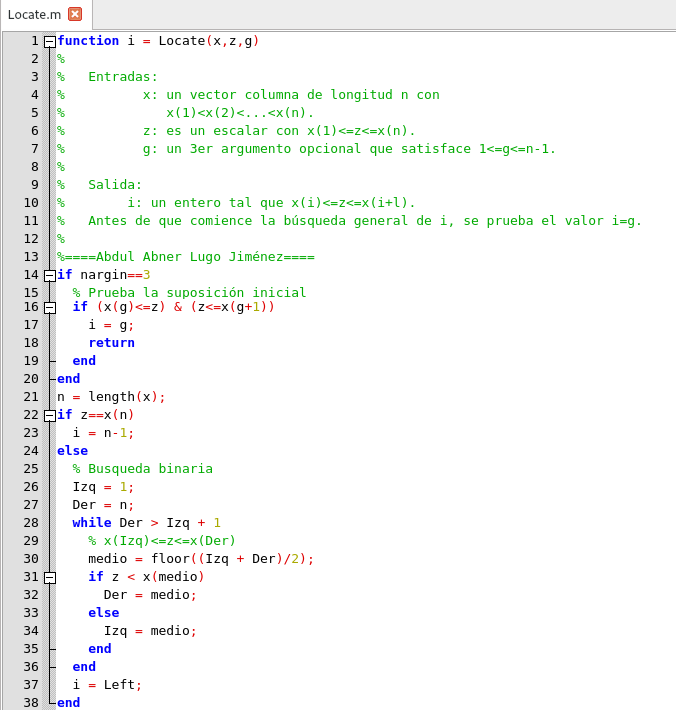
La función Locate hace uso del comando de return. Este termina la ejecución de la función. Es posible reestructurar la función Locate para evitar return pero la lógica resultante sería engorrosa. Como una aplicación de Locate aquí hay una función que produce un vector de L valores:
Script de función de aplicación. Elaborado en GNU Octave, por @abdulmath.
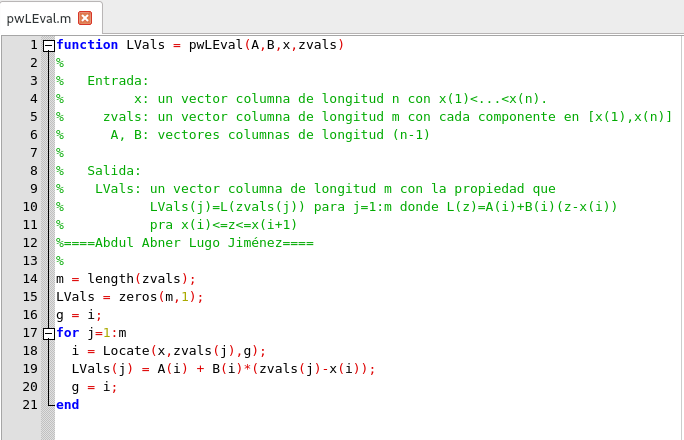
El siguiente script ilustra el uso de esta función, produciendo una secuencia de aproximaciones lineales a trozos a la función
Script de aplicación. Elaborado en GNU Octave, por @abdulmath.
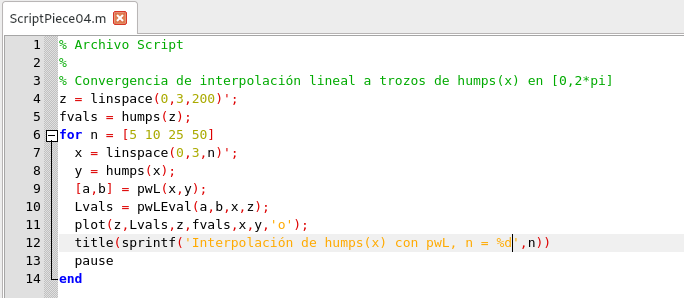
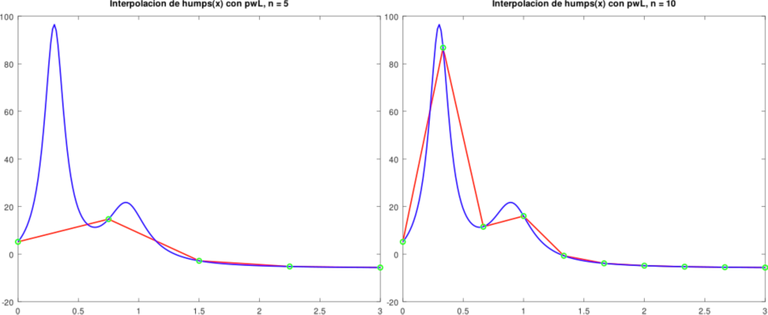
Observe que se requieren más puntos de interpolación en regiones donde las jorobas son particularmente no lineales.
Gráficas obtenidas de la Aplicación. Elaboradas con GNU Octave, por @abdulmath
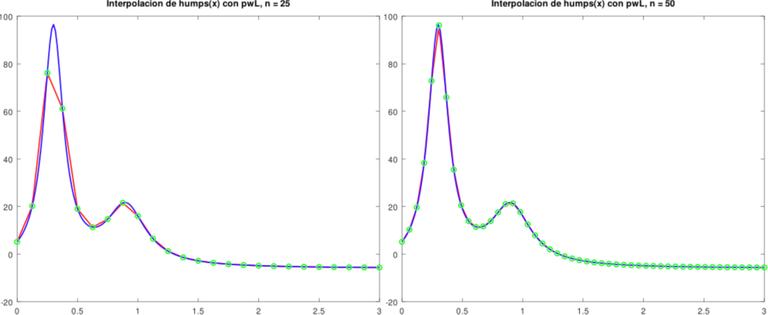
Determinación a Priori de los Puntos de Cortes
Consideremos cuántos puntos de corte necesitamos para obtener un interpolador lineal por partes satisfactorio. Si z pertenece al intervalo [xi, xi + 1], tenemos
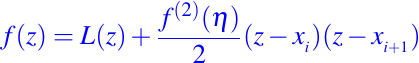
donde n pertenece al intervalo [xi, xi + 1]. Si la segunda derivada de f en [a, b] está acotada por M2 y si h es la longitud del subintervalo más largo de la partición, entonces no es difícil mostrar que
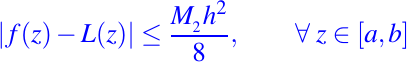
Una situación típica en la que se puede aprovechar esta cota del error es en el diseño de la partición subyacente en la que se basa L. Suponga que L(x) se basa en la partición uniforme

donde
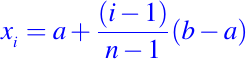
Para garantizar que el error entre L y f es menor o igual que una tolerancia positiva dada, insistimos que
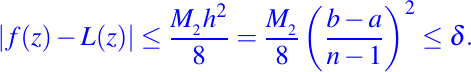
De esto concluimos que n debe satisfacer
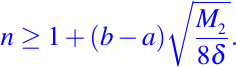
Por el motivo de la eficiencia, tiene sentido dejar que n sea el número entero más pequeño que satisface la desigualdad.
Script para construir la partición.Elaborado con GNU Octave, por @abdulmath
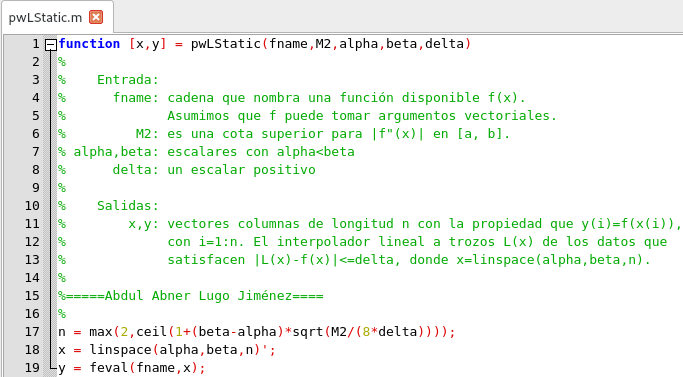
La partición producida por
pwLStatic no tiene en cuenta los valores muestreados de f. Como resultado, la partición uniforme producida puede ser demasiado refinada en regiones donde f'' es mucho más pequeña que la cota M2.
Interpolación Lineal a Trozos Adaptativa
Supongamos f no es muy lineal en una pequeña parte de [a, b] y es muy suave en otros lugares. (Comó pudimos observar en las gráficas anteriores.) Esto significa que si usamos pwLStatic para generar la partición, entonces estamos obligados a usar una cota M2 grande. Se necesitarán muchos subintervalos y f-evaluaciones. Sobre las regiones donde f es suave, la partición será demasiado refinada.
Para resolver este problema, desarrollamos un algoritmo de partición recursivo que encuantra dónde f es "no lineal" y eso agrupa los puntos de cortes en consecuencia. Una definición simplifica la discusión. Decimos que el subintervalo [xL, xR] es aceptable si
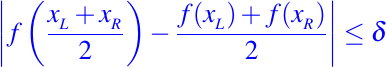
o si
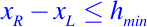
donde delta y hmin son positivos, se les conoce como los parámetros de refinamiento (típicamente pequeños).
La primera condición mide la discrepancia entre la línea que conecta (xL, f(xL)) y (xR, f(xR)) y la función f(x) en el punto medio del intervalo m = (xL + xR)/2.
La segunda condición dice que los subintervalos suficientemente pequeños también son aceptables cuando suficientemente pequeño significa menos de la longitud hmin.
Se requiere una definición más antes de que podamos describir el proceso de partición completo. Una partición x1 < x2 < . . . < xn es aceptable si cada subintervalo es aceptable. Tenga en cuenta que si

es una partición aceptable de [xL, m], y si

es una partición aceptable de [m, xR], entonces

es una partición aceptable de[xL, xR]. Esto establece el escenario para una determinación recursiva de partición aceptable.
Función para construcción de la partición recursiva. Elaborado en GNU Octave, por @abdulmath.
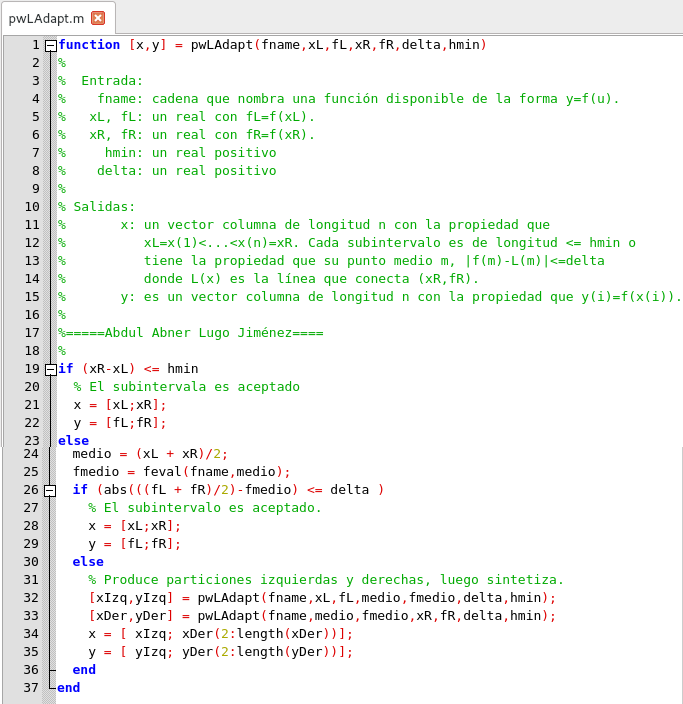
La idea detrás de la función es verificar y ver si el intervalo de entrada es aceptable. Si no lo es, las particiones aceptables se obtienen para los intervalos de la mitad izquierda y derecha. Luego se unen para obtener la partición final aceptable. La distinción entre interpolación lineal a trozos estática y adaptativa se revela mediante el siguiente script
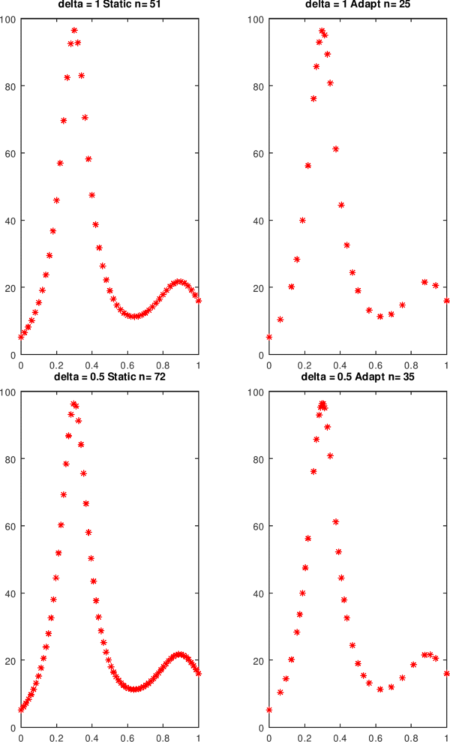
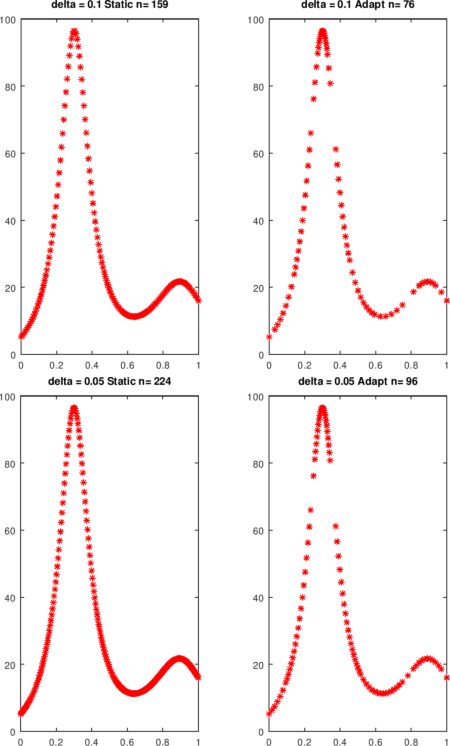
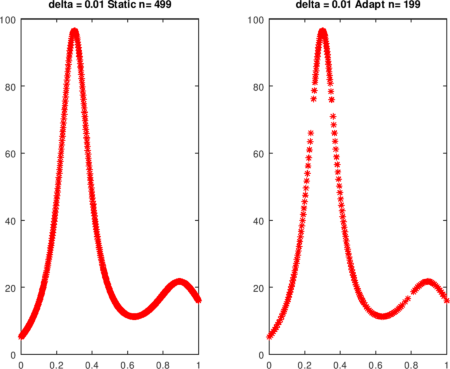
La función humps es muy no lineal en las proximidades de x = 0.3. La cota de la segunda derivada se aproxima con diferencias y se usa en pwLStatic. En el ejemplo, aproximadamente dos veces se requieren tantas evaluaciones de funciones cuando se toma el enfoque estático.
Queridos amigos y lectores, espero hayan disfrutado y aprendido acerca de la Interpolación Polinomial a Trozos usando el entorno GNU Octave | 1era Parte, de igual manera los invito para la 2da Parte de este tema, donde continuaremos mostrando el desarrollo del mismo con los script y aplicaciones. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
- Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
- Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.
Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave,  , GIMP e Inkscape.
, GIMP e Inkscape.
@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.
Imagen diseñada con GIMP y elaborada por @abdulmath.







¡Felicitaciones!
Apoya al trail de entropía y así podrás ganar recompensas de curación de forma automática, entra aquí para más información sobre nuestro TRAIL.
Puedes consultar el reporte diario de curación visitando @entropia
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias por la nominación y el apoyo.
Excelente trabajo, amigo.
Hola @kantos, que bueno que pudieras entender la idea que quise plasmar. Agradecido por todo. Saludos y un abrazo.
Bien organizado y estilizado en cuanto a su diagrama ... Felicidades.. Un abrazo...
Hola @eleazarvo, agradecido por tu valoración. Saludos y un abrazo.
Wuaooo..... Sin mucho que... Sin Comentarios, excelente
Gracias por pasar a leer un rato. Saludos.
Muy interesantes, de verdad toda una referencia en todo este campo, excelente presentación.
Agradecido por tu comentario @megaela, tu valoración es importante. Saludos cordiales.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thanks for the support
Impresionante post, excelente información.
Hola @andreacastaneda, gracias por leerlo y me agrada mucho que te gustará, espero pueda servirte de ayuda la información. Saludos
Hi @abdulmath!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks for the support
Congratulations @abdulmath! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard: