


La motivación principal del estudio del cálculo matricial, es poder resolver el problema de la ecuación lineal
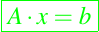
Sin embargo, antes de entrar en detalles algorítmicos de un problema que puede resultar complejo en algunos casos resolver, es importante estudiar parte del cálculo matricial, el cual podemos dividir en dos casos sencillos: el primero multiplicación de una matriz por un vector y segundo la multiplicación de una matriz por una matriz. Ambas operaciones están soportadas en Octave por lo que en ese sentido no hay mucho que hacer. Sin embargo, hay mucho que aprender al estudiar cómo se pueden implementar estos cálculos. Las multiplicaciones de una matriz por un vector surgen durante el estudio de la resolución de problemas de la forma
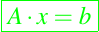
Adicionalmente, siempre es un buen consejo tratar de mejorar nuestras capacidades para este caso, antes de iniciar una presentación de como resolver este tipo de ecuaciones.
También es de hacer notar, que el problema matricial también merece prestarle mucha atención. Es frecuente, que el volumen de trabajo que se requiere para inicializar una matriz de orden n x n, puede ser tan grande, como que que se puede requerir para resolver el problema matricial. Es por ello, que es importante poner un poco de atención a la configuración de las entradas de la matriz, cuando esta puede ser la evaluación de una función continua f(x, y).
Una muy buena parte de este tema será el estudio y comprensión de la estructura de la matriz. Recurrentemente nos encontramos con el caso de patrones para los valores de las entradas, el cual puede ser usado para recudir el volumen de trabajo. Ejemplos de recursividad en los cálculos matriciales son: La transformación rápida de Fourier y el algoritmo de multiplicación rápida de la matriz de Strassen.

Antes de que un problema matricial pueda ser resuelto, debe ser configurado apropiadamente. En muchas aplicaciones, la cantidad de trabajo asociada con la fase de configuración compite con la cantidad de trabajo asociado con la fase de solución. Por lo tanto, nos interesa adquirir una intuición sobre esta actividad. También es una ocasión para ver el poder y capacidad del manejo vectorial de Octave al nivel matricial.

Si las entradas en una matriz A = (aij) se especifican mediante entradas simples, tales como
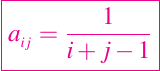
entonces un script de doble bucle puede ser usado para su cálculo:

Script para la construcción de una matriz con entrada simple. Elaborado en GNU Octave, por @abdulmath.
La preasignación con
zeros(n,n) reduce la sobrecarga de la gestión de la memoria.
A veces la matriz definida tiene patrones que pueden ser explotados. Si la matriz anterior es simétrica ya que aij = aji para todos los valores i y j, lo que significa que las entradas (i, j) sólo necesita ser aplicada la mitad de las veces:

Script para la construcción de una matriz simétrica. Elaborado en GNU Octave, por @abdulmath.
Este ejemplo particular es una matriz de Hilbert y sucede que hay una función incorporada A =hilb(n) que puede ser usado en lugar de los scripts anteriores. Para ello, el comando hilb muestra una implementación totalmente vectorizada, ya que la creación de una matriz puede ser más eficiente si se explotan las relaciones que existen entre las entradas.
Consideremos la construcción de la matriz triangular inferior de coeficientes binomiales:
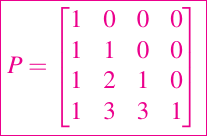
El coeficiente binomial de m elementos elegidos en grupos de k elementos se define como
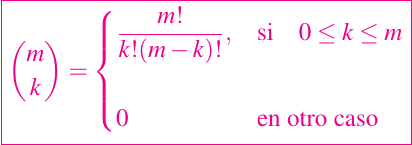
Si k es menor o igual a m, entonces especifica el número de formas en que los k elementos pueden ser seleccionados de un conjunto de m elementos. La entrada ij de la matriz que estamos configurando esta definida por
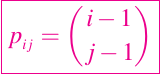
Si simplemente calculamos cada entrada usando la definición factorial, entonces O(n3) errores están involucrados. Por otro lado, en el caso de 5 por 5 se observa que P es triangular inferior con valor 1 en la diagonal y la primera columna. Una entrada que no se encuentra en estos lugares es la suma de sus vecinos del norte y del noroeste. Eso es,

Esto permite la siguiente estrategia de configuración:
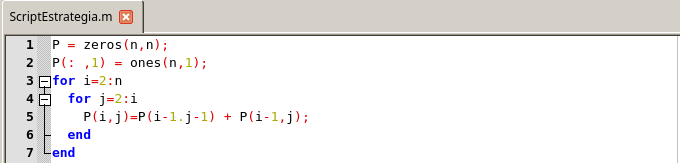
Script para la estrategia de configuración. Elaborado en GNU Octave, por @abdulmath.
Este script implica errores O(n2) y por lo tanto es un orden de magnitud más rápido que el método que ignora las conexiones entre los pij.

Muchas matrices se definen en términos de un vector de parámetros. Recordemos la matriz de Vandermonde dada por:
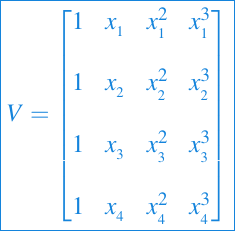
Podemos desarrollamos varias estrategias de configuración, pero aquí presentamos una en particular la cual es una técnica orientada a las columnas:
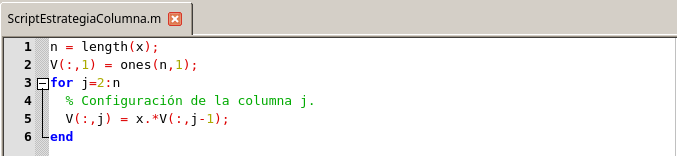
Script para la estrategia de configuración por columnas. Elaborado en GNU Octave, por @abdulmath.
Las matrices circulantes son también de este género, las cuales están definidas por un vector de parámetros. Por ejemplo
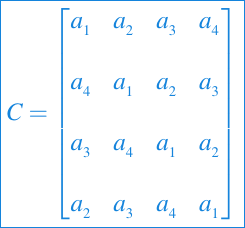
Cada fila de un circulante es una versión desplazada de la fila de arriba. Aquí hay dos funciones de configuración de la estrategia circulante:
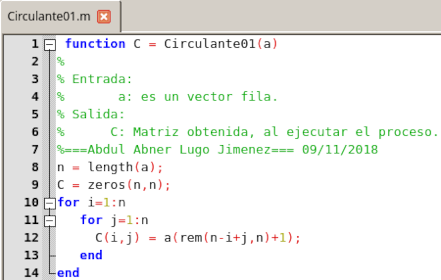 | 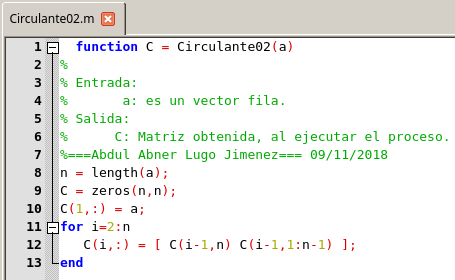 |
|---|---|
Función Circulante01. Elaborado en GNU Octave, por @abdulmath. | Función Circulante02. Elaborado en GNU Octave, por @abdulmath. |
La función Circulante01 explota el hecho de que cij= a((n-i+j)mod(n))+1, y que es una implementación a nivel escalar. La función Circulante02 explota el hecho de que C(i, :) es un desplazamiento a la izquierda de C(i - 1, :) y es una implementación a nivel vectorial. En Octave esta última función es es mucho más eficiente, lo cual lo podemos visualizar al ejecutar el siguiente Script:
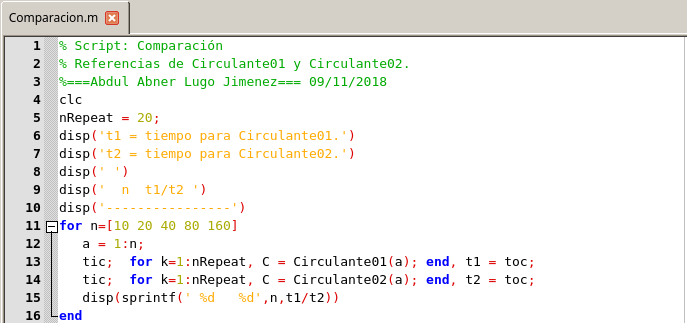
Script de comparación de tiempo de ejecución. Elaborado en GNU Octave, por @abdulmath.
| n | t1/t2 |
|---|---|
| 10 | 7.44504 |
| 20 | 14.6228 |
| 40 | 28.0112 |
| 80 | 59.5192 |
| 160 | 109.635 |
t1: Tiempo Circulante01, t2: Tiempo Circulante02
Las matrices circulantes son ejemplos de matrices toeplitz. Las matrices de Toeplitz surgen en muchas aplicaciones y son constantes a lo largo de sus diagonales. Por ejemplo,
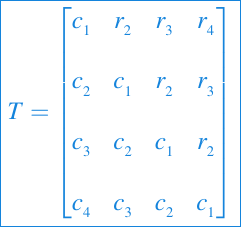
Si
c y r son vectores de dimensión n, entonces T = toeplitz(c,r) configura la matriz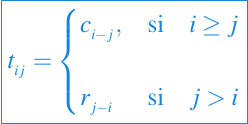

Muchas clases importantes de matrices tienen muchos ceros. Matrices triangulares inferiores
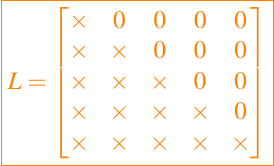
matrices triangulares superiores
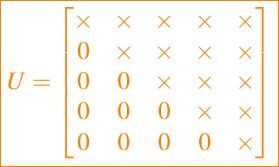
y matrices tridiagonales
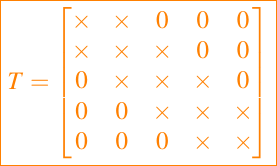
son los casos especiales más importantes.
En general, una matriz A = (aij) tiene un ancho de banda inferior si aij = 0 siempre que i > j + p. Así, una matriz triangular superior tiene un ancho de banda inferior de 0 y una matriz tridiagonal tiene un ancho de banda inferior de 1. Una matriz A = (aij) tiene un ancho de banda superior de aij = 0 siempre que j > i + q. Por lo tanto, una matriz triangular inferior tiene un ancho de banda superior de 0 y una matriz tridiagonal tiene un ancho de banda inferior de 1. Aquí hay una matriz con ancho de banda superior 2 y ancho de banda inferior 3:
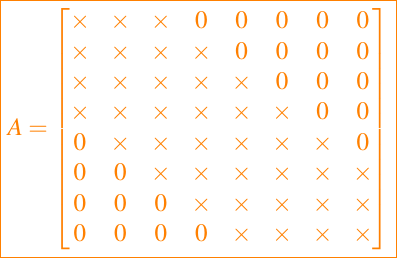
Las matrices diagonales tienen un ancho de banda superior e inferior cero y se pueden establecer utilizando la función
diag. Si d =[10 20 30 30 40] y D=diag(d), entonces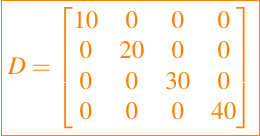
También son posibles las llamadas a la función
diag con dos argumentos, que pueden utilizarse para referirse a las otras diagonales de una matriz. Una entrada aij está en la diagonal késima si j - i = k. Para aclarar esto, aquí hay una matriz cuyas entradas son iguales a los valores diagonales: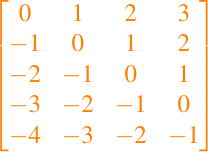
Si
v es un vector de dimensión n, entonces D = diag(v,k) establece una matriz de orden (m + k) por (m + k) que tiene una diagonal k-esima igual a v y es cero en todas partes. Por ejemplo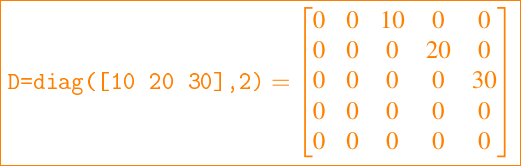
Si A es una matriz, entonces
v = diag(A,k) extrae la diagonal k-esima y la asigna (como un vector columna) a v. Las funciones tril y triu pueden ser usadas para perforar una porción de la bada de una matriz dada. Si B = tril(A,k), entonces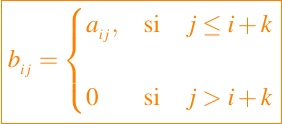
Análogamente, si
B = triu(A,k), entonces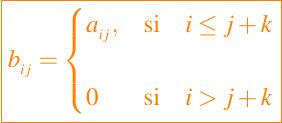
El comando
T = -triu(tril(ones(6,6),1),-1) + 3*eye(6,6)configura la matriz
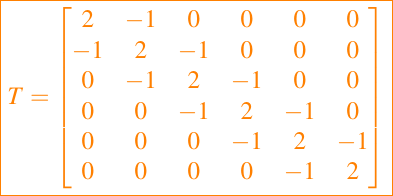
Los comandos
T = -diag(ones(5,l),-1) + diag(2*ones(6,1),0) - diag(ones(5,1),1)T = toeplitz([2; -1; zeros(4,1)], [2 ; -1; zeros(4,1)])hacen lo mismo.

La notación
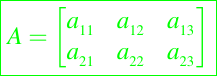
significa que A es una matriz de 2 por 3 con entradas aij. Se entiende que los aij son escalares, y Octave soporta la síntesis de matrices en este nivel (es decir,
A=[a11 a12 a13; a21 a22 a23]) La notación puede generalizarse para manejar el caso cuando las entradas especificadas son matrices mismas. Suponga que A11, A12, A13, A21, A22 y A23 tienen las siguientes formas: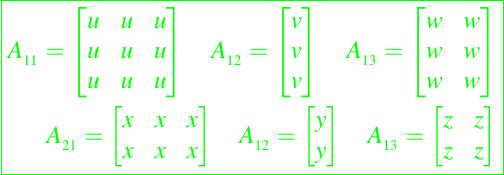
Luego definimos la matriz de bloques de 2 por 3 como

por

Las líneas delimitan las entradas de bloque. Por supuesto, A es también una matriz escalar de 5 por 6. Las manipulaciones de la matriz de bloques son muy importantes y se pueden llevar a cabo de forma efectiva en Octave.
El script siguiente:

Script para la construcción de una matriz por bloques. Elaborado en GNU Octave, por @abulmath.
resulta en la formación de la siguiente matriz

Las filas de bloques de una matriz están separadas por punto y coma, y es importante asegurarse de que las dimensiones sean consistentes. El resultado final debe ser rectangular a nivel escalar. Por ejemplo,
A = [1 zeros(1,6); zeros(2,1) [10 20;30 40] zeros(2,2); zeros(2,3) [50 60;70 80]]configura la matriz

La extracción de bloques requiere la notación de colon. La asignación
C = A(2:4,5:6) es equivalente a cualquiera de las siguientes:C = [A(2:4,5) A(2:4,6)]C = [A(2,5:6) ; A(3,5:6) ; A(4,5:6)]C = [A(2,5) A(2,6) ; A(3,5) A(3,6) ; A(4,5) A(4,6)]Queridos amigos y lectores, espero hayan disfrutado de esta segunda entrega de este tan apasionante e interesante tema del cálculo numérico, Cálculo Matricial | 1era Parte apoyado con el entorno GNU Octave, en esta oportunidad pudimos estudiar algunas características y formas de las matrices y como optimizar su almacenaje. Espero que el mismo sea de apoyo a ustedes en sus trabajos, o quizás sirva de apoyo para sus hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Hoffman, K., and Kunze, R. Álgebra lineal. Prentice-Hall Hispanoamericana. 1973.
- Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
- Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
- Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.
La imagen de fondo de la portada es una imagen de libre uso tomada de 
 , GIMP e Inkscape.
, GIMP e Inkscape.
@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.







¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Entra aquí para más información sobre nuestro trail.Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias por la valoración y consideración a mi trabajo. Saludos cordiales.
¡Increíble genio de la matemática! Excelentes explicaciones, creo que eres único en la comunidad hispanohablante con semejante capacidad para profundizar de manera didáctica en esta área. Mis respetos.
Es una frase que me deja sin palabras, una valoración muy grande. Seguramente, hay otros por allí escondidos detrás del escenario, y yo me estoy llevando los créditos por ahora. Agradecido por tus halagos. Las razones que me llevan a escribir sobre matemáticas es mi amor y pasión por tan bella ciencias. Quizás muchos no los entiendan, pero la verdad es que cuando los escribo me inspiro tanto que me excedo un poco.
Una de más grandes motivaciones es dejar plasmado en la blockchain un poco de mi sello personal al redactar y escribir mis publicaciones. Espero que muchos puedan aprender con los temas que publico. Pero reconozco que puedo hacerlos un poco más digeribles para todos. Pronto vendrán sorpresas gratas en mi Blog, y espero que les guste ese nuevo estilo.
Saludos y un fuerte y caluroso abrazo.

Hola @ivymalifred, guaoooDefinitivamente las matemáticas no son mi fuerte..lo haces muy bien!
Hola Dra. @alexaivytorres, gracias por tu valoración, cada día tratando de hacerlo mejor y poder ser tan destacado como usted en todos sus trabajos. No soy un experto en Biología, pero sus publicaciones son excelentes, y motivan a leerlas.
Le envío un abrazo fuerte. Saludos Cordiales.
Saludos @abdulmath, me gusta la diagramación de tu post y las imágenes que en el presentas, interesante tema del mundo de las matemáticas.
Hola @pinedaocl, gracias por visitarme en el blog, y tomarte un tiempo en leer esta publicación. Un trabajo y esfuerzo por tratar de ser mejor bloguero. Saludos y un abrazo.
Excelente trabajo amigo, me gusta su perspectiva... siga asi. saludos.
Hola @chiki, gracias por leer mi blog. Que bueno te guste. Gracias y saludos
La matemáticas son interesantes, nunca han sido mi fuerte pase mucho trabajo mientras estudiaba, pero admiro a las personas que les gusta las matemáticas. Saludos
Hola @evero, muchas gracias por tu visita. Si la Matemática es mi pasión.
Saludos y un fuerte abrazo.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.