Hello and best regards for everyone my friends of steemit. Learning math could be a very hard task because the complexity of this subject, and many students ask: Does exist any key to learning math?, and the answer is: yes, that key (or keys) does exist, but they anen't magic keys, I mean, You won't learn math from the night to the day, the first key is to be constant.
When I'm starting any course of math, I allways speak about myself when I was an student at high school, I was stunned in math, Iwas very bad student in math, even when I started at university, having a best knowledge in math, again I have problems to understand calculus and my suffering started again. However nowadays I'm teaching maths at both levels: high school and universitary, and I have this question to my students: how do you think i could learn math? So in this post I'm going to explain the keys that I use to achieve my learning of mathematics.
First key: BE CONSTANT: the other keys are useless if you are not constant, maths are difficult? yes they are but it's not impossible to learn it, so don't surrender at the first difficult remember the first key.
Second key: THE RULES: it doesn't matter if we are talking about math of high school or calculus, all mathematics are constructed over rules, this rules are expressed in simple terms so to understand it should not be difficult, maybe in calculus where the mathematical language can be confusing, there I recommend doing a kind of translation (Yes, a traslation), so once You learn the rule in the simple terms You must be able to adapt it to a complex form. Let's see a couple of examples:
1.- The algebraic sum: when we start the high school we learn that the sum and the rest (two of the four basic mathematics operations) are not separated any more (because the distiction between the positive and negative numbers or integer numbers), now they are together in one operation that we know as algebraic sum and this operation has two rules to aply in a calculatión, thar rules are:
1.1) If the numbers has the same sign (I mean, both are positives or both are negatives) You must sum (normal sum) the numbers and kept the common sign, in other words, if You have the following numbers: -2-9 its algebraic sum will be -11 or if we have the numbers 5+7 its algebraic sum will be 12 (or +12).
1.2) If the numbers have different signs (one positive and other negative) You must rest (normal rest) and the result will have the sign of the number with greater absolute value. So if we have the numbers: -4+7 the algebraic sum will be +3 and, on the other hand if we have: -8+2 the algebraic sum will be -6. Here we have the rules of algebraic sum exposed in the simple way.
Now, how we can proceed (based on rules of the algebraic sum) if we have the following operation: -5+8-6+3-1+2?
If You understood the rules, easily You can see that the 1.1) rule can be applied on those numbers having the same sign, so we'll have: -5+8-6+3-1+2 = -12+13, notice that the number -12 is obtained adding up the negative numbers in the operation, and at the same way we can do for the positive numbers to obtain the result +13. Now we reduced a large sum in the algebraic sum to only two numbers, there we can apply the 1.2) rule: -5+8-6+3-1+2 = -12+13 = 1, and we can write all in the following form: -5+8-6+3-1+2 = 1. So You can see how You can solve a complex operation using the rules in it's simple form.
2.- The other example that I want show is a little bit complex because we won't use numbers, we'll use letters instead, we use algebra. In other post I explained the notable product that we can write in it's simple form as:

In order to learn this formula we can recite it as follows: the square of the first term (a^2) plus the double product of the first term by de second (2ab) plus the square of the second term. in this way many students learns the notable product in it's simple form, now we'll use this knowlede of the formula to apply it in the next operation:
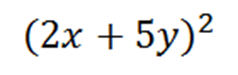
As You can see, the terms are no simple as the terms in the formula, here the important point is to know wich is the first and the second term and use our translation of the formula like this
The square of the first term: 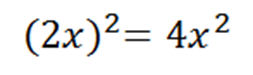
The parenthesis is used to indicate that all (the number 2 and the letter x) are squared. We continue
The double product of the first term by de second: 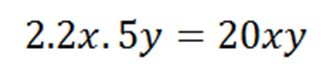
In this part we have multiplied the numbers 2x2x5 = 20 and the multiplication of 20 and the letters we left indicated as 20xy.
The square of the second term: 
Is done the same as in the part of the square of the first term.
Now, putting all together we we'll have the following result:
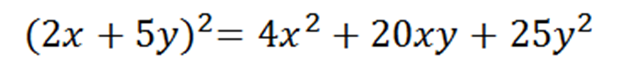
You can see that we strictly follow the rule to obtain the notable product requested, also You can see that follow the rule in it's simple form is very easy.
With this two examples is well explined the second key, we can pass to the third key.
Third key: TO PRACTICE: Let me ask a question in this part: why Michael Jordan, Lionel Messi, Miguel Cabrera, Michael Scumacher, Usain Bolt and others big athletes are (or were) the best in their sports? There is not only a matter of talent, they also PRACTICE a lot in order to become in the icons they are. In math is the same, practice makes a master so, when You learn one rule You MUST practice and practice and practice until You reach to dominate the application of that rule in simple and complex operations and in this part is where yo MUST be constant also.
So, I follow this keys and the result is that now I'm teaching math, therefore, if I could become into a master of the mathematics being that in my beginnings I was not good, You can do also, when my students understands this keys they starts to see light in maths.
I hope this post can be useful for people who really wants to learn this important subject in their education because math is in everything and is useful in any universitary career You want to study.
If You like this post and want to have an adaptation to advance math (calculus) please let me know in the comments and and i will gladly do it.
Reference of the image:
Hello, good post brother.