The Calculus of Hot Chocolate Pouring!

Who doesn't love a cup of hot chocolate on a cold winter's night in front of a glowing fire? What could be more instantly gratifying than pressing a button on the Barista machine and watching that cup fill up with all of that goodness?

Image Source

Suppose a paper cup manufacturer wants to put its product to the test and determine if the dimensions of its cup are just right. For whatever reason, they would like to know if there's an equation that could tell them exactly the level of a liquid that is being poured into their cup at anytime (from the start of pouring).

They manufacture cups in the shape of a truncated cone (called a "frustum") as shown in Figure 1.

Figure 1.

A barista machine dispenses hot chocolate at a constant rate, such that the increase in the volume of the liquid in the cup over time is constant. That is...

Now, if the cup was cylindrical, or any uniform shape, the volume can generally be expressed as Area of its base by the height...

Unfortunately, our hot chocolate cup is not a cylinder. It is tapered, and as such, the cross-sectional area of the liquid contained in it changes with height h. Which, to use a cliche, puts a bit of a spanner in the works.

Let's take small cross-sectional slices of the liquid volume of a very small height 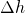, such that the volume is divided into many thin disks 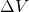, as shown in Figure 2.

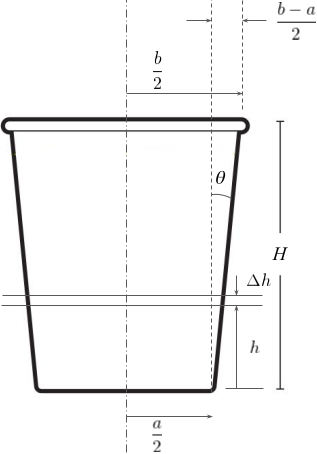
Figure 2.

As these disks are so thin, the taper has a negligible effect on their volume, which can be expressed as...

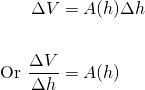
Then taking the limit as 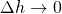, we have the derivative (or rate of change) of the cup volume with respect to height as...

Now, the area of the cross-section at any height is a circle, and can be expressed as...

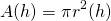
... as the radius of the circle depends on h. From Figure 2, we can use a little trigonometry to work out .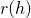

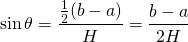
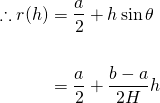
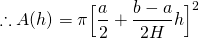
Substituting the expression for in to (1), we have...

Ok, so we know that the volume increases in the cup at a constant rate K, and we also know that the volume also depends on the height of the liquid. So by the chain-rule...

And thus substituting (2), the expression for dV/dh, we have...

Now equation (3) is a separable, first-order, non-linear ODE...

Integrating both sides...

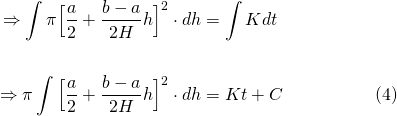
We can use the method of u-substitution to evaluate the integral on the right-hand side...

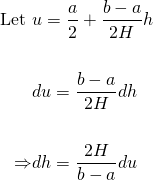
...and so the integral becomes...

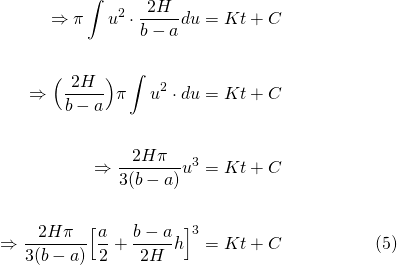
Now rearranging (5) to solve for h...

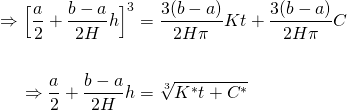
where...

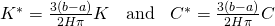
since 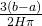, K and C are constants, then 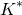and 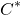are also constants. So, continuing on...

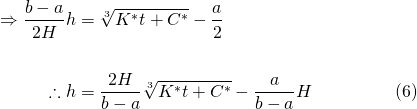
Equation (6) is the general solution. We can find the particular solution by applying the initial values. At the start of the pour, when t = 0, the liquid level in the cup h = 0...

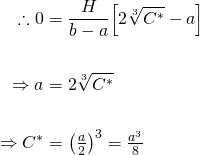
And finally, we have...

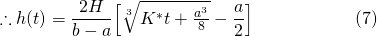
Now, here's a selection of cup sizes from this manufacturer...

Image Source

Let's test our solution on the "340mL" cup, which has the following parameters...

• height H = 97mm
• a = 59mm
• b = 89mm

Suppose that the machine we are using pours hot chocolate at a rate of dV/dt = 30mL /s = 30 000mm³/s, we can find the value for ...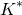

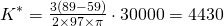
Substituting all of the other numerical values into equation (7), we have...

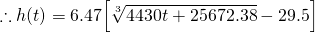
A plot of this relationship between h and t is shown in Figure 3. As you can see, the increase in height of the liquid gradually slows down with time as the cup is filled. This would be straight line relationship if the cup was a cylinder.

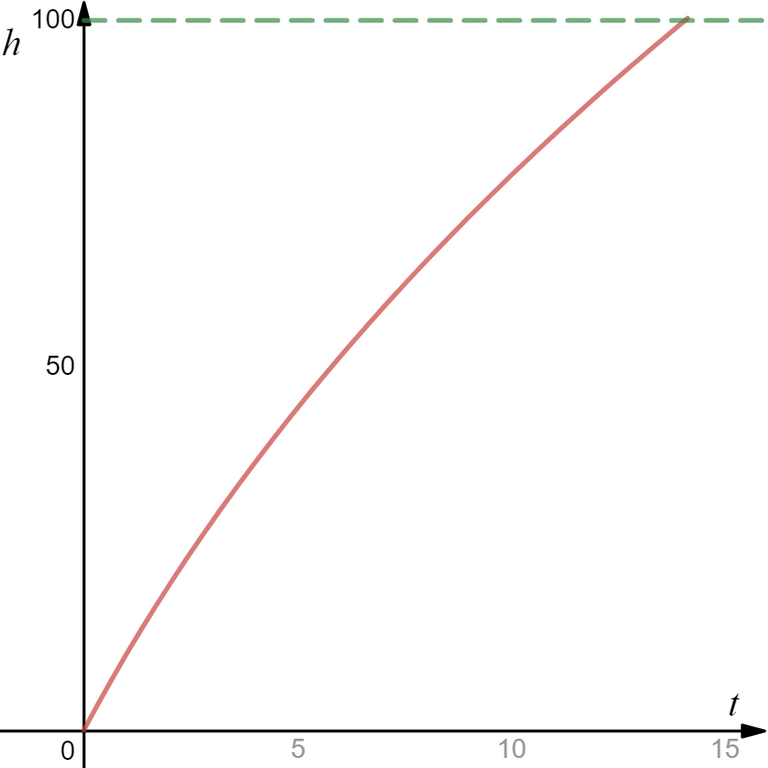
Figure 3.

Now exactly how long does it take to fill the cup to the brim, given its height of 97mm?

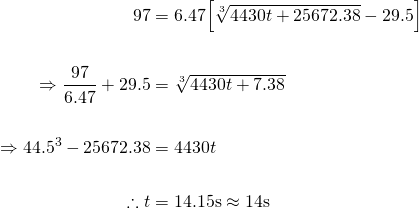
So it takes about 14s to fill the cup, which sounds very reasonable. How do we know this result is accurate?

Well, the manufacturer claims this cup has a volume of 340mL, which if we're pouring at 30mL/s, should only take just over 11s. If we check the volume of the cup against the formula for calculating the volume of a frustum...

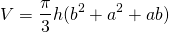
...it turns out the volume of this "340mL" cup is actually about 423mL (they may have specified 340mL to prevent people from over pouring into the cup), which does indeed require 14s to fill at a rate 30mL/s.

---

Credits:

All equations in this tutorial were created with QuickLatex

All graphs were created with www.desmos.com/calculator

---

Below is a list of tutorials I've created so far on the subject of First Order Differential Equations:

1. Introduction to Differential Equations - Part 1

2. Differential Equations: Order and Linearity

3. First-Order Differential Equations with Separable Variables - Example 1

4. Separable Differential Equations - Example 2

5. Modelling Exponential Growth of Bacteria with dy/dx = ky

6. Modelling the Decay of Nuclear Medicine with dy/dx = -ky

7. Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky

8. Mixing Salt & Water with Separable Differential Equations

9. How Newton's Law of Cooling cools your Champagne

10. The Logistic Model for Population Growth

11. Predicting World Population Growth with the Logistic Model - Part 1

12. Predicting World Population Growth with the Logistic Model - Part 2

13. There's a hole in my bucket! Let's turn it into a cool Math problem!
14. The Calculus of Hot Chocolate Pouring!

---

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3

Tip me at PayPal: https://paypal.me/MasterWu