Hello everyone! Good day to all of you! :)

I am @renz1995. My real name is Jay Peterson Indoc. My nickname is quite far related to my real name since I got my nickname " Renz " from my friends only. They called me that way because there was "Renz" in our place who's quite similar to me, that's what they said, hehehe.. I am a new Steemian from Philippines. I heard that this website gives opportunities to everyone not just to learn but also to earn. It caught my interest so that's I will be joining the team :)

Today, I am going to start giving tutorials on Mathematics. This tutorials that I will be teaching is not an ordinary tutorial. I will not be solving the problems the usual way on how you solve a given Mathematics Problems. Hmmm... Let's just say that I am having a Review Program here on Steemit. So now let's start and let's get it on :)

What is Analytic Geometry?

According to Wikipedia - Analytic Geometry

In classical mathematics, analytic geometry, also known as coordinate geometry, or in a common manifestation Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

Analytic geometry is widely used in physics and engineering, and also in aviation, rocketry, space science, and spaceflight. It is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.

Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.

---

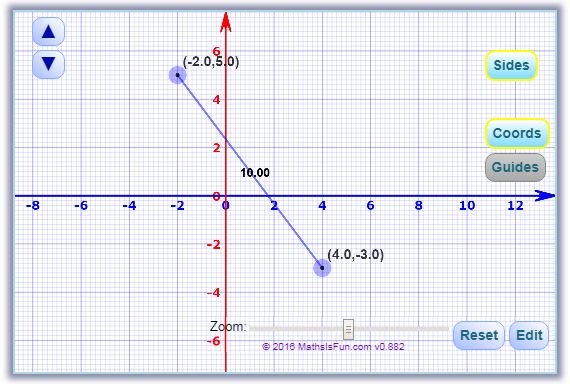
Number 1. Find the distance between A( 4, -3 ) and B( -2, 5 ).

Given:

• Point 1 at A( 4, -3 )
• Point 2 at B( -2, 5 )

Required:

• Distance between Two Points

Solution:

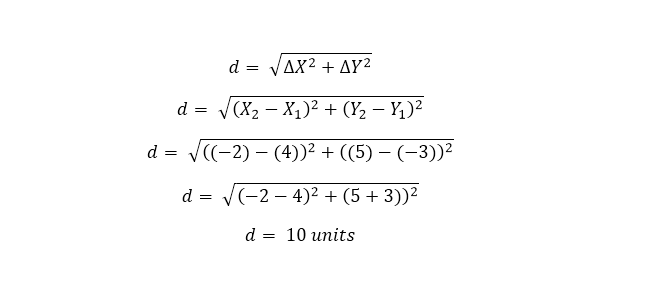
Graph Representation Made From MathIsFun - Online Graph Maker

---

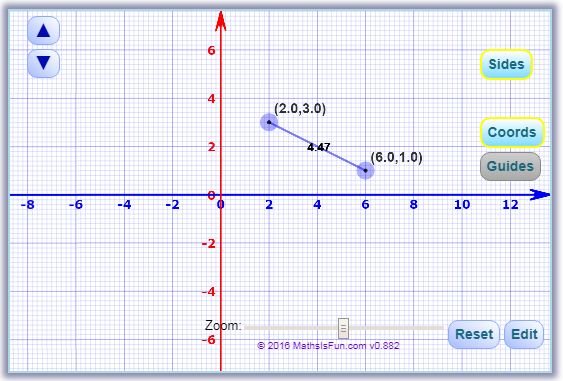
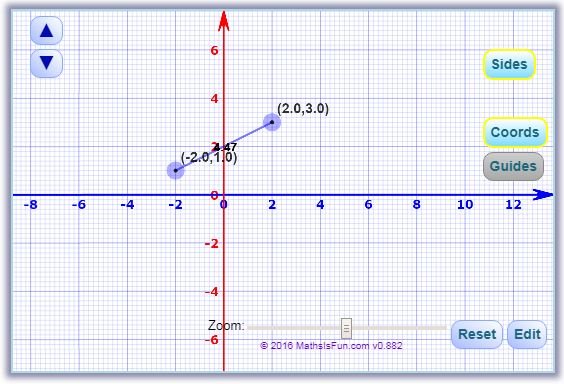
Number 2. The point ( x, 1 ) is 2 square root of 5 units from ( 2, 3 ). Find the value of x.

Given:

• Point 1 at ( x, 1 )
• Point 2 at ( 2, 3 )
• Distance Between Two Points = 2 square root of 5 units

Required:

• The Value of x

Solution:

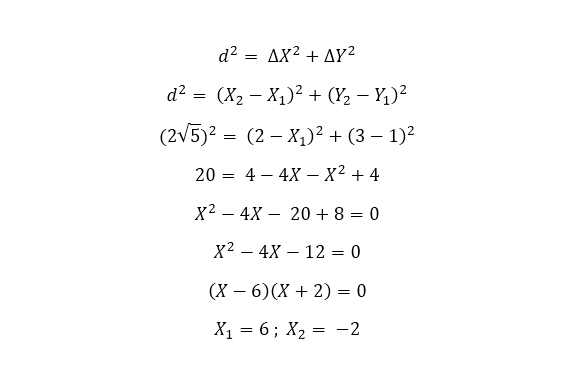
Graph Representation Made From MathIsFun - Online Graph Maker

OR

Thank You For Reading! I hope you've learned something ^_^

Author: @renz1995