Quiero compartir con Uds. mis apuntes de Física. En este post, me referiré a dos conceptos básicos en física general cuyas definiciones tienden a confundirse: centro de masa y centro de gravedad. Esto es porque en los cursos de física básica (Bachillerato) y física I (Pre-grado), solamente trabajamos con objetos isotrópicos en campos gravitatorios homogéneos, y generalmente no se explica la diferencia ni en qué casos no coinciden.
En un próximo steem, les presentaré algunos experimentos caseros...

Experimento típico para estudiar el centro de masa y gravedad
(@jfermin70: foto propia, apuntes de Física 1, LUZ)
Centro de masa
El centro de masa (CM) se define como la región del espacio donde se concentra la masa de un objeto, depende de la distribución de masa y la geometría del objeto. En un sistema discreto, como el de la Figura 1, el centro de masa se localiza a lo largo del segmento que pasa por el centro de ambos cuerpos, de acuerdo la ecuación,
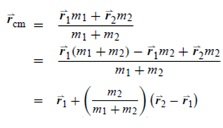

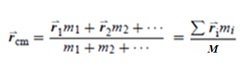
donde M es la masa total del sistema. El lugar geométrico donde se localiza el CM a veces también se denomina centroide.
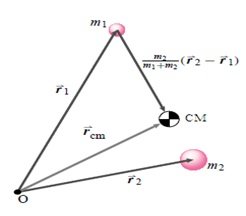
Figura 1. Sistema de dos masas, indicando el centro de masas (ruina.tam.cornell.edu/Book/COMRuinaPratap.pdf)
En cuerpos continuos, la posición del CM se determina mediante el cálculo de la integral,
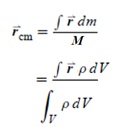

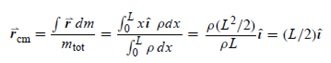

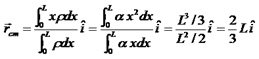
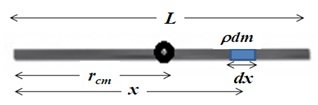
Figura 2. Esquema para calcular la posición del CM de una varilla de densidad lineal uniforme. El CM se localiza en el punto medio de la varilla (@jfermin70: apuntes de Física 1, LUZ)
El CM se desplaza hacia la derecha del centro de la varilla. Este simple ejercicio ilustra la importancia del CM en problemas ingeniería, ya que efectos térmicos y/o cargas externas pueden desplazar el CM y afectar estructuras civiles, mecánicas, etc. Además de esto, muchas propiedades dinámicas pueden simplificarse mediante el cálculo del CM.

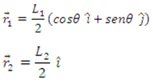
y consecuentemente, la posición del CM viene dada por,
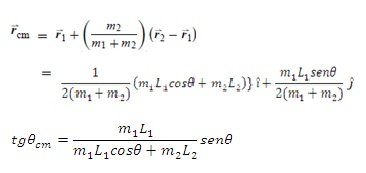
En el caso de dos varillas idénticas, obtenemos que la posición del CM está determinada por las relaciones,
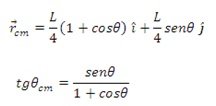
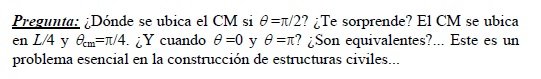
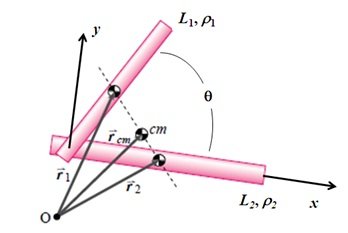
Figura 3. Geometría generalizada para calcular la posición del CM de dos varilla de densidad lineal uniforme. El cálculo se simplifica considerando un eje horizontal a lo largo de la varilla “2”.
(Adaptación de la Figura original: ruina.tam.cornell.edu/Book/COMRuinaPratap.pdf)
Centro de gravedad
El centro de gravedad (CG) es el punto en el cual la resultante de las fuerzas de gravedad aplicadas sobre cada porción del objeto físico. Si el material es homogéneo, la fuerza aplicada en cada punto es la misma. El CG no necesariamente se encuentra dentro del objeto, es decir la fuerza resultante puede estar aplicada fuera del cuerpo material, tal como en los objetos mostrados en la Figura 4.

Figura 4. Objetos en los cuales el CG no coincide con los puntos materiales del cuerpo: a) semi-esfera hueca; b) objeto curvo; c) toroide. (@jfermin70: foto propia, apuntes de Física 1, LUZ)
Para calcular posición del CG de un sistema de discreto, debemos considerar el torque neto producido por la fuerza de gravedad actuando sobre cada una de las masas que conforman el sistema, tal y como se muestra en la Figura 5. El torque aplicado en el CG es perpendicular a la superficie del papel y determinado por la ecuación,
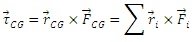
Si la única fuerza que actúa sobre el sistema es el peso de cada partícula, entonces el torque es,
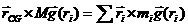
En la geometría de la Figura 5 el peso está aplicado a lo largo de la horizontal. Luego de realizar el álgebra vectorial, y comparar términos, obtenemos que la posición del CG está determinada por las coordenadas,
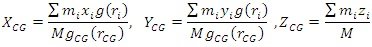
El CG no coincide con el CM si el campo gravitatorio depende del punto de aplicación de la fuerza. Si el campo gravitatorio es homogéneo, g(ri ) = g(rcg) = g, se cumple que,
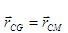
¡El centro de gravedad y de masa coinciden!
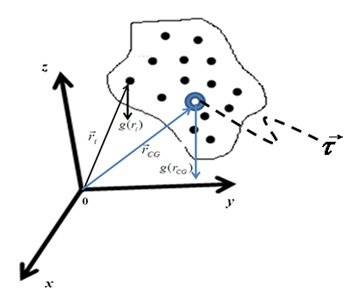
Figura 5. Geometría utilizada para el cálculo de la posición del centro de gravedad de un sistema de discreto de masas (@jfermin70: apuntes de la cátedra de Física 1, LUZ)
Sumario
En resumen, he mostrado que en general, el centro de masa y el centro de gravedad son diferentes, y solo coinciden en el caso especial de cuerpos isotrópicos en un campo gravitatorio homogéneo. Todas las cantidades físicas de un sistema discreto o continuo, se pueden representar en un sistema de referencia que contenga al centro de masa o de gravedad.
Finalmente, determinar la localización precisa de ambos CM y CG es esencial para la estabilidad de estructuras tanto civiles como mecánicas.
Libros recomendados (Nivel universitario)
Hugh Young, Roger Freedman, FÍSICA UNIVERSITARIA, V.1, Addison Wesley, 12da Edición, México (2009)
Frederick Bueche, Eugene Hecht, FÍSICA GENERAL, Serie Schaum, Décima Edición, McGraw-Hill, México (2007)
Herbert Goldstein, MECÁNICA CLÁSICA, Editorial Reverté, Traducción de la 2da edición, España (2006)
S. T. Thornton and J. B. Marion, CLASSICAL DYNAMICS OF PARTICLES AND SYSTEMS, 5th ed., Brooks/Cole, Belmont (2004)
Siendo un SteemStem Estados
Muy buena información. Saludos
Gracias Daniela, espero estés bien...
Muy buen trabajo mi estimado amigo. Te deseo muchos éxitos. Saludos
Muy buen post amigo y colega @jfermin70. Poco a poco se irá mejorando el formato. Lo felicito.
¡Votado!
Saludos. 😁
Excelente trabajo @jfermin70, ciertamente un concepto que muchos confunden. Éxito en sus artículos.
Maravilloso post @jfermin70 es muy importante tener con nosotros personas con excelentes conocimientos científicos. Solo un pequeño detalle nuestra etiqueta se escribe con #stem-espanol.
Saludos!!
OK, ya lo modifiqué. Gracias...