A while back I did some experiments with protein in my diet versus my bodies protein mass as measured by the top of the line BIA scale they have at my gym. Now recently I did an other, much shorter experiment. In this blog post I want to discuss the different types of experiments you can do that use engineering to make N=1 experiment as valuable, at least for the one involved (you), as any N=100,000 could ever be. I want to put it against larger N equals many experiments and discuss the limitations of both.
Control feedback theory for N=1
Most of the time I try to use an engineering setup to my experiments that is very different from the statistics based approach that scientists use to draw conclusions. The way that this approach works is that, making some assumptions about the shape of the true relationship between two variables, and making some assumptions about the latency in the bodies own feedback loops, you can design a feedback loop with the objective of finding the local maximum or local minimum in the relation between X and Y. No guarantee there isn't an even lower minimum or higher maximum somewhere else on the X->Y graph, so if I start my protein intake at 150 grams per day and find a local maximum for my target variable at 220 grams of protein, there might very well be an even higher maximum at 400 grams or at 100 grams, but, as finding a single local maximum takes months and there is a huge set of other variable sets that may be of interest, I'll settle for the one local maximum and assume it to be the maximum.
Some target variables are noisy. That noise could stem from other poorly controlled input variable, for inconsistencies in measuring regime, or they could stem from our black-box (our body) itself. In the later case, there is an interesting little trick in control feedback theory helping us to overcome internal noise. By modulating the input with something approaching an harmonic signal and using a combination of a negative feedback loop and a band filter, it becomes possible to find a local maximum or local minimum while despite of internal noise sources. Practical issue with this though, where low noise output variable will take months to find a local minimum or maximum for the input variable, doing so with a noisy output and a modulated input will considerably stretch this. Given that this is N=1 engineering and with there being zero exact duplicates of me, this creates a practical problem of time availability. So rather than doing a single N=1 experiment that takes maybe a full decade to complete, we take a shortcut. We sample the transference. Here the validity of our single maximum (or minimum, depending on what we are aiming for) assumption becomes important, because, if that assumption is valid, we can do a binary search for our local maximum.
What you do to accomplish this is you pick a point on the X axis, modulate your input signal around that X, use the output in your feedback code, than measure the amplitude and phase of the output signal compared to the input.
Let's say we are looking for a local maximum. If our chosen X is below our maximum, than the output Y signal should lag minimally behind on the signal X. If we are past the local maximum with our chosen X, then the phase of the output signal should be at or slightly above 180° when compared to that of the input signal.
Small N=1 experiments based on strong predictions.
When doing experiments for your own personal N=1, there is an other option, other than control feedback based experiments. An option with the potential of finding modest answers to much stronger predictions. While these experiments could provide valuable information it is important to note that the information it could give is nowhere close to the strength implied by the hypothesis needed to start the experiment. Let me try to explain using the two experiments I ran recently, of of them still ongoing (even though it failed to confirm the hypothesis).
Some context: Protein 3x/day
Using control feedback experiments as described above, I found, looking for a local maximum for both strength using runs for LBM, BF% and strength stats and (BIA) body protein mass that :
- My local maximum starts around 200 grams a day for LBM and strength purposes and at 240 for BF% purposes after that, it basically flat-lines.
- When at unchanged caloric intake, using modulated CF for experiments, output signal is indistinguishable from from probabilistic noise between 240 grams and 375 grams.
- Below 120 grams per day, drop in LBM becomes too dramatic to run experiments long enough to be useful.
- Above 380 grams per day, decrease in appetite make eating up to caloric targets to uncomfortable for running experiments long enough to be useful.
Is 3x/day protein is very important
Now for the short experiments. So far, all my protein experiments were based on three meals a day. Data from people doing Intermittent Fasting however were making me quite interested in looking into it for myself, but worries about protein intake kept me from trying anything like that. Than one person put an interesting thought in my mind, the thought that somehow, meat would be slow release protein. While I could find nothing in literature to confirm the validity of this theory, the idea of trying out what people refer to as "Zero Carb" was also on my list of things to explore.
As my experiences with Keto had shown me that reducing carbs has a huge influence on Inter Cellular Water levels, total Lean Body Mass (LBM) figures would be of little use. Yet body protein mass should prove potentially useful. Problem though, protein mass is a relative small portion of the Lean Body Mass and the granularity of the BIA scale for protein mass is only 0.1 kg. So if I wanted to do an experiment to test a hypothesis on IF and protein, I had to do it in a way that would result in a regression line that would imply a protein mass loss of at least 300 grams.
So in order to make a hypothesis about IF and protein, the consequence of this hypothesis would need to be an effect of at least 300 grams of body protein mass loss. To do this, I used the following hypothesis:
- A single meal with approximately 375 grams followed by 36 hours of fasting equates 12 hours of adequate protein followed by 24 hours of severely inadequate protein.
Applying my experience with (abandoned) < 100 gram of protein runs, this hypothesis would have me lose over 400 grams of protein mass in just six 36 hour cycles. A number well beyond the probabilistic noise level for BIA protein mass measurements. At least, so I thought.
So for the outcomes. Well, let me start of by saying my hypothesis didn't pan out. While I did lose some protein mass in my 9 day experiment, the loss was no way as dramatic as predicted by my hypothesis. In fact, it was higher than the 0.1 kg granularity of the BIA measurements, but small enough to only be effectively measurable using a regression line. Needless to say the measured value from such a regression line between low granularity measurements is rather unreliable, but the important thing, it was low enough to falsify my hypothesis of a strong negative effect on protein mass from Intermittent Fasting combined with high protein meals.
An unexpected pattern
The first unexpected piece of information about my 9 day experiment was the amount of difference between measurements within a single 36 hours time frame. In retrospect it makes sense that taking meals containing almost 400 grams of protein once every 36 hours would cause fluctuations, but in advance I didn't consider that given the low fluctuation rates I had in earlier experiments eating protein three times a day. So this part isn't all that interesting. The thing that was interesting though was the first (or the last, depending of how you look at it) of every cycle.
I was taking BIA measurements at the gym, twice a day. The first one after my meal, than a second and third one 12 and 24 hours later. Looking at the delta's between measurements, the delta between the first and the second and the delta between the second and the third measurement always seemed to follow the same pattern. The delta between the third of one cycle and the first of the next, however were where it became interesting. That is, looking at the delta's it becomes a viable hypothesis to attribute all of the protein mass loss to the third 12 hours of of the even cycles. That is, in the cycles starting with a diner, the last night of sleep may be responsible for all of the protein loss within a larger 3 day cycle. So I'm currently setting out to test this new idea.
Coin flip experiments
So here it gets interesting. My observations from my 9 day experiment were interesting in the sense that they could be brought back to the idea of a coin flip. If the delta after the meal is lower than a certain threshold, we equate it to a heads, if its higher we equate it to tails. There was an easy to find threshold in my first experiment. All three of my after breakfast measurement delta's were below that threshold, all three of my after diner delta's were above that threshold. Now, lets assume this was by pure chance, that this was like a simple coin flip. That would mean the probability of repeating this experiment and getting the same outcome would be one in sixty four. Note that we absolutely need to do an other experiment as you should never use the data set that allowed you to create an hypothesis to try and prove that hypothesis!.
Repeating the same experiment however would assume zero probabilistic noise, it assumes that a weighted coin would always only land on heads, so to speak, an assumption we probably shouldn't make. So where we would need six full cycles panning out 100% to make our assumption viable that this observed pattern is real, we can add some power to our experiment by making the experiment a bit longer. Remember, we are looking at the experiment as a set of coin flips where we want to test if our coins are biased, but the only way we can ever show they are biased at all, we need to observe results in line with being severely biased. See, its a short running experiment using N=1 and we are not doing control feedback. It isn't possible to show the size of an effect using only a few data points without using some kind of modulated control feedback, something that is impossible with binary input such as breakfast vs dinner, if the effect size is large enough, not necessarily 100% but close, then we can show that there very likely is an effect there.
If possible it is wisest to use sampling modulated control feedback runs to base experiments, but for binary inputs that can not be harmonically modulated, or for experiments that are potentially too risky to run for too long, coin flip type experiments can add greatly to our engineering
Poisson processes
It is a small step to go from coin flips to Poisson processes. For experiments using Poisson, we need to run two experiments with greatly differing expected results. If we look at my protein experiments, you could imagine running the experiment twice, or splitting it up in odd and even cycles and arranging the data as if it were two separate time series.
The important bit remains we need a really strong difference between the two experimental setups as with respect to the arrival frequency of one of our two outcomes if we want outcomes that are unlikely t o be spurious from a purely probabilistic point of view. What we'll be looking for is the results of a p value test for two Poisson arrival processes stemming from Poisson processes that in fact have the exact same lambda. I won't get into the mathematics of this test, as it will likely only distract from understanding, but if you never before used R-Studio, and if you never ever end up using it for anything else, I would suggest anyone doing N=1 experiments to at least check out the p value test for two potentially same lambda Poisson processes to play around a bit with expected outcomes so you can come to a proper length for your experiment design.
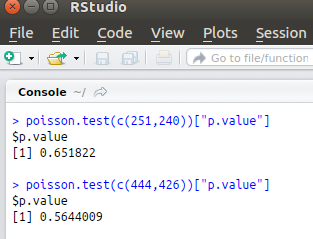
You give the test two numbers, namely the number of true outcomes for experiment number one and the number of true events for your binary outcome runs. These events could be "protein delta above threshold" or as we will see in the next section, in clinical trials they could be a patient dying. It doesn't really matter actually, and when people tell you N=1 experiments are worthless, I'll claim that they probably both have neither heard about Black's work on negative feedback loops and have a very poor grasp of the subject of Poisson arrival processes. Poisson equality p-test based N=1 experiments are exactly as good, from a statistics point of view as clinical trials using Poisson equality p tests when the number of events are the same and the proper variables are controlled for. One could even argue that it is easyer to control for variables and you are less likely to suffer from unforeseen confounders exactly when you are doing N=1 experiments. But I'l leave that discussion to the more philosophically inclined. While I love epistemological discussions, I'm an engineer and in this blog, I'm probably in the process of pissing off a lot of health professionals by challenging them with respect to their perception of N=1 experiments, so I'll better stick to what I know and not make any kind of possibly wrong philosophical statements about epistemological aspects of it all. What I however do dare to claim is that from a data perspective, equal sets of Poisson arrival numbers are equal in terms of weight of the evidence. It is irrelevant from a data engineering perspective if a set is the result of a huge N equates many trial or from a one person experiment.
Conclusions
While N=1 experiments are often frowned upon, and when done naively will yield poor evidence at best, there are techniques both from engineering and from statistics that allow N=1 experiments to provide quality evidence at least as strong and reliable as any huge N clinical trial could. Black and Poisson can and should be any N=1 experimenters best friends and, especially Black provides us with control feedback tooling that allows us to unearth information that would take many many clinical trials to find if it would even be possible. There is however one caveat. A local maximum or local minimum for one person might not be close to valid for the next. Ideally clinical trials could be designed to use Black in some sort of parallel way, and a best of both worlds could be achieved. There are advantages to using modulated input control feedback based experiments over Poisson based binary output, arbitrary threshold experiments, as Madame Poisson is an enigma that won't give up her secrets that quickly. I'll try to write a new post on some of challenges in getting useful evidence from Poisson arrival processes soon. Zooming in on some of the conclusions people seem to think we can draw from small observed effect versus large observed effect Poisson arival process event counts.
Did you bother checking ketogenic diet?
I have never seen you opine about it.
You got a 11.11% upvote from @ubot courtesy of @stimialiti! Send 0.05 Steem or SBD to @ubot for an upvote with link of post in memo.
Every post gets Resteemed (follow us to get your post more exposure)!
98% of earnings paid daily to delegators! Go to www.ubot.ws for details.
You got a 16.67% upvote from @luckyvotes courtesy of @stimialiti!
You got a 8.70% upvote from @sleeplesswhale courtesy of @stimialiti!
You got a 36.36% upvote from @proffit courtesy of @stimialiti!
Send at least 0.01 SBD/STEEM to get upvote , Send 1 SBD/STEEM to get upvote + resteem
Congratulations @engineerdiet! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Brazil vs Belgium
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes