Cómo estás hoy? Sinceramente espero que todos ustedes estén bien. La vida es bastante buena en este momento, así que trato de aprovechar al máximo mi tiempo y ser productivo. Esto no significa que no estoy ocupado, ¡solo va a decir que me encanta estar ocupado! Raramente tengo tiempo libre, pero cuando lo hago, prefiero pasarlo con mis seres queridos mientras disfruto de la naturaleza. Sí, lo sabemos. Pero esa no es la razón por la que estoy cargando este blog. De hecho, estoy de nuevo en el negocio con otro blog de Ingeniería, así que ¡hagámoslo! No otra vez...
Como prometí en mis publicaciones anteriores, que puede encontrar fácilmente haciendo clic en los enlaces que he proporcionado a continuación, esta es la octava parte de esta serie Introducción a la Cartografía. Esta vez aprovecho la oportunidad para compartir información amplia e introductoria sobre las coordenadas planas, que es una de las dos categorías principales de coordenadas utilizadas por los cartógrafos. También profundizaremos en los diversos sistemas de grillas "cartesianos" (me extenderé sobre esto) que se utilizan principalmente en el diseño del mapa hoy en día, ¡así que mantente concentrado!
Sí, estas son todavía publicaciones introductorias. Nos divertiremos mientras aprendemos cosas básicas e introductorias sobre el arte y la ciencia de crear representaciones en 2D de nuestro mundo 3D con precisión. Prometo que haré todo lo posible para recompensar su atención con bromas probablemente fallidas. De nuevo. Funcionó en el pasado. Como siempre, hay una gran posibilidad de aprender una cosa o dos leyendo este blog, ¡así que estad atentos!
 FUENTE
Para poder definir la ubicación de cualquier punto dado con precisión, Engineers tuvo la idea de crear sistemas de coordenadas. Estos sistemas incluirían información con respecto a la topología, que básicamente se refiere a cualquier tipo de correlaciones geográficas que garanticen la definición precisa del centro del sistema y la orientación de los ejes, así como también información sobre el sistema métrico y las unidades de medida utilizadas. Hay dos categorías principales de sistemas de coordenadas que se utilizan hoy en día, el primero de los cuales es el más antiguo y se conoce como Sistema de Coordenadas Geográficas. Sin embargo, en este blog nos centraremos en la segunda categoría, que recibe el nombre de Sistema de coordenadas planas.
FUENTE
Para poder definir la ubicación de cualquier punto dado con precisión, Engineers tuvo la idea de crear sistemas de coordenadas. Estos sistemas incluirían información con respecto a la topología, que básicamente se refiere a cualquier tipo de correlaciones geográficas que garanticen la definición precisa del centro del sistema y la orientación de los ejes, así como también información sobre el sistema métrico y las unidades de medida utilizadas. Hay dos categorías principales de sistemas de coordenadas que se utilizan hoy en día, el primero de los cuales es el más antiguo y se conoce como Sistema de Coordenadas Geográficas. Sin embargo, en este blog nos centraremos en la segunda categoría, que recibe el nombre de Sistema de coordenadas planas.
El Sistema de coordenadas planas, que también se denomina sistema de coordenadas ortogonales o rectangulares, es un sistema bastante antiguo también, con respecto a, al menos, su forma básica que se ha utilizado durante siglos. Este es el tipo perfecto de sistema de coordenadas para la definición precisa y la medición precisa de la ubicación de entidades geográficas situadas en la superficie de una proyección plana de la Tierra. El Sistema de Coordenadas Planas en su forma moderna se deriva del Sistema de Coordenadas Cartesianas, lo que es justo dado las similitudes en los atributos geométricos y el enfoque del diseño del sistema en general. Compartamos algunas palabras sobre Coordenadas cartesianas, que es el sistema basado en el cual se logró la creación del Sistema plano de coordenadas.
Coordenadas cartesianas
El Sistema de coordenadas cartesianas es en realidad una estructura matemática que se compone principalmente de un punto de partida en el espacio tridimensional con una ubicación conocida, y una unidad de medida específica para las distancias en el sistema métrico utilizado en el diseño del sistema. Dos ejes (Ox, Oy) a lo largo del plano Oxy se crean de forma tal que se cruzan con el punto de partida conocido del sistema y se orientan verticalmente el uno hacia el otro. Los ejes Ox y Oy se dividen con frecuencia en unidades de medida más pequeñas que se muestran en la proyección de una manera que sirve para mejorar la capacidad del observador de extraer información métrica observando el mapa.
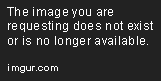 FUENTE
El mismo tipo de sistemas de referencia de análisis de distribución espacial se utilizan principalmente en el diseño y la construcción de representaciones gráficas. Por ejemplo, las revistas o los periódicos a menudo proporcionan gráficos estadísticos con respecto a varias encuestas, por lo que es seguro decir que en estos casos es totalmente decisión del observador absorber toda la información disponible y demostrada mediante el uso de esos elementos gráficos. Por supuesto, el autor, que en realidad es cartógrafo en nuestro caso, tiene la responsabilidad de hacer que la información esté disponible, sea fácil de comprender y obvia a la vista. El principal objetivo es un análisis de distribución espacial eficiente a través del diseño y la utilización del sistema de referencia apropiado; El Sistema de Coordenadas Cartesianas es lo que se necesitaba. El trabajo de los cartógrafos a nivel mundial depende de este sistema.
FUENTE
El mismo tipo de sistemas de referencia de análisis de distribución espacial se utilizan principalmente en el diseño y la construcción de representaciones gráficas. Por ejemplo, las revistas o los periódicos a menudo proporcionan gráficos estadísticos con respecto a varias encuestas, por lo que es seguro decir que en estos casos es totalmente decisión del observador absorber toda la información disponible y demostrada mediante el uso de esos elementos gráficos. Por supuesto, el autor, que en realidad es cartógrafo en nuestro caso, tiene la responsabilidad de hacer que la información esté disponible, sea fácil de comprender y obvia a la vista. El principal objetivo es un análisis de distribución espacial eficiente a través del diseño y la utilización del sistema de referencia apropiado; El Sistema de Coordenadas Cartesianas es lo que se necesitaba. El trabajo de los cartógrafos a nivel mundial depende de este sistema.
Los cartógrafos realmente usan el Sistema de coordenadas cartesianas como una guía y una base para establecer y definir los diversos sistemas de coordenadas utilizados en las asignaciones, a fin de lograr la simplificación de todos los cálculos necesarios para la conclusión de este proceso. Las diferencias en el proceso de cálculos entre la superficie de la proyección y la superficie de la esfera de referencia son triviales en casos de proyecciones conformes, sin embargo, los cartógrafos podrían necesitar utilizar diferentes sistemas de coordenadas de acuerdo con el nivel de precisión con respecto a los cálculos que se exigen. Vale la pena tener en cuenta que cuanto mayor sea el área de la Superficie Natural Terrestre que se representa en una proyección, menor será el nivel de precisión que se puede lograr. En otras palabras, es bastante significativo que los cartógrafos posean conocimientos avanzados sobre la magnitud de la precisión y la distorsión incluidas en las diversas proyecciones cartográficas que se utilizan principalmente hoy en día.
 FUENTE
FUENTE
Coordenadas planas
En una superficie de área hipotéticamente infinita, no se pueden detectar ni establecer ningún tipo de puntos de referencia sin la utilización de un sistema de coordenadas cartesianas. El punto de referencia necesario puede especificarse y anotarse como el punto en el que los ejes primarios del sistema se cruzan entre sí. Nuestro sistema se establece dividiendo el plano Oxy en cuadrados de igual área, lo que se logra con el grabado o equidistantes, líneas absolutamente paralelas que intersectan los ejes verticalmente. Después de haber logrado la creación de la cuadrícula del mapa como resultado del proceso descrito anteriormente, los cartógrafos ahora son capaces de definir las coordenadas de cualquier punto específico con precisión en relación con la ubicación dada del punto de referencia.
Para calcular los valores de coordenadas (X, Y), los ingenieros miden la distancia de cualquier punto específico de ambos ejes, mientras que cada medición se refiere a la distancia desde uno de los dos ejes y tiene lugar en la dirección que es paralela al otro eje. Los valores de las coordenadas se calculan expresando las distancias medidas en las unidades de medida de la red y teniendo en cuenta el nivel de precisión exigido. Las distancias horizontales están representadas por el valor de la variable X, mientras que las distancias verticales o las variaciones de ubicación están representadas por el valor de la variable Y. Teniendo en cuenta cómo la ubicación de un punto específico puede describirse mediante un par de valores numéricos en un sistema ortogonal superficie, somos capaces de calcular la distancia entre dos puntos, así como la dirección de la línea recta formada por esos dos puntos, como se demuestra a continuación:
D12 = [(X1 - X2)^2 + (Y1 - Y2)^2]^(1/2)
TANa12 = [(Y1 - Y2) / (X1 - X2)]
a12 = arcTan [(X1-X2) / (Y1-Y2)]
Donde 1 y 2 representan dos puntos determinados en la superficie del Sistema de coordenadas planas y (X1, Y1) y (X2, Y2) sus valores de coordenadas. Por lo tanto, D12 representa la distancia entre esos dos puntos y a12 representa la dirección angular de la línea recta formada por esos dos puntos, como se observa que se mueve desde el punto 1 al punto 2. El símbolo TAN representa una función trigonométrica, por lo tanto, para estimar el valor del ángulo a12 uno debe calcular el arcoTAN (o TAN ^ (- 1)) para definir el valor del ángulo a12. Es una triste verdad que el desarrollo de todos los métodos descritos anteriormente y la representación sistemática de los sistemas de coordenadas en la superficie de las asignaciones fue inducido por el avance tecnológico de los sistemas de armas durante la Primera Guerra Mundial. Los cálculos que incluían valores geográficos de latitud y longitud fueron demasiado complicados para cumplir con los objetivos de los cálculos rápidos del campo de batalla y, por lo tanto, la creación del Sistema de coordenadas planas sirvió como una solución práctica.
 FUENTE
En resumen, para definir un sistema de coordenadas planas, los ingenieros deben proyectar la esfera de referencia sobre una superficie plana utilizando la proyección cartográfica apropiada. Entonces es hora de colocar los ejes primarios Ox y Oy y, por lo tanto, establecer el punto de referencia del sistema de cuadrícula donde los ejes se cruzan entre sí. El sistema de cuadrícula del mapa se construye más tarde dividiendo los ejes en partes iguales y grabando líneas absolutamente paralelas que forman cuadrados de igual área en la superficie del mapa. Los observadores ahora son capaces de calcular cualquier punto de coordenadas dado midiendo la distancia vertical del punto desde ambos ejes primarios. Esto puede lograrse en cualquier nivel de precisión demandada y medirse en cualquier sistema métrico utilizado para el cálculo de distancias en la superficie terrestre natural. Y esta es probablemente la forma más simplificada en que encontrará esta información publicada en la web. Bromeando, solo espero que sí. :)
FUENTE
En resumen, para definir un sistema de coordenadas planas, los ingenieros deben proyectar la esfera de referencia sobre una superficie plana utilizando la proyección cartográfica apropiada. Entonces es hora de colocar los ejes primarios Ox y Oy y, por lo tanto, establecer el punto de referencia del sistema de cuadrícula donde los ejes se cruzan entre sí. El sistema de cuadrícula del mapa se construye más tarde dividiendo los ejes en partes iguales y grabando líneas absolutamente paralelas que forman cuadrados de igual área en la superficie del mapa. Los observadores ahora son capaces de calcular cualquier punto de coordenadas dado midiendo la distancia vertical del punto desde ambos ejes primarios. Esto puede lograrse en cualquier nivel de precisión demandada y medirse en cualquier sistema métrico utilizado para el cálculo de distancias en la superficie terrestre natural. Y esta es probablemente la forma más simplificada en que encontrará esta información publicada en la web. Bromeando, solo espero que sí. :)
Sistemas de rejilla
Ahora analizaremos con más detalle los cuatro principales sistemas coordinados cartesianos ampliamente utilizados en los Estados Unidos hoy en día y los sistemas de grillas "cartesianos" utilizados por aquellos. Prometí en la introducción que elaboraría más sobre esto y aquí estoy para explicar que acabo de nombrar esos sistemas de grillas como Sistemas de Grillas Cartesianas debido al hecho de que los atributos geométricos utilizados y demostrados, así como las funciones matemáticas que describen su naturaleza y las propiedades se 'toman' del Sistema de Coordenadas Cartesianas y, por lo tanto, el desarrollo de esas rejillas de las que hablaremos se basó en este sistema. Eso explica por qué lo cito, simplemente estoy jugando con el significado de los términos científicos, como siempre. Hay cuatro tipos principales de sistemas de rejilla utilizados en la actualidad, como se demuestra a continuación:
- Universal Transverse Mercator Grid System (UTM)
El Sistema Universal Universal Transversal de Mercator se utiliza ampliamente en la actualidad en casos de mapeos topográficos e imágenes de satélite, así como en la creación de todo tipo de bases de datos en general, incluida la información sobre diversos tipos de recursos naturales y las correlaciones de distribución espacial entre ellos. El sistema UTM se utiliza en casos en los que se exige una alta precisión con respecto a la topología y utiliza el medidor (m) como una unidad de medida con respecto a las distancias. El sistema UTM Grid está diseñado y construido con la utilización de la proyección de Mercator de Tranvserse. Probablemente lo adivinaste. Vale la pena mencionar que fue diseñado para enfocarse en áreas de la Superficie Natural Terrestre situadas dentro de los límites establecidos por los Paralelos de 84N y 80S respectivamente.
- Sistema de rejilla estereográfica polar universal (UPS)
El Sistema Universal Polar Stereographic Grid fue diseñado para enfocarse en áreas de la Superficie Natural Terrestre situadas al Norte del Paralelo de 84N y al Sur del Paralelo de 80S, proporcionando un sistema de coordenadas y grillas que puede alcanzar los niveles de precisión del UTM. La dirección del norte en la cuadrícula es absolutamente paralela a la dirección del meridiano central. Vale la pena mencionar que las zonas de cuadrícula en el sistema de UPS se dividen en cuadrados de igual área, al igual que en el caso del sistema UTM. El UPS Grid System se construye con la utilización de una versión de la Proyección estereográfica azimutal centrada en el Polo Norte de la Tierra. Esto le da al sistema de grillas de UPS el importante atributo de preservar el factor de escala a lo largo de la dirección de Parallels.
- Sistema de coordenadas del plano estatal (SPC)
El Sistema de coordenadas del plano estatal fue diseñado y creado por el Servicio Geodésico y Costero de los EE. UU., Que en la actualidad se conoce y se conoce como el Cuadro de Estados Unidos y la Encuesta Geodésica, en la década de 1930. Básicamente inventaron un sistema de coordenadas ortogonales para cada uno de los 50 estados con el fin de ayudar a los ingenieros de topografía con el proceso de triangulación, que es una técnica utilizada para crear un sistema de puntos con coordenadas conocidas que ayudarían al estudio y desarrollo posterior de la Superficie Natural Terrestre. El sistema SPC Grid se basa en la proyección transversal de Mercator, sin embargo, hay casos en los que se utiliza la proyección cónica conforme de Lambert.
- Sistema de encuesta de suelo público (PLSS)
El Sistema de Encuestas de Tierras Públicas se diseñó en 1785, luego de que el Congreso aprobara legislación para la creación de un sistema de coordenadas ortogonales que se utilizaría ampliamente en la creación de correspondencias con respecto a los monumentos y la propiedad pública del país. El sistema de cuadrícula utilizado en el PLSS muestra diferencias fundamentales con respecto a los utilizados en los sistemas UTM y UPS. La unidad de medida principal utilizada en el PLSS con respecto a las superficies es de 1 hectárea, que equivale a 10 000 m ^ 2. Hoy el PLSS cubre áreas de la Superficie Natural Terrestre que incluyen más del 75% de la tierra situada en los 50 estados de América. Sin embargo, los cálculos son bastante complicados debido al hecho de que se utilizan las unidades de medida tradicionales de EE. UU. 1 hectárea equivale a 43 560 pies cuadrados o 1/640 millas cuadradas ...
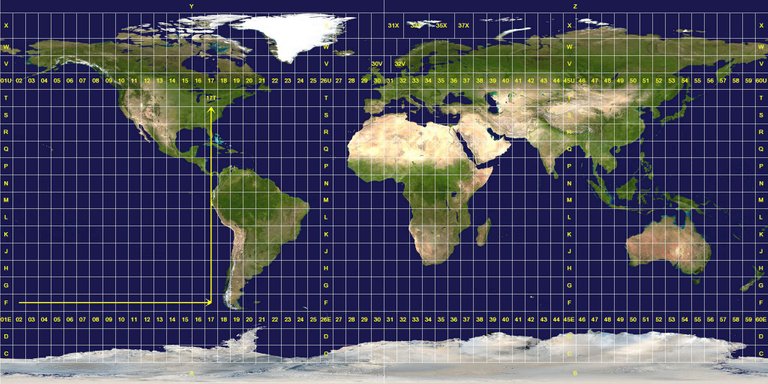 FUENTE
Bien, eso es todo por hoy chicos! Gracias por pasar por mi blog y tomarse el tiempo para leer mi trabajo. Espero que hayas disfrutado tanto como yo. Dicho esto, la octava parte de la serie Introducción a la Cartografía, en relación con las coordenadas cartesianas y los sistemas de cuadrícula, ha llegado a su fin. No dude en hacérmelo saber en los comentarios a continuación si tiene alguna pregunta y haré todo lo posible para proporcionar respuestas rápidas. ¡Sígueme por más blogs de ingeniería! :)
FUENTE
Bien, eso es todo por hoy chicos! Gracias por pasar por mi blog y tomarse el tiempo para leer mi trabajo. Espero que hayas disfrutado tanto como yo. Dicho esto, la octava parte de la serie Introducción a la Cartografía, en relación con las coordenadas cartesianas y los sistemas de cuadrícula, ha llegado a su fin. No dude en hacérmelo saber en los comentarios a continuación si tiene alguna pregunta y haré todo lo posible para proporcionar respuestas rápidas. ¡Sígueme por más blogs de ingeniería! :)






