Muy buenas amigos!! Hoy os voy a hablar sobre las dimensiones. Siempre hemos pensado que las dimensiones eran 1, 2, 3, 4,... Pero eso tan solo era la forma que teníamos nosotros de denominar a los distintos niveles de percepción de la realidad. Y como prácticamente usamos los números enteros para todo, hemos pensado que las dimensiones también son enteras y que éstas están separadas unas de otra.

Pero hoy vamos a ver cómo en realidad las dimensiones no están separadas unas de otras, y que incluso existen infinitas dimensiones entre lo que nosotros hemos llamado dimensión 1, 2, 3, 4,...
Para empezar vamos a hablar de lo que se llama la dimensión fractal. Para ello vamos a ver la "Curva de Koch":
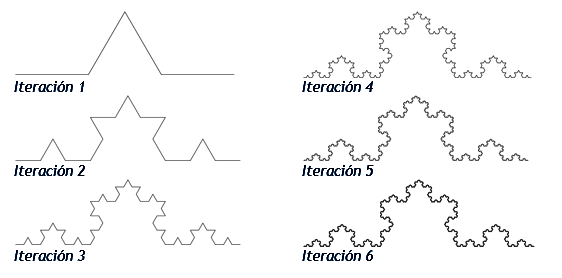
A simple vista se puede ver el proceso que se sigue para convertir una linea en lo que se llama "Curva de koch". Simplemente se divide la linea en tres segmentos iguales, y en el segmento del medio se crea un triángulo equilátero que tiene el mismo lado que cualquiera de los tres segmentos iniciales.
Si medimos la longitud de las lineas de las primeras iteraciones de la curva, nos saldrá una medida de longitud, o sea, de una dimensión. Pero ahora vamos a ver una cosa muy curiosa. Vemos que desde el principio, la curva era limitada a tres segmentos de longitud fija. Por lo que es lógico pensar que por mucho que iteremos la función, la longitud aumentará, pero nunca llegará al infinito y la dimensión serán siempre una.
Al medir la longitud de una curva de Koch iterada hasta el infinito, el resultado es infinito.
Para calcular la dimensión fractal de esta figura, tenemos en cuenta que el número de segmentos en cada iteración es "N_n = 4^n", y la longitud de cada segmento se reduce en un factor de un tercio cada vez "ln=(1/3)^n". Se dividen ambos factores y esto da como resultado la dimensión de la curva. (Tienes más información sobre cómo encontrar la Dimensión de un fractal AQUÍ)
La dimensión de la curva de Koch es Dim = 1.26186.
Esto nos hace pensar en una cosa. Si algo finito tiene dimensión fractal, entonces esas dimensiones fractales están en todas partes!! Las dimensión no son sino formas de percepción. No existen tales cosas como las dimensiones. Todo es ADIMENSIONAL. Pero por el simple hecho de estar percibiendo la realidad a través de los sentidos estamos accediendo a parte de la información del universo (la información es adimensional). Las dimensiones han sido creadas por el hombre para explicar lo que ve. Pero no hay dimensión 1, 2, 3, 4... sino infinitas dimensiones, o ninguna!!
¿Que es un espacio, sino la sucesión de infinitos planos?
¿Que es un plano, sino la sucesión de infinitas lineas?
¿Que es una linea, sino la sucesión de infinitos puntos?
¿Y cuál es la dimensión de un punto?

A pesar de todo ello, la realidad es real para nosotros que estamos inmersos en ella, por lo que necesitamos encontrar maneras de determinar las cualidades físicas de cualquier objeto, así como su dimensión. A medida que avancen los estudios sobre la dimensión fractal, veremos que éstas están por todos lados y que nosotros no estamos en la tercera dimensión, sino en una dimensión fractal aún mayor.
De hecho, la cuarta dimensión es tan solo el espacio moviéndose dentro del propio espacio. La cuarta dimensión es la que conecta todos los sucesos dentro del espacio, es lo que llamamos tiempo. Pero como ves, es solo una forma de percepción de la realidad. Y la hemos integrado y adaptado como nuestra porque es la única que hemos podido entender hasta ahora y la que ha sido capaz de explicar lo que vemos.