
Por serie de tiempo nos referimos a datos estadísticos que se registran, es decir, es el resultado de observar los valores de una variable secuencialmente en intervalos de tiempo, espaciados entre sí, así los datos usualmente son dependientes entre sí. El principal objetivo de una serie de tiempo xt donde t= 1,2…..n, es su análisis para hacer pronóstico por ejemplo, las ventas, precios de artículos, el ingreso nacional bruto, velocidad del viento, la temperatura de un proceso, series sismológicas, electroencefalograma, tasas de mortalidad, tasas de natalidad, ofertas, gastos, utilidades, series de demanda entre otros.
En efecto, en el método de una serie de tiempo, se debe hacer es representar un gráfico de secuencia; esto significa representar gráficamente cada observación xt frente al instante t en que se observa, luego unir con segmentos cada uno de los T puntos.
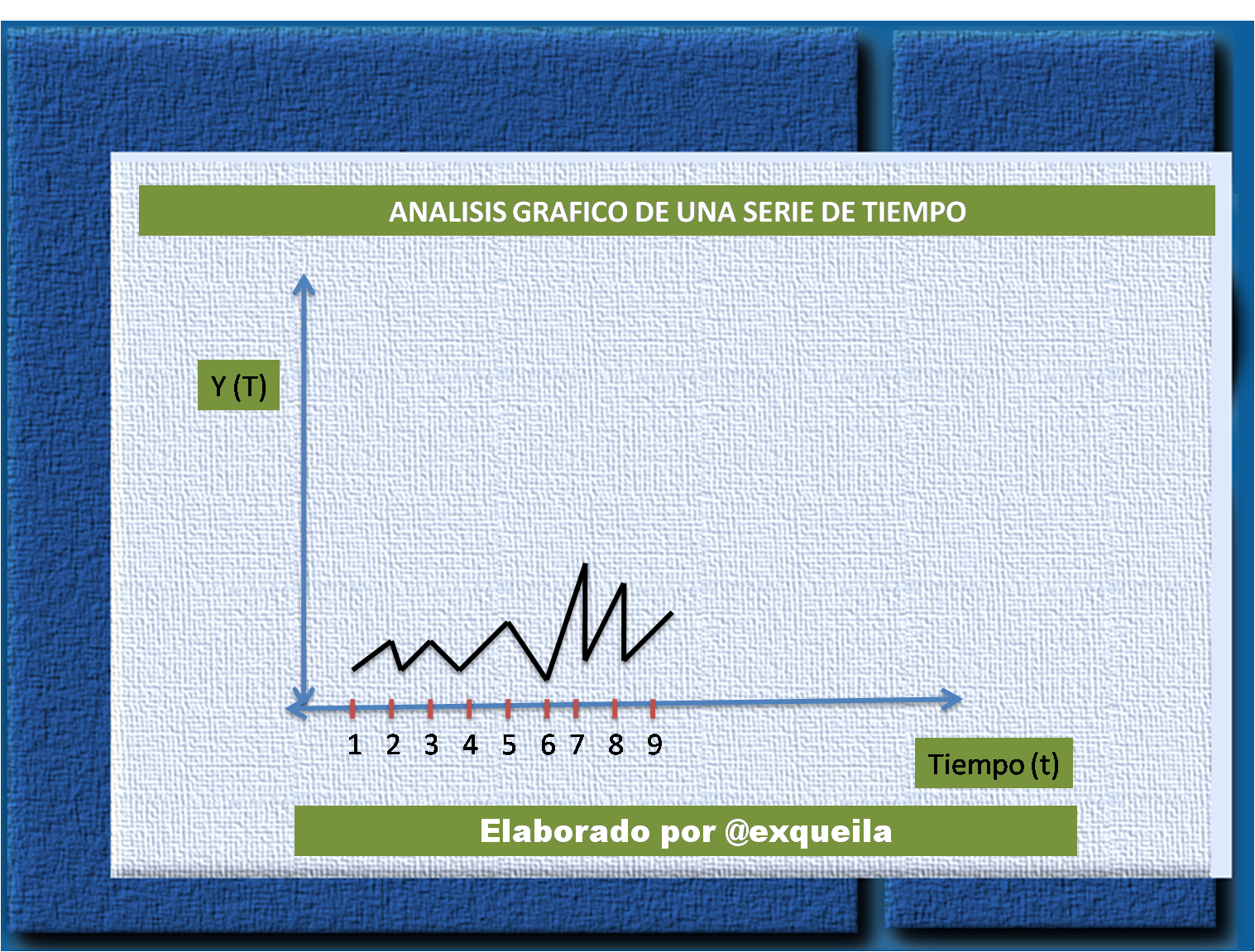
En la series de tiempo las observaciones se toman en intervalos regulares de tiempo, por ejemplo cada hora, día, mes. Se admite que la variable x ha sido observada en los instantes 1,2…..T será representada por x1,x2….xt. A su vez en una serie preexisten tres tipos básicos de variación, que contribuyen a los cambios observados en un período de tiempo y dan a la serie su aspecto errante. Estos tres componentes son:
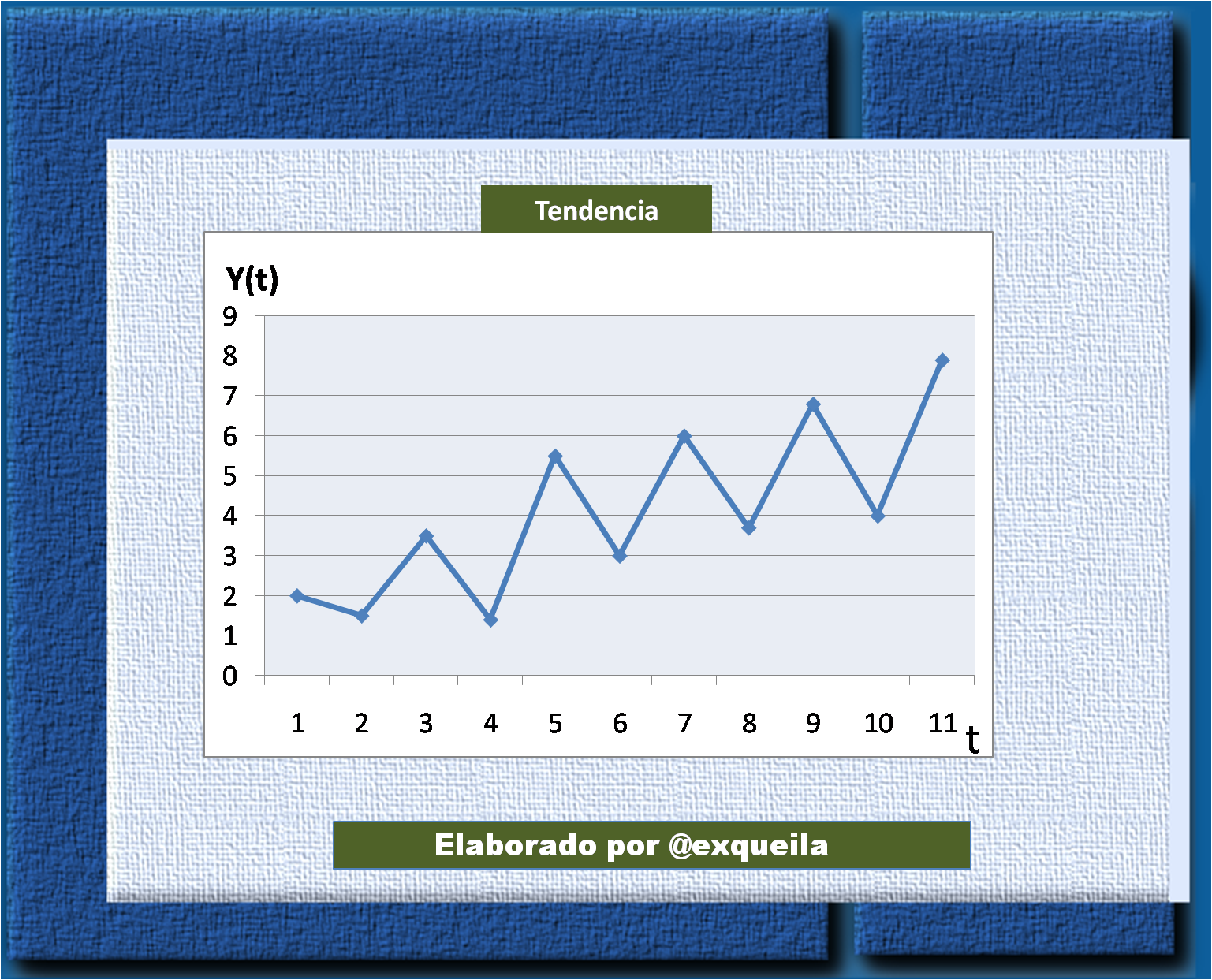
Tendencia a largo plazo:
En esta serie es común el resultado de factores a largo plazo, tales como: la población, variación en los ingresos, características demográficas. En consecuencia algunas se mueven consecutivamente hacía arriba, otras decrecen, y otras más perduran igual en un intervalo de tiempo.
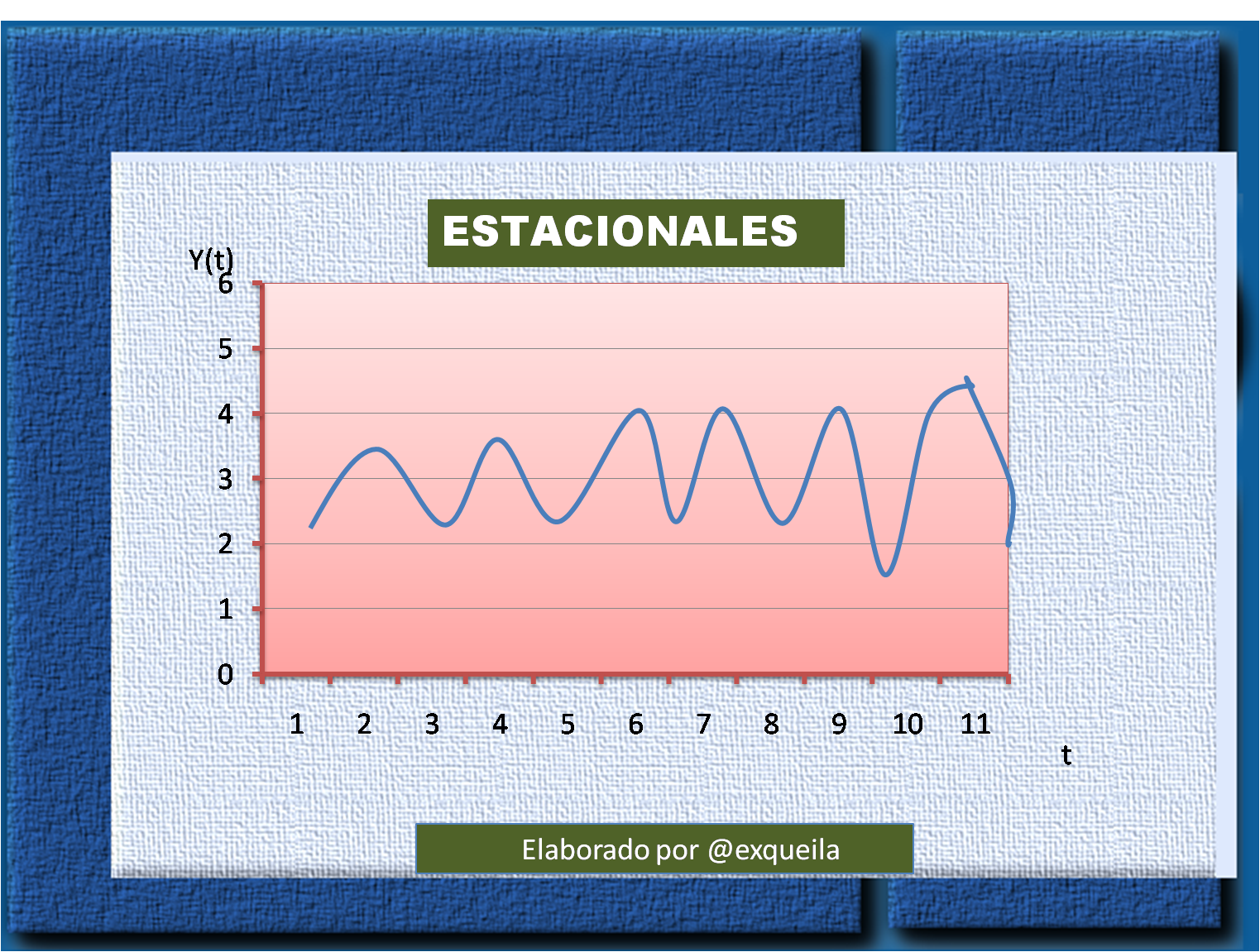
Estacionalidad:
Es el comportamiento periódico de la serie, esta variación corresponde a los movimientos de la serie que recurren año tras año en los mismos meses o en los mismos trimestres.
Heterocedasticidad:
En este caso la variabilidad de la serie depende de su nivel, las series de tiempo presentan secuencias alternas de puntos abajo y arriba de la línea de tendencia que duran más de un año. Existen dos tipos de variación irregular: las variaciones que son provocadas por acontecimientos fácilmente identificables y las variaciones aleatorias o por casualidad, cuyas causas no se pueden señalar en forma exacta. Como se señalaba esta se debe a factores a corto plazo, imprevisibles y no recurrentes que afectan a la serie de tiempo.
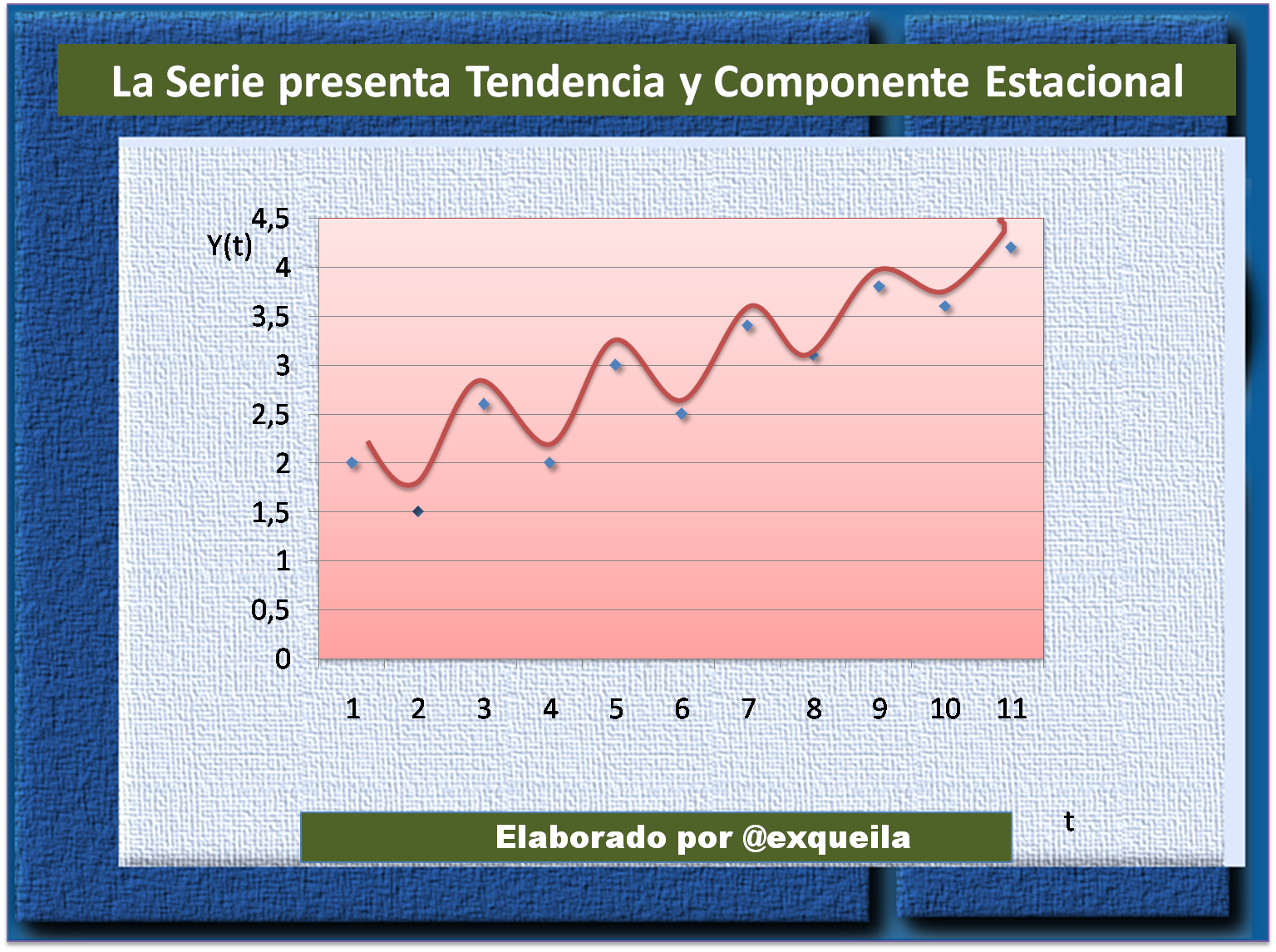
Se sugiere, independiente de cuán simples o complejos sean los procedimientos que se emplean realizar el paso más importante como es graficar la serie. Además, existe una relación multiplicativa; es decir, cualquier valor de una serie es el producto de factores que se pueden atribuir a los tres componentes mencionados inicialmente. A continuación el grafico permitirá detectar cada uno de los casos:
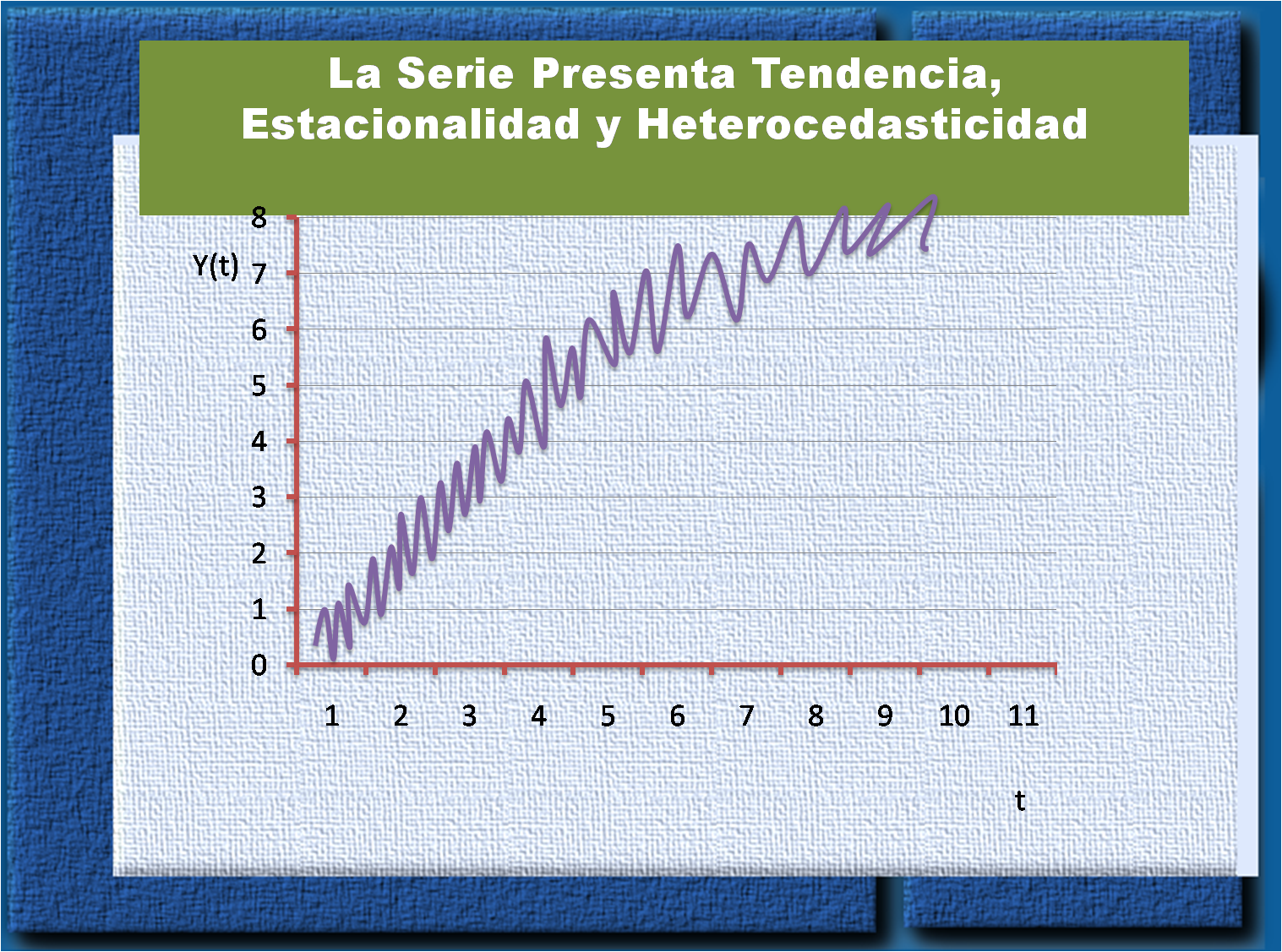
Descomposición de una serie de tiempo:
Edificar un modelo que represente de una manera espontánea la evolución de la serie a través del tiempo. Aún cuando, se adjudica que los datos xt pueden enunciarse como una función de una componente de tendencia Tt, componente estacional St y de un error at:
- Tt: Representa el procedimiento a largo plazo de la serie.
- St: Representa el procedimiento periódico de la serie.
- at: Representa a la parte impredecible de la serie.
Descomposición Clásica de una Serie de Tiempo:
La elección de uno de estos modelos se creará de modo que el modelo adoptado sea capaz de reunir las principales características, motivo por el cual hay que prestar atención en el grafico de secuencia de la serie en estudio. Para llevar a cabo la descomposición los modelos que se utilizan con más periodicidad son: Un modelo clásico de series de tiempo, supone que la serie Y(1), ..., Y(n) puede ser expresada como suma o producto de tres componentes: tendencia, componente estacional y un término de error aleatorio
- El Modelo Aditivo: Este modelo es oportuno cuando la magnitud de las fluctuaciones estacionales no varía al hacerlo la tendencia
Se descompone a través de la siguiente fórmula:
xt = Tt + St + at
- T: Tendencia de la serie.
- S: Variación Estacional.
- A: Variaciones aleatorias.
Modelos Multiplicativos:
Cuando la magnitud de las fluctuaciones estacionales de la serie asciende y desciende igualmente con los incrementos y decrecimientos de la tendencia, estos modelos son apropiados. Así mismo tenemos la clasificación de los modelos multiplicativos:
- Modelo Multiplicativos Puros: xt = Tt ×St ×at
- Modelo Multiplicativo Mixto: xt = Tt ×St + at
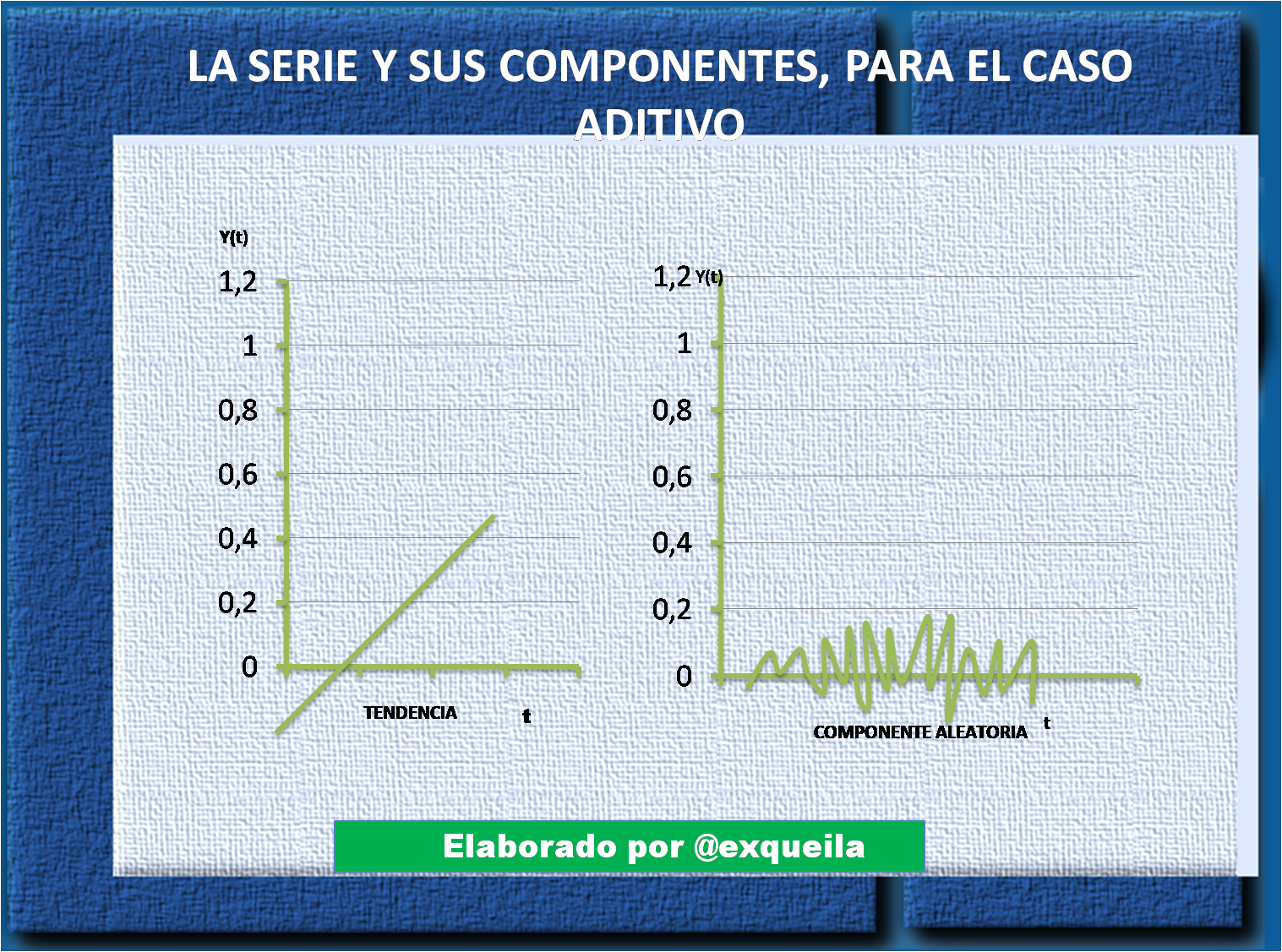
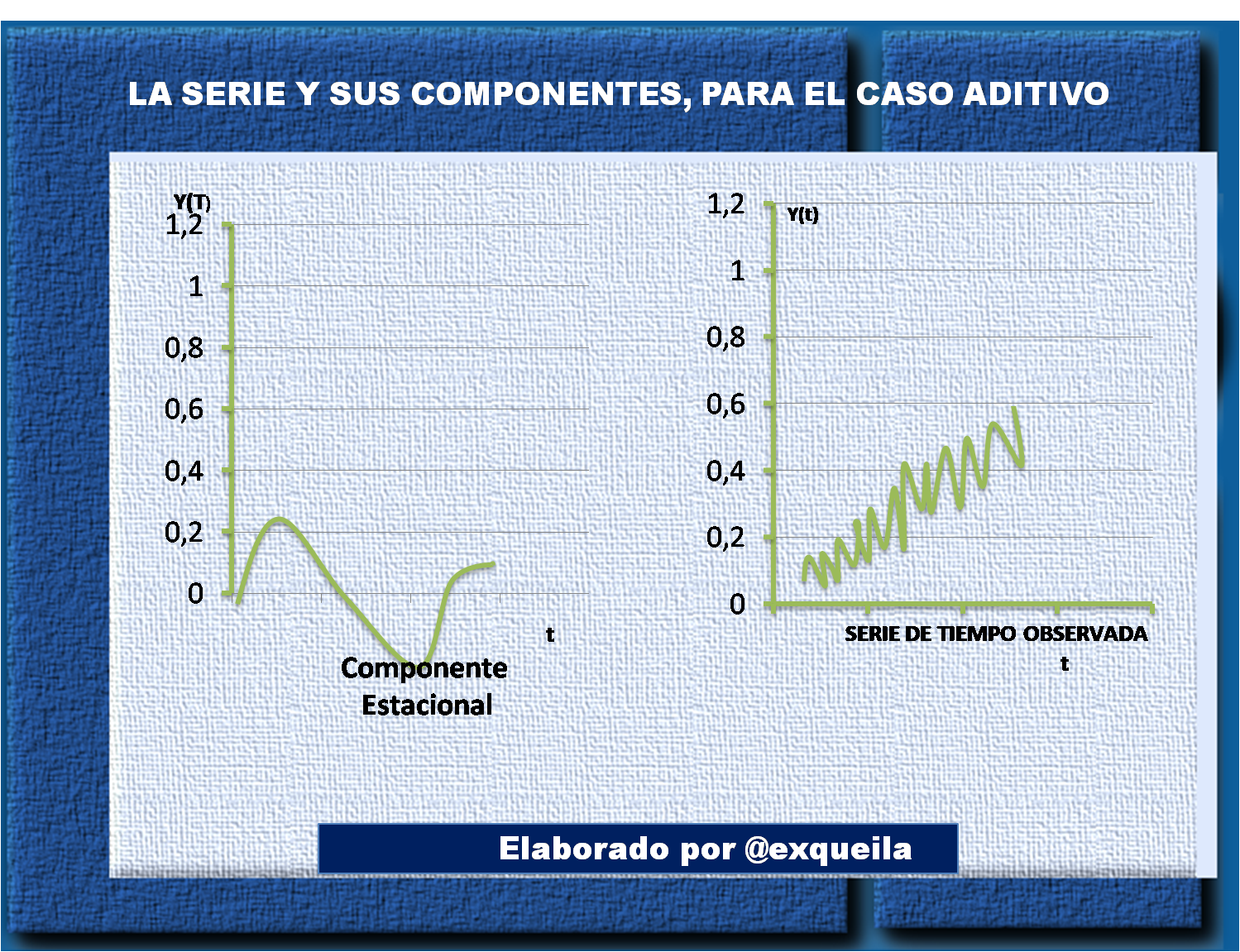
Posteriormente cuando ya hayamos seleccionado el modelo para describir a la serie de tiempo, pasamos a el segundo paso que será deducir la tendencia Tt y su componente estacional St a partir de xt el error at se consigue concisamente de estos. Si expresamos al periodo de la serie por s, entonces St = St−s. A estos elementos, para conocer la componente estacional St (t = 1,..., T) hay que conocer s de sus valores consecutivos.
Por ejemplo, conviene estar al tanto de los valores S1,...,Ss, los cuales se conocen como índices estacionales.
Se tiene que St+1 +•••+ St+s = S1 +•••+ Ss.
Métodos para aislar la Tendencia y la Componente Estacional en una Serie de Tiempo:
- Método Paramétrico: En el se expresa la relación que guardan la tendencia y la componente estacional con el tiempo. Con respecto a ajustar dichos modelos a la serie de tiempo, a través del método de mínimos cuadrados, aislar la tendencia y la componente estacional por medio de los modelos ajustados.
- Metodo no Paramétrico: Este método específicamente se basa en asumir suavidad en la relación que guardan la tendencia y la componente estacional con el tiempo. Es decir, aislar la tendencia y la componente estacional a través de la suavización del gráfico de secuencia .
En el próximo capítulo hare referencia a el método no paramétrico que suaviza a través de medias móviles. También analizaremos las Serie con tendencia y con componente estacional y sin él, componente estacional y heterocedasticidad, y el Suavizador de medias móviles con ejercicios prácticos.
Bibliografía
Peña, D. (2005). Análisis de Series Temporales. Alianza Editorial
- Referencia 5
- Imágenes y Gráficos realizados por mi autoría en el Programa de Power Point.
Lcda. Exqueila Rodriguez Díaz
Especialista en Derecho Mercantil Mención Gerencia en Talento Humano Egresada de la Universidad de los Andes
Mérida-Venezuela
Especialista en Derecho Mercantil Mención Gerencia en Talento Humano Egresada de la Universidad de los Andes
Mérida-Venezuela
Su post ha sido valorado por @ramonycajal
Que importante se ha vuelto la ciencia de los datos en estos últimos años.
Que importante se ha vuelto las matemáticas en el uso de la vida cotidiana.
También podemos observar que la ciencia de los datos se apoyan mucho en el uso de supercomputadoras para poder manejar millones de datos y poder analizarlos, cosa que el ser humano no pueda hacer con una simple calculadora.
Muy interesante los métodos de procesamiento de series de tiempos, pero que programa estadístico o informático se puede usar para predecir el comportamiento de esa serie de datos que nos dé una precisión del 100% o lo más aproximado posible cuando el conjunto de los datos es demasiado grande.
Saludos....
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
La estadística y sus aplicaciónes son cada vez mas evidentes y necesarias para la humanidad. Que difícil de explicar se torna cuando te preguntan: cual es la importancia de la estadística en una empresa? (Preguntas de estudiantes universitarios al iniciar la licenciatura en turismo). Digo difícil porque hay tantas respuestas que no se sabe por donde comenzar...
Excelente articulo...