
Imagen elaborada y editada por @centaurox
Unas de esas aplicaciones matemáticas como herramienta es la integral, la cual bajo el esquema de la teoría de integración presenta dos aspectos principales, el cálculo de integrales de funciones y la segunda la medida de conjunto. Desde el punto de vista el cálculo del área, lo que incentivo el desarrollo del cálculo integral, que se utilizó para simplificar y comprobar ecuaciones a nivel de la física, química, biología, hasta el mundo económico, lo que permitió definir ecuaciones para la operaciones, para obtener las integraciones de ecuaciones conjuntas, bajo el enfoque de método de integración.
La definición de la integral definida consistía en emplear un proceso de límite, para asignar medidas a cantidades como área, volumen, etc. Para la definición de integral doble de una función de dos variables en una región del plano, se utilizará un proceso similar, dividiendo la región en subregiones y tomando el límite cuando el número de subregiones es infinito.
El proceso anterior de integración iterada, con la definición correcta de los límites de integración, según sea el recinto de definición, será el que se utilice para el cálculo de las integrales dobles.
Cita textual del libro, Cálculo integral por José Manuel Casteleiro, Rafael Paniagua Gómez-Álvarez
pág.:425.
Análisis a través de una gráfica.
El planteamiento es el siguiente se trata de hallar tangentes en un punto de una curva C, dada una función f continua y positiva, teniendo conocimiento la siguiente relación x = a, x = b.
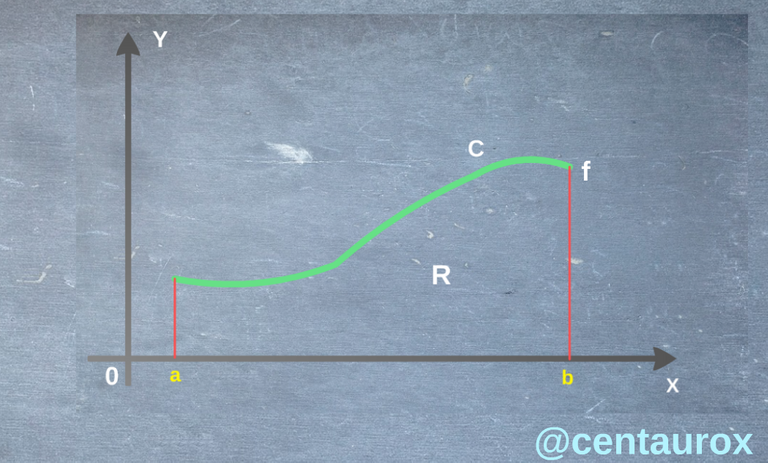
Gráfica 1 elaborada por @centaurox
En esta grafica nos muestra que la región R encerrada entre la curva C, el eje de las abscisas y las rectas de ecuaciones, x = a, x = b poseen un área, la cual mide un número de unidades cuadradas, que se encuentran dentro de la región, cuando se toma por unidad el área del cuadrado de lado por la unida, nuestra limitante es la región en R está limitada por una curva. Considerando f una función continua y definida en [a,b] sea f(x)>0, tomando como referencia el eje de las abscisa 0X y las rectas de ecuaciones, x = a, x = b, de tal forma que dividimos el segmento [a,b], en longitudes iguales de b-a/n, dando varios rectángulos tiene como base de un segmento de longitud (b-a).
De tal forma tenemos la altura de longitud f(x0),f(x1),f(x2),f(x3),f(x4),f(x5),f(x6), aparte tenemos la siguiente relación en n, los segmentos de igual longitud b-a/n, donde se considera la distancia de a hasta b teniendo como segmento de extremos tomando en cuenta los puntos a de punto de partida a + (b-a)/n hasta considerar a + k(b-a)/n y esta a su vez se establece la relación en función de X= a + (b-a)/n, para cada segmentos, que consideremos en una división particular del segmento [a,b], para este caso n=6, los rectángulos obtenidos.
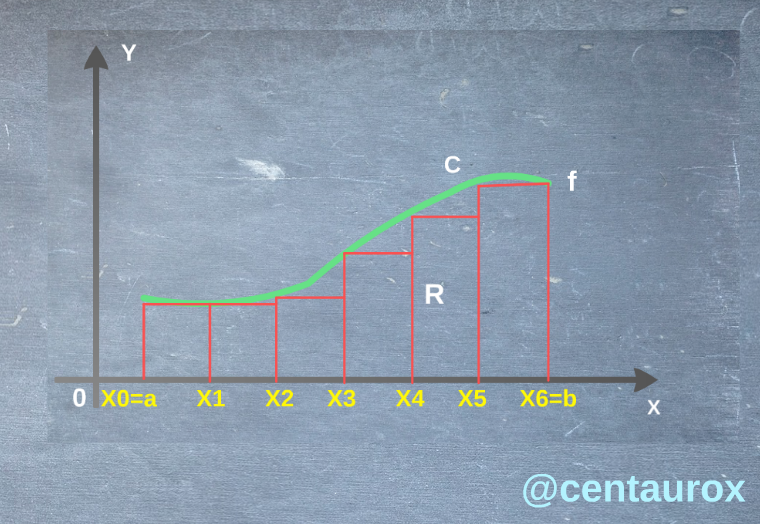
Gráfica 2. Se puede apreciar que a medida, que el ancho de los rectángulos se aproxima a cero, los rectángulos más se aproxima a la curva, por lo que la suma de sus áreas se acerca más al área bajo la curva en C, considerando f(x) es positiva y a<b. (Elaborada por @centaurox)
Usamos para para suma de las áreas la letra T6, para tener la siguiente resultante:
T6 = (b-a)/6f(x0) + (b-a)/6f(x1) + (b-a)/6f(x3) + (b-a)/6f(x4) + (b-a)/6f(x5) =
Establecemos la siguiente ecuación.
(b-a)/6[f(x0) + f(x1) + f(x2) + f(x3) + f(x4) + f(x5)] =
Tn= (b-a)/n [f(x0) hasta llegar a la expresión +f(Xn-1)]
La resultante en Tn es el valor del área encerrada por la región comprendida entre la gráfica de f, el eje de las abscisas y las rectas de ecuaciones x= x0, x=xn.
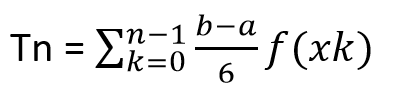
Conclusión.
Es muy importante dar a conocer la aplicación de la integral como herramienta matematica, en donde nos puede ayudar a mejor se puede usar para calcular áreas entre curvas, volúmenes de sólidos, y el trabajo realizado por una fuerza variable. En este caso vamos a ser énfasis en el calculo de volúmenes de solidos cilíndricos, por otro lado tambien nos permite en aquellas ciencias que realiza estimaciones por medio de proyecciones, nos permite analizar de manera cualitativa y cuantitativamente los diferentes fenómenos que se le presenten en su entorno cotidiano, como el caso de Economía y en Biología.
Bibliografia consultada.
Hughes, Cálculo aplicado, México, CECSA, 2004.
Cálculo integral - Página 425 por José Manuel Casteleiro, ?Rafael Paniagua Gómez-Álvarez - 2002.
Calculo Diferencial E Integral - Página 226 - 2007.
Calculus. 1,Tom M. Apostol, ?Francisco Vélez Cantarell - 2005.
Principios de análisis matemático - Página 390 Enrique Linés Escardó - 1991.
