Recomiendo leer, previamente, el siguiente post: FUNCIONES E IDENTIFICACIÓN DE VARIABLES EN EL CONTEXTO DE LA ECONOMÍA///FUNCTIONS AND IDENTIFICATION OF VARIABLES IN THE CONTEXT OF THE ECONOMY
Comencemos por definir previamente, cada una de estas funciones:
Función Costo Total: C(x)= C.F + C.V
Función Ingreso Total: I(x)=px
Función Ganancia: G(x)=I(x)-C(x)
Punto de Equilibrio.
Por ahora, vamos a manejarnos con estos tres modelos y comencemos con algunos ejemplos, aquí tenemos el siguiente problema:
Los costos fijos para fabricar cierto articulo son de $ 300 a la semana y los costos totales para fabricar 20 unidades son de $ 410. Determinar la relación entre el costo total y el número de unidades producidas, suponiendo que es lineal. ¿Cuál será el costo de fabricar 30 unidades a la semana?
Solución:
Primero identifiquemos las variables:
x: es la cantidad de artículos producidos
y=C(x): representa el costo total de producir x cantidad de artículos.
Se sabe, por los datos del problema, que C.F.= 300 y el costo variable por producir 20 artículos es de C.V.= 410
Y también se sabe que el modelo de costo es lineal, por ello, vamos a representarlo en el sistema de ejes coordenados en plan de hacernos una idea grafica del problema y así entenderlo mejor.
Tracemos el sistema de ejes coordenados, el eje de las abscisas nos va a representar la cantidad x de artículos producidos, y el eje de las ordenadas Y representara el costo de producir esa cantidad x de mercancía.
En estos problemas preponderamos el semieje positivo de las x, ya que lógicamente en estos problemas se trata de producción y venta de productos, no tiene sentido considerar valores negativos para la x.
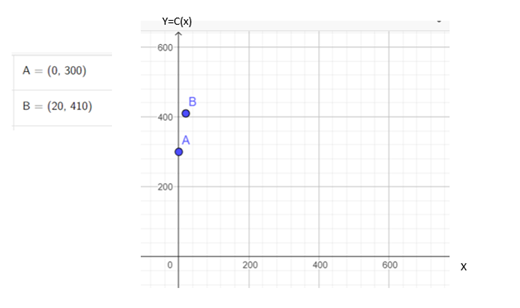
Cuando hablamos de Costo Fijo C.F. queremos decir que este es un costo permanente aun cuando no haya producción, una fábrica puede estar activa cierto tiempo y no estar produciendo, y en tal sentido su producción x es 0, pero sus gastos fijos mensuales, en este caso, es de 300. Por ello, el punto de coordenada x=0 y abscisa y=300 debe ir en la gráfica, lo llamaremos A= (0,300).
Dice el problema que la producción de x=20 artículos tienen un costo fijo de y=410; entonces el punto B= (20, 410) también debe ser ubicado en el plano.
Sabemos que el modelo de costo es lineal, en tal sentido trazaremos una semirrecta que inicia en el punto A y pasa por B.
Así:
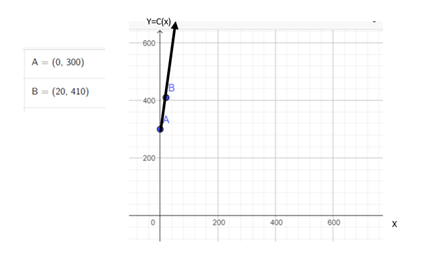
Vemos en la gráfica la descripción del problema, en ella observamos que a medida que cuando x crece (aumenta la producción) y también crece (aumentan los costos de producción), obviamente se trata de una recta creciente.
Falta la descripción algebraica de ese modelo, es decir la ecuación describe a esa recta, con ese objetivo, vamos a auxiliarnos con la ecuación Pendiente Intersección en el Origen: y=mx+b, que para nuestro caso es C(x)=mx+b
De acuerdo a la gráfica b=300, por lo tanto, nuestra función costo, hasta ahora, es C(x)=mx+300. Falta obtener el valor de la pendiente m.
Recordemos la fórmula de la pendiente, dados dos puntos P y Q por donde pasa una recta, entonces la fórmula de la pendiente viene dada por:
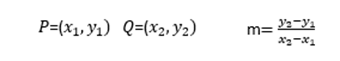
En el problema que venimos desarrollando, tenemos dos puntos: A= (0,300) y B= (20,410), aplicando la fórmula de la pendiente:
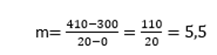
Finalmente, nuestro modelo funcional de costo es: C(x)=5,5x+300. Si queremos determinar el costo de fabricación de 30 artículos, sustituimos x=30 y calculamos C(30)=5,5.30 +300=165+300=465
Es decir, el costo de producir 30 artículos es de $ 465.
¿Si el fabricante decide vender su producto a un precio p=20,5, cual es el modelo que define a la función ingreso total?
Recordemos que I(x)=px, en este caso, sustituimos p=20,5 en dicho modelo, resultando que: I(x)=20,5x
Validemos nuestro modelo sustituyendo x=20, así: I(20)=20,5.20=410, lo cual es congruente con el problema planteado.
Y ente caso, ¿cuál es el modelo de ganancia G(x) ? G(x)= I(x)-C(x)
Sustituyendo los modelos de Ingreso y Costo anteriores, nos resulta: G(x)=20,5x-(5,5x+300)
Eliminamos el paréntesis: G(x)=20,5x-5,5x-300
Luego, nuestro modelo de ganancia es: G(x)=15x – 300
Con este modelo, podemos determinar el número de unidades que se deben producir y vender a un precio p (en este caso 20,5) para que el emprendedor pueda obtener ganancias.
Por ejemplo, si el productor fabrica y vende 20 artículos, ¿cuál será su ganancia?
Para responder a esta pregunta, debemos calcular G(20)=15.20-300=300-300=0
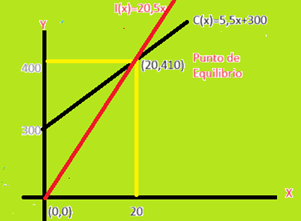
Esto le indica al productor que al producir y vender 20 artículos al precio 20, 5 dolores, no le produce ganancias, con ello solo recupera los costos. Pero, en este caso hemos llegado al Punto de Equilibrio, este punto es donde se igualan el ingreso y el costo. Es decir, punto de equilibrio es (20,410).
Si queremos ver esto en la gráfica debemos ubicar dos puntos por donde pasa la recta de ingreso, uno de ellos es (20, 410) y el otro es (0,0) ya que el ingreso de 0 es I(0)=20,5.0=0.
Veamos:
Para que el productor pueda ganar debe cumplirse que G(x)>0, es decir:
15x – 300>0
Resolviendo la desigualdad, nos queda que: 15x >300 x >300/15 x >20
Es decir, el productor deberá producir y vender 21 artículos o más para poder obtener ganancias.
En el caso de que produzca y venda menos de 20 artículos tendrá perdidas.
Esto sucede cuando 15x – 300<0
La siguiente gráfica resume los resultados:
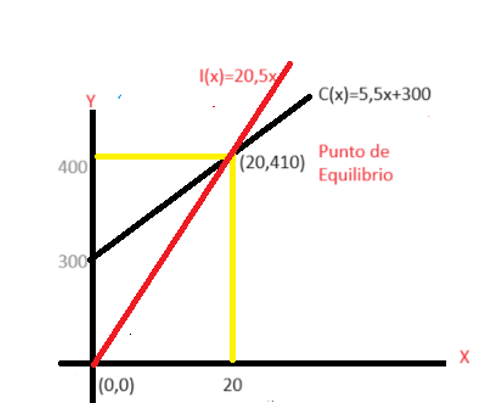
Créditos:
El post es totalmente original de la autora.
Las gráficas fueron elaboradas con el apoyo de Geogrbra y Paint
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail., apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA