Introduction
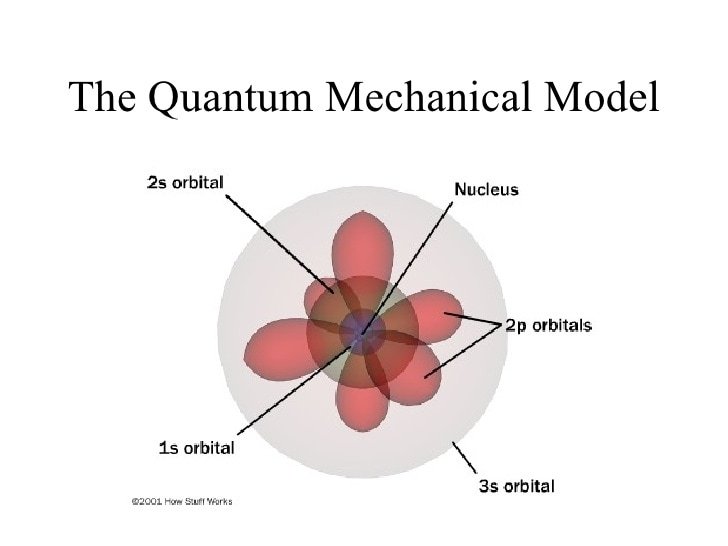
Quantum chemistry is an application of quantum mechanics which seeks to better explain the physical phenomena we understand through chemistry. It takes advantage of principles understood from physics and compares them through quantifying the trends observed in chemistry. Today we will take a look at how quantum chemistry can help us define electron orbitals.
The goal for quantum chemistry is using quantum mechanics to describe the forces which ultimately make all of chemistry possible. However, because of the complexity of quantum mechanics, it is necessary to sacrifice a degree of accuracy in order to make the equations more specialized for chemistry and at times is even necessary to make them solvable. Two of the major assumptions which are always used in quantum chemistry are that an atom's electron field is independent from its nucleus, and that each electron moves independently. By making these assumptions, it becomes possible to predict the position of electrons and therefore, the electron orbitals.
The wave function for an electron can be calculated by relating it to its energy operator through the Schrödinger equation.
The Schrödinger equation is dependent on three variables called the quantum numbers. They are the principal quantum number (n), angular quantum number (l) and the magnetic quantum number (m). It is important to note that the quantum numbers are always whole numbers and that the principal quantum number (which describes the energy level) can never be zero. As we will see, different configurations of the quantum numbers are responsible for the various electron orbitals.
First, by using the necessary assumptions, the Schrödinger equation can be rewritten as the product of two equations known as the radial, and angular wave functions. By analyzing these two components, the shape of different orbitals can be determined with the angular wavefunction and the likelihood of the electron being in different positions can be calculated with the radial wavefunction.
S Orbitals
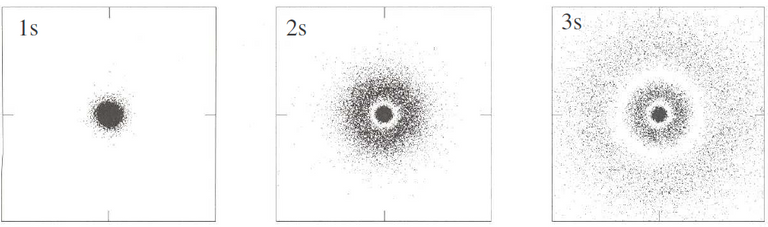
In an s orbitals, the only quantum number is the principal quantum number. This implies that the angular wave function is a constant and that the only variable in the Schrödinger equation is the radial wave function. This results in a spherical orbit as the orientation is independent of the electron distribution. The following diagram is of a simulation for electron density in different s orbitals. The three panels below depict how as the principal quantum number increases, the electron gains energy and is more likely to be farther away from the nucleus.
In p,d, and f orbitals, the angular quantum number is set at a non-zero value and the magnetic quantum numbers is allowed to have non-zero values. This makes determining the electron orbital becomes more complicated. In summary, the angular quantum number describes the number of directions regions of high electron density extend in while the magnetic quantum number describes the direction of the magnetic field.
P Orbitals
In p orbitals the angular quantum number is always one. However, the magnetic quantum number is allowed to be either 0, -1 or 1. This results in three possible arrangements which can be described as “peanut” shaped orbitals centered around the x,y, and z axis for each of the three possibilities for the magnetic quantum number.

D Orbitals
In d orbitals, the angular quantum number is set at two while the magnetic quantum number is allowed to be 0 or an integer from -2 to 2. The angular quantum number reflects there being two pairs of bulges in d orbitals which are generally oriented in two dimensions. Because of the five possibilities for the magnetic quantum number there are also a total of five possible orientations.

F Orbitals
F orbitals are by for the most complicated and are only present in the very large and unstable elements which are classified as the the lanthanoids and actinoids. Although there are more possibites, f orbitals follow the same basic pattern as d orbitals. First off, their angular quantum number is three which explains why they can point in three dimensions. Their magnetic quantum number is any integer ranging from -3 to 3 which gives them seven possible orientations.

If you have any questions or know anything you would like to add feel free to do so in the comments! Or if you have any suggestions on how I can improve I would love to hear them!
If you enjoyed my content, please consider upvoting to help others find my content or even follow me if you would like to hear more!
Work Cited:
http://www.msg.ameslab.gov/tutorials/quantumintro.pdf
http://chemistry.tcd.ie/staff/people/sd/lectures/MO_lecture_course-2.pdf
http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch6/quantum.html
https://en.wikibooks.org/wiki/General_Chemistry/Shells_and_Orbitals#The_f_orbitals

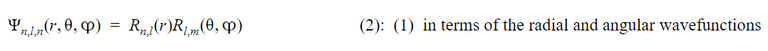
@originalworks
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!