Welcome to the "Paradox is fun!" series. In each post, I will share one interesting math paradox at a time. When we see a paradox, usually at first sight the answer seems obvious but most of the time it turns out that the solution is counter-intuitive! If you like my posts, please upvote, resteem and follow me @manfredcml : )
Boy or Girl?

(Picture source: https://nameberry.com/blog/16-crazy-baby-names-youre-going-to-be-hearing-a-lot-more-of)
Let's look at a simple probability problem:
Andrew has 2 children where the older child is a boy. What is the probability that both children are boys?
For the argument to be complete, we have to impose some assumptions. First, each child has equal chance of being a boy or a girl. Second, the sex of one child is independent of the other. What answer do you get? Let's see a straightforward derivation by considering the following table:
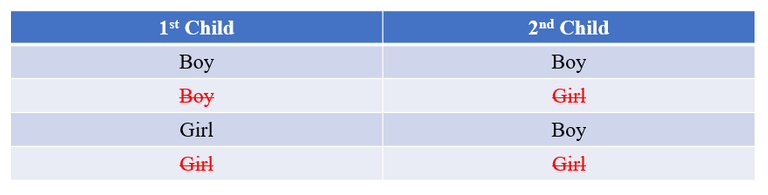
For simplicity, I will abbreviate "Boy" as "B" and "Girl" as "G". There are 4 possibilities from the table above, namely (B, B), (B, G), (G, B) and (G, G) respectively. Clear (G, G) is not possible. We assume the second child is the older child (indeed it does not matter whether the first or second is older in our argument). Then, (B, G) is not possible as well. Of the remaining 2 possibilities (the first and third row of the table), only the first row corresponds to both children being boys. So the answer is 1/2.
Look straightforward? Let's see a variation of the first problem:
Andrew has 2 children where one of the children is a boy. What is the probability that both children are boys?
What's your first sight? It is intuitive to guess 1/2 as the answer. But is it true? Let's draw a table again:

Again (G, G) is clearly not possible. Since we are given that one of the children is a boy, (B, B), (B, G) and (G, B) are also possible. It follows that the probability of both children being boys are 1/3.
Now we should get the brief idea of the "trick" of this paradox. To see the even more interesting part of this paradox, let's consider one more variant:
Andrew has 2 children where one of the children is a boy and that boy was born on a Tuesday. What is the probability that both children are boys?
Hey what? That guy was born on Tuesday? How does it relate to the problem at all? That's the fun of this paradox! We impose 2 more natural assumptions: first, the birth date of a child is independent of another child; second, the probability that a child was born on any given day of a week is 1/7. I am not going to show the steps here and will leave it for you to try : ) Basically, the idea is the same as the above 2 examples. The answer is 13/27, a surprising number!
Short note
If you treat the above discussion in the strictest mathematical standard, you may find some mathematical ambiguity in the setting of the problems. Yet, in this post I only try to show the core idea of the paradox without doing all the math in the most rigorous level. If you are interested in a formal treatment of this paradox, please refer to the reference I show below : )
Coming soon...
In the next post, I will share with you the interesting and classical Monte Hall problem!
Reference
Wikipedia - Boy or Girl paradox
I write articles on machine learning, applied statistics and economics to the best of my knowledge : ) If you like my posts, please upvote, resteem and follow me @manfredcml.
Other articles:
Be a smart gambler! #1 - Gambler's fallacy
Let's play a game #1 - Prisoner's Dilemma