The Intricacies of Infinity - Hilbert's Hotel

Hey guys how are you? To motivate today's topic let me ask you a brief question:
Does the set of natural numbers contain more elements than the set of
even natural numbers?

At this point many people might be inclined to respond with.
'Yes, of course! Clearly the former set is a contains both even and odd numbers
so how could it not have more elements?'

But mathematically speaking the answer the answer is:
No, both sets contain the same number of elements, namely countably
infinitely many.

Pixabay

Counting in mathematics

When mathematicians attempt to quantify the number of elements in a given set they talk about cardinality.
One says that 2 given sets have equal cardinality if there exists a bijection between the two, meaning a one to one correspondence between elements of both sets.
In the above example such a bijection is easily contructed by mapping natural number n to even natural number 2n, so 0,1,2,... to 0,2,4,... respectively.
Whenever a set A's cardinality is equal to the cardinality of the natural numbers (ℕ) we describe this set as countably infinite and write |A| = ℵ₀.
This last symbol ℵ₀ is called Aleph nought and denotes the "lowest order of infinity".

Pixabay

Hilbert's Hotel

A verny nice thought experiment intended to illustrate the intricacies of counting and infinity to his students was devised by David Hilbert (1862-1943), one of the most influential mathematicians of the 20th century:

Suppose you are the manager of a hypothetical hotel with countably infinitely many rooms, for simplicity with consecutive enumeration 0,1,2,... , each with a capacity of one.
Let us (unless otherwise stated) assume that this hotel is already filled to capacity with every room occupied by one guest.

David Hilbert, Wikipedia

1. A new guest arrives

Now a new guest arrives for his stay in your hotel, how can you accomodate him?

Well technically all of the rooms are booked out and unavailable but since you have infinitely many you can do the following:
Let all of the previous guests move from their respective current room number n to n+1. In other words shift the current guests from rooms 0,1,2,.... to 1,2,3,... . This will leave room 0 empty for the new arrival and everybody else will be accomodated in his new room.

Of course this may be extended analogously to finitely many new arrivals but it gets more interesting:

2. Infinititely many new guests arrive

Suppose a coach with countably infinitely seats and passengers arrives and each of them wants to have a room. What do you do now?

This part is inherently connected to the introductory question we have discussed above. In particular the union of 2 countably sets is also countable infinite, you just have to count smartly.
Clearly our approach from part 1 does not work here, there is no well-defined way of shifting your current guests by infinitely many rooms (to define a map you'd have to specify which guest goes to which room, but there are no rooms with indices "infinity+1", "infinity+2" and so on).
What you can do is "interlacing" current and new guests. Sending each current guest in room n to room 2n will open up all odd numbered rooms 2k+1 (countably infinitely many) for the new arrivals and leave erveryone with a room.

Again, this procedure may be extended to a finite number of coaches with infinite guests arriving. But what if it gets even trickier?

3. Infinitely many coaches arrive

Suppose the hotel is on the shore and a ferry brings new guests. Specifically it carries countably infinitely many coaches with countably infinitely many passengers each - and everyone demands a room!

You might be tempted to repeat our solution from part 2 now. But the iteration of this operation (interlacing old and new guest) is only well-defined for a finite number of repetitions. Plastically speaking, to handle infinite iterations you would once again have to know which map this amounts to and who goes to which room in the end. Otherwise you will just end up interlacing guest for all eternity with no conceivable final state.

But let us agree that you can always create countably infinitely many free rooms by sending n to 2n as above. Without loss of generality one may thus just ignore the old guest for the moment and argue as if the hotel was empty.
One thing which will work is the sending people to different prime number powers:

• Passenger n₁ of the 1. coach to room 2^n₁+1, so passengers 0,1,2,... to rooms 2,4,8,...
• Passenger n₂ of the 2. coach to room 3^n₂+1, so passengers 0,1,2,... to rooms 3,9,27,...
• Passenger n₃ of the 3. coach to room 5^n₃+1, so passengers 0,1,2,... to rooms 5,25,125,...
• ...

This will even leave infinitely many rooms open and because of the uniqueness of prime factorization no room will be assigned more than once.

If you want to assign rooms more economically though you need to us e what is called a pairing function to "enumerate" the ℕ×ℕ new arrivals by ℕ rooms in a 1:1 manner.

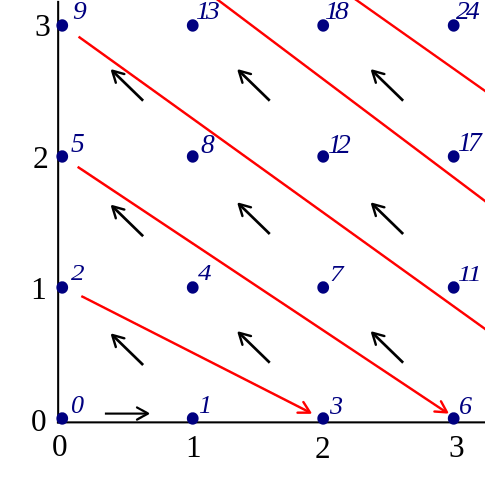
Cronholm144, Pairing natural, CC BY-SA 3.0

As you see in the picture, this can be done by progressing though all pairs of natural numbers "diagonally", e.g.

This corresponds to passenger 0 of coach 0 going to room 0, passenger 0 of coach 1 going to room 1 and so forth.
This procedure working out thereby shows that even the union of countably infinite "copies" of an countably infinite set are still countably infinite.

As it turns out you have to "escalate" step 3 infinitely many times to obtain the prototype of a truly uncountable set:
ℕ^ℕ := ℕ×ℕ×ℕ×ℕ×... is the set of natural number valued sequences and has cardinality |ℕ^ℕ| = ℵ₁, which is the "next higher order of infinity" and also corresponds to the cardinality of the real numbers.
As the subscript index suggests it does not stop here, there are ever larger Alephs which represent cardinalities and infinities far beyond the wildest imagination, but maybe this is a story for another time.

I hope that you have learned something new and have a nice day!

References:
Cardinality, Wikipedia
Pairing function, Wikipedia
Hilbert's Hotel, Wikipedia