Scanning Tunnelling Microscope
Scanning Tunnelling Microscope(STM) is an instrument with which one can make images of a surface at atomic resolution. With this device the structure of molecules can be examined. Like the image of HOPG(Highly oriented pyrolytic graphite, layered Graphene basically):
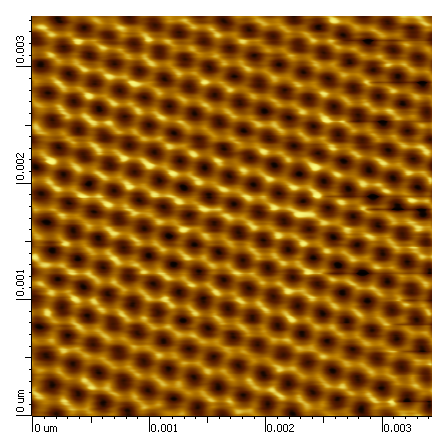
The result of a STM measurement of HPOG. The hexagonal structure is the graphene molecule[1].
For a good STM the resolution is around 0.1 nm lateral and 0.01 nm depth[2]. At this resolution the individual atoms are visible, and one can even "write" text in a font size of an atom(An image of this is placed at the bottom of this page).
How these images are made, and the purpose of them, is the subject of this post. First there is a quick description of the device followed with a more extensive physics explanation.
STM the Device
The STM isn't an extremely hard device to engineer. It doesn't costs that much, and has since its debut in 1981 transformed from an cutting edge machine to something found in classrooms. Well, classrooms at universities that is, but that is a great feat.
The microscope works by probing a tip near the surface of a sample. This tip is very sharp, ideally 1 atom in width. Bringing the tip within a few nanometers distance of the sample and applying a potential difference between the tip and the sample, will make electrons tunnel from the sample to the tip. That is, if the tip is the positive part of this potential difference, if not, electrons will tunnel towards the sample. The tip will be moved over the sample, so an area can be scanned and be imaged. Because the steps the tip has to make are in the nm range, using piezo electric motors is the only way to do this.
The schematic of a scanning tunnelling microscope is imaged below:

This is the schematic view of a scanning tunnelling microscope[2].
Of course there is an amplifier and a processor in the setup. The amplifier is to amplify the tunnelling current because it is so low, but I will ignore the amplifier and the processor in this post.
STM physics
Quantum mechanics is the foundation of the scanning tunnelling microscope. Because tunnelling is quantum mechanic in origin. So to understand tunnelling, a bit of quantum mechanics will be needed.
The Schrodinger equation is the origin of quantum mechanics, it describes a physical system and its changes over a period of time. One of the forms of the equation is:

A little bit rewritten than the source[3].
In this equation t is the time in seconds, r is the three dimensional location vector, h the Dirac's constant and E the total energy of the system(Hamiltonian).
It should be noted that every particle in the universe has the same wave-particle duality like photons, this is essential, this is explained according to the Broglie[4] which states wavelength = h / p, in which wavelength and p is the impulse.
And lastly, before we will examine tunneling, is knowing about Heisenberg. And no, I am not talking about breaking bad. Heisenberg stated that there is no way to know both impuls and location of a given particle / photon or time and energy. For now, we only focus on the latter. The uncertainty is given in:

Heisenberg's uncertainty[4]
Herein lies the key to tunnelling. And we are finally there, but first we need to talk about potential wells.
The potential wells will be drawn in 1D because this problem can be tackled 1D the easiest.
A potential well is best thought of as a valley between two mountains. Imagine a ball in the valley, and that it takes a minimum of energy to be kicked over the mountain, we will call this the barrier energy. Any energy lower than this will make the ball roll back into the valley. This feels natural and this happens in the macroscopic world according to Newtonian mechanics. But in the quantum world, this is not necessarily the case(Heisenberg). There is a certain chance a particle will be able to go through the mountain and be in another valley. This is called tunnelling and is artistically imaged below:
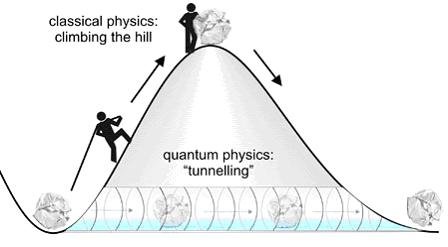
See how the tunnelling particle is passing without the needed energy[5].
Of course tunnelling doesn't happen all the time and is restricted to special cases. The equations to do se are:
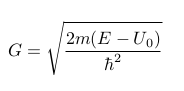

Tunnelling equation[4].
Herein is G the ratio constant, T the transmission, m the particle mass(electrons), E the particle energy, U0 the barrier energy and l the tunnel distance . This may look strange, because the number in the root is a negative, but the imaginair i takes care of that(the next paragraph will tell more). The approximation also clearly shows that increasing the distance exponentially lowers the tunnel chance, and decreasing the distance exponentially increases the tunnel chance.
The next paragraph is a quick solution for the Schrodinger equation, it gives a more in depth view of the mechanics, but you can freely ignore it.
Potential Barrier
Instead of talking about valleys and mountains, it is easier to talk about a potential barrier. Such a barrier is visible below:
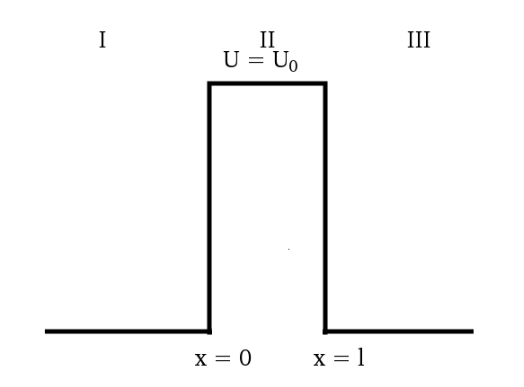
A potential barrier, which starts on the left side, with the barrier between x = 0 and x = 1, and the 0 potential at the right side of x=1. [6]
When approaching the barrier, there is a chance to enter it, and a chance to pass into it(Heisenberg at it again). The solution for the Schrodinger equation for Area I:
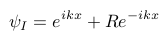
Solution area I[7].
Herein R is the amplitude constant, k the wavenumber and x the length of the area.
Area II:
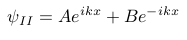
Solution area II[7].
Herein A and B are amplitude constants.
And the solution for area III:
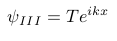
Solution area III[7].
Herein T is another amplitude constant. I apologise for using the same letter for 2 definitions.
In equation of area I and II you see a negative exponent in the Euler formulation, this is there to note a reflection on the edges of the barrier. If these were not present, all particles would mathematically tunnel, which obviously and luckily doesn't happen. In area III there is no such reflective exponent because there is no tunnelling back(presumably).
The wavenumber for area I and III are given by:
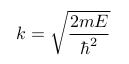
Wave number for Area I and III[7].
And for area II the potential of the barrier has to be taken in consideration:

Wave number for Area II[7].
Relevance of the images
Scanning tunnelling microscopy helps to confirm whether we the current understanding of physics is correct. Take a look at the first STM image posted at the beginning of the post, and to the theoretical representation of HPOG below:
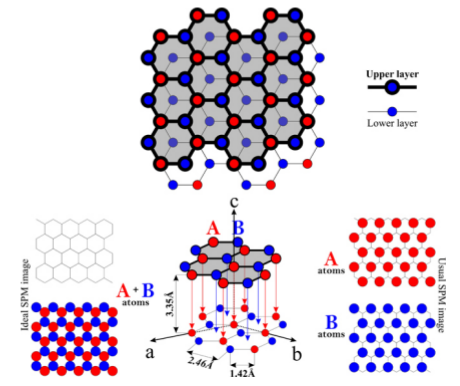
HPOG theoretical representation[8].
When compared with the image from STM measurements, one can see the hexagons. The black spot in the middle actually hides an atom from the layer below, and some of the carbon atoms are pushed upwards due to having an carbon atom underneath, and of course, some are lower because they are not pushed up. That also gives the distinctive brightness difference.
There are also other techniques like atomic force spectroscopy, that act on the same scale and measure resistance force. All these techniques help the scientific community to better their understanding of the universe at the end of the day.
Final words
The scanning tunnelling microscope is a fantastic way to show how quantum mechanics work and that it really works. When I was working with the microscope I was amazed at the elegance a rather cheap measuring device gave. Although it doesn't work with all materials, it gives a great insight in our understanding of physics before we could effectively map them.
But it is not an easy device to work with, not because of the physics, but of the maintenance. If you ever need to use such a device, I would advice you to order the tips, instead of making them yourself. Although the manual says it is easy, it is really not and your results will not be as great as the images I provided.
And as I promised, I will post a few STM images.
Since this is my first big post, please tell me what you liked or didn't like. I am willing to post more, but I want to know what is appealing and what is not. Have a nice day!
STM images
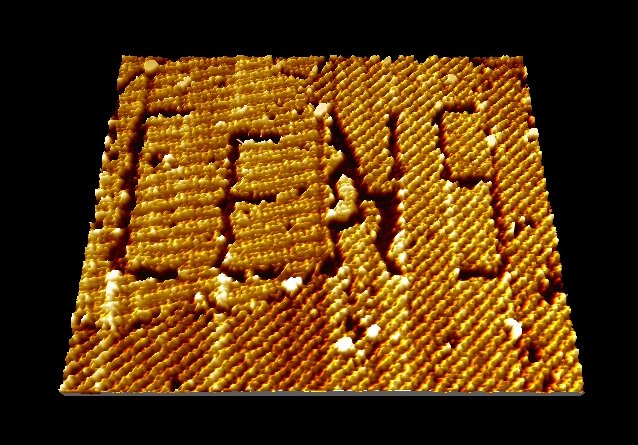
CENS was written here[2].

Gold grains, electrons in gold are evenly distributed, so making out single atoms is not possible[9].
References
[1] http://www.aist-nt.com/content/stm-hopg
[2] https://en.wikipedia.org/wiki/Scanning_tunneling_microscope
[3] https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation
[4] Douglas C. Giancoli, Physics. Peason, 4th edition.
[5] http://fuckyeahphysics.tumblr.com/post/1480703230/stuff-im-learning-quantum-tunnelling
[6] My best paint skills
[7] http://quantummechanics.ucsd.edu/ph130a/130 notes/node152.html
[8] http://nanoprobes.aist-nt.com/
[9] http://www.anfatec.net/anfatec/stm/stm.html
Wow! Really nice job! I especially like reference 6 (thought powerpoint is easier to manipulate for such an image then paint!). A very detailed look at SEM, an very heavy in the theory.
Thank you! I wouldn't know how to do that in power point, I will keep it in mind. And do you think I should have posted a bit less theory?
It depends on what your audience is! If you are going for attracting a more technical audience then more theory is better, but if you are trying to explain things to a more general audience then you want to go for more of an overview as the detailed theory will be a bit beyond their understanding.
Like how many people on the street know about the hamiltonian operator?
Yeah that is true, this isn't a science site per definition.
Thanks a lot for telling me about this article in another comment and, of course, for writing it in the first place. Very well done. And once again it has way too few upvotes.
It's a very sad fact that you would have gotten hundreds of votes more for posting some food pictures or memes.
Thanks, I am glad you enjoyed it. I commented it because I remembered you being interested in a post about this.
And about the votes, well, that is the general liking, people use the internet more for fun, but that is all good.
Very INTERESTING @chessmasterhex
You have been PROMOTED FREE for using the "resteem" TAG (hashtag)
https://steemit.com/promoted/resteem
Resteem...
Thank you very much!
My pleasure @chessmasterhex
Keep STEEM N ON,
Frank
Wow! It's a great job! I enjoyed, thank you! Resteemed!