
In diesem Artikel werden die Grundlagen der Zuverlässigkeitsanalyse erläutert und veranschaulicht dargestellt.
Inhalt
- 1 Grundlagen der Zuverlässigkeitanalyse
- 1.1 Fehlertypen und -Klassen
- 1.2 Methoden der Zuverlässigkeitsanalyse
- 1.2.1 Zuverlässigkeitsanalyse bei konstanter Fehlerrate
- 1.2.2 Zuverlässigkeitsanalyse bei variabler Fehlerrate
- 1.2.3 Generelle Initialisierung, Bibliothekimportierung und Konfiguration
- 1.2.4 Implementierung der Familie der Weibullfunktionen
- 1.2.5 Plot: Weibull - Dichtefunktion
- 1.2.6 Plot: Weibull - Verteilungsfunktion
- 1.2.7 Plot: Weibull - Harzadfunktion
1 Grundlagen der Zuverlässigkeitanalyse
Die Analyse der Zuverlässigkeit ist die Betrachtung des Versagens von Komopenten und Systeme. Die Funktionen und Kennwerte der Zuverlässigkeit sind hilfsmittel zur Bewertung der Sicherheit, Verfügbarkeit und Instandhaltbarkeit. Im Automoiv-Berich steht oft die Sicherheit in Form der funktionalen Sicherheit im Fokus.
Nach DIN 40041:1990-12 wird die Zuverlässigkeit wie folgt Definiert.
„Beschaffenheit einer Einheit bezüglich ihrer Eignung, während oder nach vorgegebenen Zeitspannen bei vorgegebenen Anwendungsbedingungen die Zuverlässigkeitsforderung zu erfüllen.“
Des Weitern kommt die Analyse der Zuverlässigkeit zugleich als Untersuchungsmethode der Fehlerursache im Qualitätsmanagement zum Einsatz. Hierbei steht die Minimierung der vermeidbaren Fehler im Vordergrund. Es hat sich jedoch herausgestellt, das einige Fehler schwerer auffindbar und behebbar sind als andere. Gründe dafür sind eineseits das sich einige Fehler prinzipiell nicht vermeiden lassen und zum anderen, dass bei einem wilkürlichen oder genauere gesagt rein zufälligen auftreten von Fehlern die Usache nicht nachvollziehbar ist. Dies führt zur Klassifiezierung und nähren Betrachtung von Fehlern.
1.1 Fehlertypen und -Klassen
Fehler lassen sich durch unterschiedliche Betrachtungsweisen typisieren bzw. klassifizieren.
Zum einen wäre dies die Betrachtung in welcher Form sie Auftreten.
- Systematische Fehler
- Zufällige Fehler
Eine weite Kategorisierung ist die nach dem zeitlichen Verlauf des auftretens der Ausfälle.
- Frühausfall
- Zufälliger Ausfall
- Verschleiß- / Alterungsausfall
Hierbei ist ein starker Zusammenhang zu den vorhergenden Fehlertypen erkennbar. Es können die zufälligen Fehler als konstant über die Zeit angesehnen werden und die Systematischen Fehler jeweils zu den Frühausfälle und Fehler durch Verschleiß und Alterung zugeordnet werden.
Beim genauen Betrachten der Aussfallkategorien wird ersichtlich, dass Frühausfälle oft herstellungsbedingt sind und über die Zeit durch eine bessere Beherschung des Herstellungsprozesses stark nachlassen. Das Auftreten von Verschleiß- und Alterungsausfälle sind hierbei stark von der Komponent abhängig und treten erst gegen ende der Lebensdauer auf und lassen sich nicht vermeiden sondern ausschließlich verzögern.
1.2 Methoden der Zuverlässigkeitsanalyse
Es hat sich etabliert die Zuverlässigkeit von Systemen und Komponenten anhand der Ausfallrate zu Bewerten.
Dabei gibt die Ausfallrate die Wahrscheinlichkeit an, mit der eine menge an Einheit in einem definierten Zeitintervalls ausfällt. Diese Betrachtungsweise bietet sich besonders bei der Untersuchung von elektronischen Geräten an, da hier der zufällige Fehler überwiegt und sich konstant über die Zeit verhält.
Die Einheit für die Ausfallrate ist FIT, dies ist ein Akronym und steht für Failure In Time, wobei 1 FIT für einen Ausfall pro 109 Stunden.
Die bestimmung der Ausfallrate wird wie in den folgenden Abschnitten näher erläutert.
1.2.1 Zuverlässigkeitsanalyse bei konstanter Fehlerrate
Die Konstante Fehlerrate über eine Grundgesamtheit lässt sich durch die Division der im Beobachtungszeitraum Ausgefallenen Komponenten zur Gesamtzahl ermitteln.
Konstante Fehlerrate der Grundgesamtheit
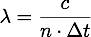
Hierbei beziehen sich die Parameter auf die Grundgesamtheit und werden wie folgt definiert:

Aus der vorangegangenen Definition lässt sich folgender Schätzer entwickeln der die Fehlerrate für eine Stichprobe bestimmt.
Schätzer der konstanten Fehlerrate
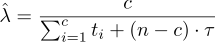
Hierbei beziehen sich die Parameter auf eine Stichprobe und werden
wie folgt definiert:
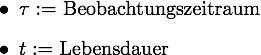
Des Weiteren lässt sich bei einer konstanten Fehlerrate folgern, dass die Dichtefunktion der Ausfallwahrscheinlichkeit eine Exponentialfunktion der nachfolgenen Form ist.
Ausfalldichtefunktion bei konstanter Fehlerrate
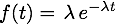
Daraus lässt sich durch Integration die Vertilungsfunktion der Ausfallwahrscheinlichkeit und die Überlebensfunktion bilden.
Verteilungsfunktion
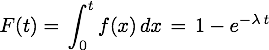
Überlebensfunktion

Eine weitere wichtige Kenngöße ist die mittlere Dauer bis zum eintreten des Ausfalls die in den einschlägigen Normen und Literatur oft nur unter MTTF (Mean-Time-To-Failure) vorzufinden ist. Hierbei handelt es sich im Fall der Exponentialverteilung um den Erwartungswert der Zufallsvariablen T.
MTTF - mittlere Dauer bis zum Eintreten des Ausfalls
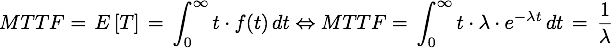
1.2.2 Zuverlässigkeitsanalyse bei variabler Fehlerrate
Die konstante Fehlerrate spiegelt natürlich nur das grundsätzliche verhalten als Mittelwert wieder. Für elektronische Komponenten und Sytmen beschriebt dies zwar eine gute annäherung, jedoch ist bei einer vielzahl von Systemen mit einer variablen Fehlerrate über die Zeit zu rechnen. Als anschauliches Beispiel kann hier der Mensch dienen. Ein Mensch ob Mann oder Frau wird zwar in einem gewissen Maße zufällig "ausfallen", trotz allem überwiegt jedoch das friedliche alterungsbedingte Dahinscheiden.
Daher wird zur gernerellen analyse ein Modell mit variabler Ausfallrate gesucht, das sozusagen die Vorgeschichte der untersuchten Komponenten ebenfalls berücksichtigt. In der Chronik der Zuverlässigkeitsanalyse kistallisierte sich die Weibullverteilung für diesen Verwendungszweck heraus. Bennant und für diesen Einsatzzweck entdeckt wurde diese von dem schwedischen Ingenieur und Mathematiker Waloddi Weibull um 1951.
Die Funktion wird mittels zweier Parameter beschrieben. Dies sind zum einen der Skalenparamerte 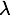 und zum anderen der Formparameter
und zum anderen der Formparameter 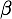 .
.
Im praktischen Umfled kann der Formparameter im Bereich 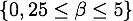 gefunden werden.
gefunden werden.
Des Weiteren lässt sich die Weibullverteilung durch eine geschickte Wahl von 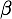 in andere Wahrscheinlichkeitsverteilungen überführen:
in andere Wahrscheinlichkeitsverteilungen überführen:

Wobei für alle nachfolgenden Definitoinen folgender Definitionsbereich gilt:
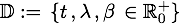
Dichtefunktion
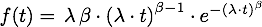
Verteilungsfunktion
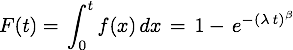
Überlebensfunktion
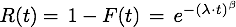
Ausfallraten-/Hazardfunktion
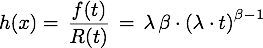
Erwartungswert}
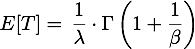
Kommt man nun auf die im Eingang des Kapitels aufgefühten Fehlertypen zurück, so können diese bei entsprechnder Wahl von 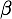 mittels der Weibull-Funktionenen abgebildet werden:
mittels der Weibull-Funktionenen abgebildet werden:

1.2.3 Generelle Initialisierung, Bibliothekimportierung und Konfiguration
#Magics
% matplotlib notebook
#% matplotlib inline
#Pakete und Module
from matplotlib import pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from mpl_toolkits.mplot3d import Axes3D
from cycler import cycler
import numpy as np
#Farben
th_rot ='#c81e0f'
th_orange='#ea5a00'
th_violett='#b43092'
th_grau = 'darkgray'
th_dunkel_grau= 'gray'
# Erstellen der TH-CI-Farbmap
th_cmap = LinearSegmentedColormap.from_list('',[th_rot,th_grau,th_orange,th_violett,th_dunkel_grau],128)
th_color_cycler= cycler('color', th_cmap(np.linspace(0,1,10)))
#Graph-Konfigurationen
plt.rcParams['figure.figsize'] = (8,6) # Festlegen der generrellen Plotgröße
plt.rcParams['axes.grid'] = True # Grid anzeigen
plt.rcParams['grid.linestyle'] = ':' # Festlegen der Grid-Linienart
plt.rcParams['axes.prop_cycle']= th_color_cycler # Festlegen der Plot-Farben
1.2.4 Implementierung der Familie der Weibullfunktionen
def weibfunc_in_def_area(func, t,scale,shape):
return 0.0 if t * scale * shape <= 0 else func(t,scale,shape)
_weibull_pdf = lambda t, scale, shape: scale * shape * (t * scale) ** (shape - 1) \
* np.exp(-(scale * t) ** shape)
_weibull_cdf = lambda t, scale, shape: 1- np.exp(-(scale * t) ** shape)
_weibull_survival = lambda t, scale, shape: np.exp(-(scale * t) ** shape)
_weibull_hazard = lambda t, scale, shape: scale * shape * (t * scale) ** (shape - 1)
def weibull_pdf(t,scale,shape):
return np.array([weibfunc_in_def_area(_weibull_pdf, ti,scale,shape) for ti in t])
def weibull_survival(t,scale,shape):
return np.array([weibfunc_in_def_area(_weibull_survival, ti,scale,shape) for ti in t])
def weibull_cdf(t,scale,shape):
return np.array([weibfunc_in_def_area(_weibull_cdf, ti,scale,shape) for ti in t])
def weibull_hazard(t,scale,shape):
return np.array([weibfunc_in_def_area(_weibull_hazard, ti,scale,shape) for ti in t])
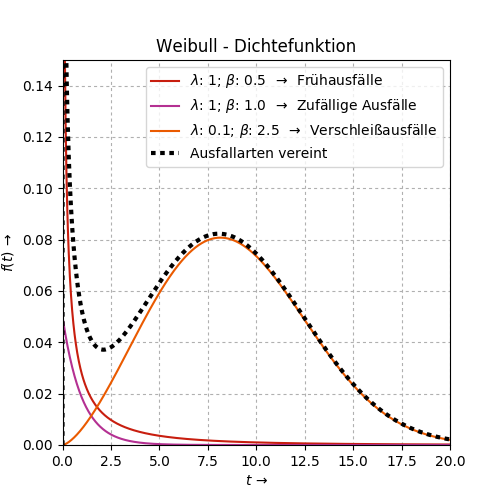
1.2.5 Plot: Weibull - Dichtefunktion
# Parameter Definition
scale = 1
scale_aged = 0.1
shape_early = 0.5
shape_rand= 1.0
shape_aged= 2.5
# Laufvariable
t = np.linspace(0,20,1000)
# Weibull-Dichtefunktion der einzelenen Ausfallarten
weibull_aged = 0.8*weibull_pdf(t,scale_aged,shape_aged)
weibull_rand = 0.05*weibull_pdf(t,scale,shape_rand)
weibull_early = 0.15*weibull_pdf(t,scale,shape_early)
# Weibull-Dichtefunktion über alle Ausfallarten
weib_pdf_union = weibull_aged + weibull_rand + weibull_early
# Erstellen der Legendebezeichnungen
label_early = r'{}: {}; {}: {} $\,\rightarrow \,$ Frühausfälle'.format(
r'$\lambda$',scale, r'$\beta$',shape_early)
label_rand = r'{}: {}; {}: {} $\,\rightarrow \,$ Zufällige Ausfälle'.format(
r'$\lambda$',scale, r'$\beta$',shape_rand)
label_aged = r'{}: {}; {}: {} $\,\rightarrow \,$ Verschleißausfälle'.format(
r'$\lambda$',scale_aged, r'$\beta$',shape_aged)
#Plotten der Funktionen
fig, ax1= plt.subplots(1,1, figsize=(5,5), sharex=True)
ax1.plot(t,weibull_early, label= label_early, color= th_rot)
ax1.plot(t,weibull_rand, label= label_rand, color= th_violett)
ax1.plot(t,weibull_aged, label= label_aged, color= th_orange)
ax1.plot(t, weib_pdf_union, label= 'Ausfallarten vereint',
color= 'k', linewidth=3, linestyle=':')
# Konfiguration des Ausgabegraphens
ax1.set_ylabel(r'$f(t) \, \rightarrow$')
ax1.set_xlabel(r'$t \, \rightarrow $')
ax1.set_title('Weibull - Dichtefunktion')
ax1.set_xlim(0,20)
ax1.set_ylim(0,.15)
ax1.legend()
# Speichern des Graphs als PDF
fig.savefig('Dichtefunktion.pdf')
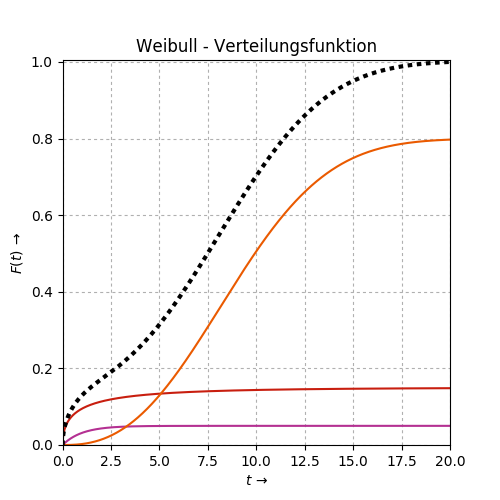
1.2.6 Plot: Weibull - Verteilungsfunktion
# Weibull-Verteilfunktion über alle Ausfallarten
weib_cdf_union = 0.15*weibull_cdf(t,scale,shape_early) \
+ 0.05*weibull_cdf(t,scale,shape_rand) \
+ 0.8*weibull_cdf(t,scale_aged,shape_aged)
weib_cdf_union /= weib_cdf_union.max()
#Plotten der Funktionen
fig, ax1= plt.subplots(1,1, figsize=(5,5), sharex=True)
ax1.plot(t,0.15*weibull_cdf(t,scale,shape_early), label= label_early, color= th_rot)
ax1.plot(t,0.05*weibull_cdf(t,scale,shape_rand), label= label_rand, color= th_violett)
ax1.plot(t,0.8*weibull_cdf(t,scale_aged,shape_aged), label= label_aged, color= th_orange)
ax1.plot(t,weib_cdf_union, label= 'Ausfallarten vereint',
color= 'k', linewidth=3, linestyle=':')
# Konfiguration des Ausgabegraphs
ax1.set_ylabel(r'$F(t) \, \rightarrow$')
ax1.set_xlabel(r'$t \, \rightarrow $')
ax1.set_title('Weibull - Verteilungsfunktion')
ax1.set_xlim(-0.005,20)
ax1.set_ylim(0,1.005)
#ax1.legend()
# Speichern des Graphs als PDF
fig.savefig('Verteilungsfunktion.pdf')
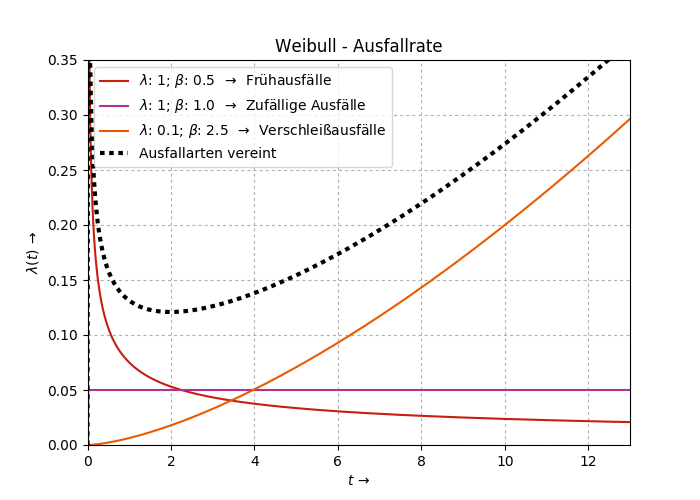
1.2.7 Plot: Weibull - Harzadfunktion
# Weibull-Harzadfunktion über alle Ausfallarten
weibull_hazard_union = 0.15*weibull_hazard(t,scale,shape_early) \
+ 0.05*weibull_hazard(t,scale,shape_rand) \
+ 0.8*weibull_hazard(t,scale_aged,shape_aged)
#Plotten der Funktionen
fig, ax1= plt.subplots(1,1, figsize=(7,5), sharex=True)
ax1.plot(t,0.15*weibull_hazard(t,scale,shape_early), label= label_early, color= th_rot)
ax1.plot(t,0.05*weibull_hazard(t,scale,shape_rand), label= label_rand, color= th_violett)
ax1.plot(t,0.8*weibull_hazard(t,scale_aged,shape_aged), label= label_aged, color= th_orange)
ax1.plot(t,weibull_hazard_union, label= 'Ausfallarten vereint',
color= 'k', linewidth=3, linestyle=':')
# Konfiguration des Ausgabegraphens
ax1.set_ylabel(r'$\lambda(t) \, \rightarrow$')
ax1.set_xlabel(r'$t \, \rightarrow $')
ax1.set_title('Weibull - Ausfallrate')
ax1.set_xlim(0,13)
ax1.set_ylim(0,.35)
ax1.legend()
# Speichern des Graphs als PDF
fig.savefig('Ausfallrate.pdf')
Congratulations @trexcoder! You received a personal award!
Happy Birthday! - You are on the Steem blockchain for 1 year!
Click here to view your Board
Congratulations @trexcoder! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!