O tema das dizimas periódicas é recorrente nos mais amplos níveis da sociedade. Desde de jovens estudantes até pessoas que já atuam no mercado de trabalho. Tendo isso em vista, resolvi abordar o assunto.
O que é uma dizima periódica?
(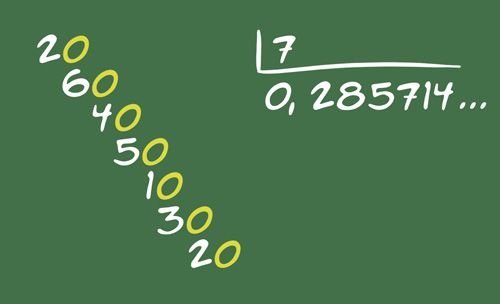 )
)
Uma dizima periódica é um número que quando escrito da forma decimal, apresenta em determinado momento a repetição de algum período.
Exemplos:
- 0,3333333333333333333333...
- 2,666666666666666666666...
- 4,999999999999999999999...
- 0,2323232323232323232323...
- 0,0005555555555555555555...
- 0,0024252425242524252425...
- 9,12345678901234567890...
- 0,5687142857142857142857...
O que é o período:
O período é a parte da dizima periódica após a virgula em que há a repetição.
Períodos dos exemplos dados de dizimas:
- 3 (1 algarismo)
- 6 (1 algarismo)
- 9 (1 algarismo)
- 23 (2 algarismos)
- 5 (1 algarismo)
- 2425 (4 algarismos)
- 1234567890 (10 algarismos)
- 142857 (6 algarismos)
O que é o antiperíodo:
O antiperíodo é a parte da dizima periódica após a virgula em que não há a repetição.
Antiperíodos dos exemplos dados de dizimas:
- 000
- 00
- 5687
Existem dois tipos de dizimas periódicas:
- Simples: o período vem logo após a virgula. Exemplos: 0,3333333... e 0,67676767...
- Composta: o período não vem logo após a virgula. Exemplos: 0,005555... e 0,0121212...
Como transformar uma dizima periódica em fração?
Primeiramente devemos sempre que possível, separar a parte inteira e a parte decimal do número. Possibilitando assim, cálculos mais simples. Após isso, devemos observar se a dizima é simples ou composta;Dizimas simples:
Dizimas como 0,121212... , 7,2222... , são bem fáceis de resolver. Para transformá-las em fração, deve-se utilizar o período como numerador da fração e o denominador será formado pelo dígito 9. O que determina a quantidade de dígitos 9 que serão utilizados é a quantidade de algarismos do período. Exemplos:
- 0,121212... Temos uma dizima simples, portanto podemos utilizar o método dado. O período é 12 e tem 2 algarismos. Portanto a fração será: 12/99
- 7,2222... Pode-se escrever esse numero da seguinte forma 7 + 0,2222... . 0,2222... tem período 2 e tem 1 algarismo. Portanto 0,2222... = 2/9. O número 7 pode ser escrito da forma 63/9, sendo assim, temos que 7 + 2/9 = 63/9 + 2/9 = 65/9
Dizimas compostas:
Dizimas como 0,00055555... e 0,0324252425... , já são um pouco mais trabalhosas. Para transformá-las em fração teremos o numerador como o (antiperíodo seguido do período) - (o antiperíodo). O denominador será composto de 9s e 0s. A quantidade de 9s será a quantidade de dígitos do período e a quantidade de 0s será a quantidade de dígitos do anteperíodo. Exemplos:
- 0,00055555... . Numerador = (antiperíodo seguido do período) - (o antiperíodo) = (0005) - (000) = 5. Denominador, período tem 1 algarismo e o antiperíodo tem 3 algarismos, logo o denominador será: 9000. Portanto a fração será: 5/9000 = 1/1800
- 0,0324252425... . Numerador = (antiperíodo seguido do período) - (o antiperíodo) = (032425) - (03) = 32422. Denominador, período tem 4 algarismo e o antiperíodo tem 2 algarismos, logo o denominador será: 999900. Portanto a fração será: 32422/999900
Parabéns, seu post foi selecionado para o BraZine! Obrigado pela sua contribuição!

Eu que agradeço pela divulgação!