Image: from en.wikipedia.org (google images labeled for re-use)
Note:
This article is of the form Wikipedia Report and it is a method used to facilitate the assimilation of researched information into a working understanding which is analogous to the classic Book Report from grade school. I won't necessarily be using Wikipedia exclusively but of course it is the starting point of choice for quick research, (If you have an opinion about a better method please let me know, I am endeavoring to ingrain good researching habits & any assistance would be greatly appreciated) simply because of the sheer scope of topics covered.Merkel Tree
What is a Merkel Tree?
"In cryptography and computer science, a hash tree or Merkle tree is a tree in which every non-leaf node is labelled with the hash of the labels or values (in case of leaves) of its child nodes. Hash trees allow efficient and secure verification of the contents of large data structures. Hash trees are a generalization of hash lists and hash chains." -- from Wiki
Well then what is are these bold terms? Well...
- hash tree
In computer science, a hash tree (or hash trie) is a persistent data structure that can be used to implement sets and maps, intended to replace hash tables in purely functional programming. In its basic form, a hash tree stores the hashes of its keys, regarded as strings of bits, in a trie, with the actual keys and (optional) values stored at the trie's "final" nodes. - hash lists
In computer science, a hash list is typically a list of hashes of the data blocks in a file or set of files. Lists of hashes are used for many different purposes, such as fast table lookup (hash tables) and distributed databases (distributed hash tables). This article covers hash lists that are used to guarantee data integrity. - hash chains
A hash chain is the successive application of a cryptographic hash function to a piece of data. In computer security, a hash chain is a method to produce many one-time keys from a single key or password. For non-repudiation a hash function can be applied successively to additional pieces of data in order to record the chronology of data's existence.
So a Merkel Tree is a specific type of a more general data structure of associated data blocks and hashes. In the case of the Merkel Tree the bifurcation successive nodes is the general convention, however more than two nodes can be implemented in a specific instance; or rather the Merkel Tree is not limited to being a binary tree by virtue of the encryption method used in its structure.
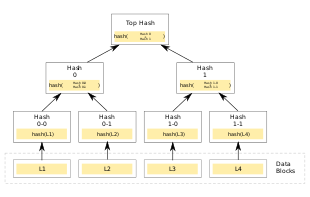
Figure 1. -- Merkel Tree
From Wiki -- -"Hash trees can be used to verify any kind of data stored, handled and transferred in and between computers. Currently the main use of hash trees is to make sure that data blocks received from other peers in a peer-to-peer network are received undamaged and unaltered, and even to check that the other peers do not lie and send fake blocks. Suggestions have been made to use hash trees in trusted computing systems"_
The use of a Merkel Tree as a data structure to ensure non-compromised and non-corrupted data transfer between computers in a Secure Development Environment is a reasonable engineering technique. At any particular point you can easily determine the immediate parent or child of a particular node. Version control could also take advantage of this architecture--The gist of it being that at any particular point in the tree, at any particular node, it knows its parent and its child, thus fake or corrupted/altered data will not be palatable to the system employing this data structure for verification.
Okay well that was informative, apparently this is part of the basis for the interesting technologies in recent years such as: Git, Bitcoin, Apache Cassandra& BitTorrent among others...
Thank you for reading this Wikipedia Report, please comment if I got something wrong... Until next time!
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://en.wikipedia.org/wiki/Merkle_tree