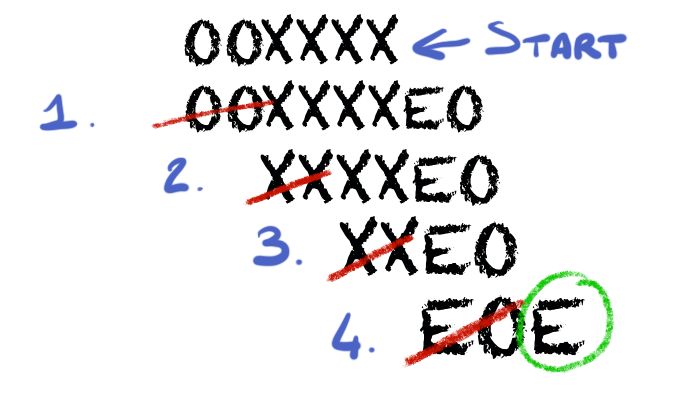
the Geniality of 2-tag systems
die Genialität von 2-Tag-Systemen
German summary below
I'd rather wanted to call that thing The Horror Of 2-Tag Systems but instead I thought people would rather like to read it if it is something smart.
See my last posts for more detailed information about that topic.
Originally I wanted to show a short and simple program which would be easily and quickly understood - even for those who are complete newbies at programming - and I failed in doing so in my last post with the bouncing ball program.
However as for yesterday I have read Minsky's Original Paper on how to emulate an UTM with a 2-tag system again and I can proof that I understood it well enough for giving a unique explanation of how 2-tag system works and how you can emulate a 2-state Turing Machine with it.
Thue is no longer of importance here but as Thue is easier to understand as a Turing Machine - I personally find it more intuitive - this post will also show how to emulate a Turing Machine in Thue.
The Sample Programm
As the bouncing ball program was to complicated and required too many states - I did not count them but just introduced states as they came handy - I thought of a shorter and simpler Programm.
Let's call it a switching number program. Let the initial string or input be 00100010, so that in order for having a simple program there should only be two symbols either 0 or 1 be allowed on the tape. Remember tape is something from the Turing Machine.
I think it's time to show the switching number program.
The Switching Number Program For The Turing Machine
input on tape : 00100010
program
;@ is the original or first state of the Turing Machine
;state symbolOnTape symbolToWrite MoveRightOrLeft newState
@ 0 0 R @
@ 1 1 R W
W 0 1 R W
W 1 1 R @
output: 00111110
The Switching Number Program in Thue
Well, it turned out the same program in Thue is actually quite the same as the program for the Turing machine. The only striking difference is that the state has to be on the tape. Thus the input has to be slightly different and that @ and W are the symbols for the two states becomes a bit more obvious.
input : @00100010
program
@0::=0@
@1::=1W
W0::=1W
W1::=1@
output: 00111110@
And now the Switching Number Program for a 2-tag system
The greatest trouble we are probably facing with 2-tag systems is that like in Thue we have to put the state on the tape but we just can read on symbol at one time while Thue allows as to read as many symbols as we want.
Thus we that one symbol has to include state and symbol to be read which means that we need a lot more symbols than in the other two programs.
It turned out after a lot of trying and failing that an equivalent program for a 2-tag system needs at least five symbols.
0 is 0 when read in state @
1 is 1 when read in state 1
i is 1 when read in state W
o is 0 when read in state W
+ is just used to trigger a new state or switch between states
It turns out that it is necessary to quite radically modify the input string. To every symbol read in state @ we add how it would look like in state W. (...sure, that could be said a bit better or left out entirely)
Here's the input string for the 2-tag system: 0o0o1i0o0o0o1i0o
program
0->0o
o->i1
1->i1+
i->i1
+->
The last line ( +-> ) means that when the symbol + is read there is nothing added and thus just + and another symbol is erased.
one of the cycles is actually : 0o0oi1i1i1i1i1+0o
The problem with the 2-tag program is that unlike the Turing nor the Thue program the 2-tag program does not halt. However one of the 'outputs' are equivalent to the other two programs.
And now the modified version of the program
Actually I could not sleep well with the old 2-tag system being posted as the program does ruin the correct output and does not terminate. So yesterday after filling again sheets of paper with my thoughts and drawings I came up with a modification. The new program uses a blocker symbol '-' and the + disappeared.
As the triggering to new states is done by odd numbers and two odd numbers sum up to an even number, this can be used in the same way a simple button can work as an on/off-switch.
Here's the new input for the program : 0o0o-i10o0o0o-i10o
program
0->0o
o->i1
i->i1
-->i1
1->
the repeating output after 8 'cycles': 0o0oi1i1i1i1i10o
The programming reaches the repeating output after 11 'cycles'.
Finally here's a summary of my desperation with a picture in one of the many sheets of paper I used for thinking that out.

Zusammenfassung
Wie seit den 60er Jahren durch Minsky bekannt lässt sich eine Turing-Maschine mit zwei Zuständen durch ein 2-Tag-System emulieren. Der Artikel von Minsky wurde zigfach zitiert und führte zu relativ einfachen und minimalen Turingmaschinen in den 90ern. Z.B. bezieht sich Rogozhin auf Minsky's Artikel wie er seine UTM(2,18) vorstellt.
Da ein 2-Tag-System den internen Zustand nicht speichern kann und lediglich ein Symbol pro Takt lesen kann, muss die Eingabe oder der Input modifiziert werden. Der entscheidende Schmäh oder Trick dabei ist, dass bei einem 2-Tag-System das zweite Symbol gelöscht wird ohne gelesen zu werden. Indem man mal drei Symbol statt zwei Symbole anhängt kann man so mit Hilfe eines Triggersymbols in einen anderen Zustand wechseln.
Ich kenn nur
ein- 2 Kaffee Tag-System oder
!COFFEEA 3
System
das triggert auch um in einen
anderen Zustand zu wechseln.
Bahnhof
Ja, nachdem mans händisch selbst auf Papier zigmal durchlaufen hat oder besser ein Programm geschrieben hat, was das für einen macht, dann wird das ganze schon um einiges klarer. Im Grunde bestehen alle drei "Systeme" aus Ersetzungsregeln. Der Unterschied bei einem Tag-System ist lediglich, dass man nur ein Symbol durch nichts oder mehrere "ersetzen" - also in dem Fall anhängen kann. Das erste Bild erklärt bis auf die Regeln recht schön wie ein 2-Tag-System funktioniert. Konstruierte Haltebedingung ist dass es keine zwei Symbole mehr zum Löschen oder Wegstreichen gibt.
Noch ein Versuch
!COFFEEA
Hallo ich bin Mikrobi,
dein Beitrag hat mir sehr gut gefallen und du bekommst von mir Upvote.
Ich bin ein Testbot, wenn ich alles richtig gemacht habe, findest du deinen Beitrag in meinem Report wieder.
LG
Mikrobi