0.0 Setup
This guide was written in Python 3.6.
0.1 Python and Pip
0.2 Libraries
We'll be working with numpy and scipy, so make sure to install them. Pull up your terminal and insert the following:
pip3 install scipy==0.19.0
pip3 install numpy==1.12.1
1.0 Introduction
Linear Algebra is a branch of mathematics that allows you to concisely describe coordinates and interactions of planes in higher dimensions, as well as perform operations on them.
Think of it as an extension of algebra into an arbitrary number of dimensions. Linear Algebra is about working on linear systems of equations. Rather than working with scalars, we work with matrices and vectors. This is particularly import to the study of computer science because vectors and matrices can be used to represent data of all forms - images, text, and of course, numerical values.
1.1 Why Learn Linear Algebra?
Machine Learning: A lot of Machine Learning concepts are tied to linear algebra concepts. Some basic examples, PCA - eigenvalue, regression - matrix multiplication. As most ML techniques deal with high dimensional data, they are often times represented as matrices.
Mathematical Modeling: for example, if you want to capture behaviors (sales, engagement, etc.) in a mathematical model, you can use matrices to breakdown the samples into their own subgroups. This requires some basic matrix manipulation, such as atrix inversion, derivation, solving partial differential, or first order differential equations with matrices, for example.
1.2 Scalars & Vectors
You'll see the terms scalar and vector throughout this course, so it's very important that we learn how to distinguish between the two. A scalar refers to the magnitude of an object. In contrast, a vector has both a magnitude and a direction.
An intuitive example is with respect to distance. If you drive 50 miles north, then the scalar value is 50. Now, the vector that would represent this could be something like (50, N) which indicates to us both the direction and the magnitude.
1.3 Importance
There are many reasons why the mathematics of Machine Learning is important and I’ll highlight some of them below:
Selecting the right algorithm which includes giving considerations to accuracy, training time, model complexity, number of parameters and number of features.
Choosing parameter settings and validation strategies.
Identifying underfitting and overfitting by understanding the Bias-Variance tradeoff.
Estimating the right confidence interval and uncertainty.
1.4 Notation
∈ refers to "element in". For example 2 ∈ [1,2,3,4]
ℜ refers to the set of all real numbers.
1.5 Challenge
Using the distance formula and trigonometry functions in Python, calculate the magnitude and direction of a line with the two coordinates, (5,3) and (1,1).
For more information on distance formula and trigonometry functions
2.0 Vectors
As we mentioned in the previous section, a vector is typically an ordered tuple of numbers which have both a magnitude and direction. It's important to note that vectors are an element of a vector space.
In the next section, we'll learn about matrices, which are a rectangular array of values. A vector is simply a one dimensional matrix.
Sometimes what we're given, however, isn't a neat two value tuple consisting of a magnitude and direction value. Sometimes we're given something that resembles a list, and from there, we can create a tuple that describes the vector.
With that said, we can represent a vector with a list, for example:
A = [2.0, 3.0, 5.0]
From this vector we can then calculate the magnitude as we've done before:
nln.norm(A)
Getting us a value of approximately 6.16. In many instances, vectors are also made with numpy arrays.
import numpy as np
A = np.array([2.0, 3.0, 4.0])
2.0.1 Challenge
Write code for two vectors with five values of your choice. The first should be written as a regular one-dimensional list. The other should be be written with numpy.
If we call the method norm() on this array, we get the same value, 6.16.
2.1 What is a vector space?
A vector space V is a set that contains all linear combinations of its elements. In other words, if you have a set A, the space vector V includes all combinations of the elements in A.
With that said, there are three properties that every vector space must follow:
Additive Closure: If vectors u and v ∈ V, then u + v ∈ V
When we earlier stated that the vector space has all combinations of the elements in set A, one of the operations we meant by 'combinations' was vector addition. For example if we have two vectors in set A, let's say (4, 5) and (3, 1), then the vector space of A must have those two vectors, as well as the vector (4+3, 5+1), or(7, 6). This has to be true for any two vectors in set A.Scalar Closure: If u ∈ V, then α · u must ∈ Ν for any scalar α
Recall that a scalar is a magnitude value with no direction, such as 5. For a vector space to be a vector space, that means for every vector in the original set A, that vector multiplied by any number (or constant or scalar) must be in the vector space V.Additive Identity: There exists a · 0 ∈ V such that u + 0 = u for any u ∈ V
In other words, the vector space of set A must contain the zero vector.Additive Associativity: If u, v, w ∈ V, then u + (v + w) = (u + v) + w
Regardless of the order in which you add multiple vectors, their results should be the sameAdditive Inverse: If u ∈ V, then there exists a vector −u ∈ V so that u + (−u) = 0.
For example, if the vector (2, 3) ∈ V, then its additive inverse is (-2, -3) and must also be an element of the vector space V.
The dimension of a vector space V is the cardinality. It's usually denoted as superscript, for example, ℜn. Let's break down what this looks like:
ℜ2 refers to your typical x, y systems of equations.
ℜ3 adds an extra dimension, which means adding another variable, perhaps z.
2.2 What is a subspace?
A vector subspace is a subset of a vector space. That subspace is also a vector space, so it follows all the rules we reviewed above. It's also important to note that if W is a linear subspace of V, then the dimension of W must be ≤ the dimension of V.
The easiest way to check whether it's a vector subspace is to check if it's closed under addition and scalar multiplication. Let's go over an example:
Let's show that the set V = {(x, y, z) | x, y, z ∈ ℜ and xx = zz } is not a subspace of ℜ3.
If V is actually a subspace of ℜ3, that means it must follow all the properties listed in the beginning of this section. Recall that this is because all subspaces must also be vector spaces.
Let's evaluate the first property that stays the following:
If vectors u and v ∈ V, then u + v ∈ V
Now, is this true of the set we've defined above? Absolutely not. (1, 1, 1) and (1, 1, -1) are both in V, but what about their sum, (1, 2, 0)? It's not! And because it's not, it does not follow the required properties of a vector space. Therefore, we can conluse that it's also not a subspace.
2.2.1 Challenge
Write the representation of ℜ2 as a list comprehension - use ranges between -10 and 10 for all values of x and y.
Write the representation of ℜ3 as a list comprehension - use ranges between -10 and 10 for all values of x, y, and z.
Write a list comprehension that represents the the set V = {(x, y, z) | x, y, z ∈ ℜ and x+y = 11}. Use ranges between -10 and 10 for all values of x, y, and z.
Choose three values of x, y, and z that show the set V = {(x, y, z) | x, y, z ∈ ℜ and x+y = 11} is not a subspace of ℜ3. These values should represent a tuple that would be in vector V had it been a vector subspace. Each value should also be between -10 and 10.
2.3 What is Linear Dependence?
A set of vectors {v1,...,vn} is linearly independent if there are scalars c1...cn (which aren't all 0) such that the following is true:
c1v1 + ... + cnvn = 0
2.3.1 Example
Let's say we have three vectors in a set: x1 = (1, 1, 1), x2 = (1, -1, 2), and x3 = (3, 1, 4).
These set of vectors are linear dependent because 2x1 + x2 - x3 = 0. Why is this equal to zero? Again, because 2*(1,1,1) + 1(1,-1,2) - (3,1,4) = (2+1-3, 2-1-1, 2+2-4) = (0, 0, 0). If we can find some equation that satisfies a resultant of 0, it's considered linear dependent!
2.3.2 What is Linear Independence?
A set of vectors is considered linear dependent simply if they are not linear dependent! In other words, all the constants from the previous section should be equal to zero. c1 = c2 = ... = cn = 0
2.4 What is a basis?
Any linearly independent set of n vectors spans an n-dimensional space. This set of vectors is referred to as the basis of ℜn.
2.4.1 Under vs Overdetermined Matrices
When m < n, the linear system is said to be underdetermined, e.g. there are fewer equations than unknowns. In this case, there are either no solutions or infinite solutions and a unique solution is not possible.
When m > n, the system may be overdetermined. In other words, there are more equations than unknowns. They system could be inconsistent, or some of the equations could be redundant.
If some of the rows of an m x n matrix are linearly dependent, then the system is reducible and we get get rid of some of the rows.
Lastly, if a matrix is square and its rows are linearly independent, the system has a unique solution and is considered invertible.
2.5 What is a Norm?
Remember the distance formula from the intro section? That's what a norm is, which is why that function we used from scipy was called linalg.norm. With that said, just to review, a norm just refers to the magnitude of a vector, and is denoted with ||u||. With numpy and scipy, we can do calculate the norm as follows:
import numpy as np
from scipy import linalg
v = np.array([1,2])
linalg.norm(v)
The actual formula looks like:
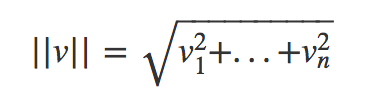
2.5.1 Challenge
Find the norm of the vector [3, 9, 5, 4] using the actual formula above. You should write a function find_norm(v1) that returns this value as a float and then call it on the provided variable n1. You should not use scipy, but you may use the math module.
Resources
Feel free to leave solutions in the comments -- I'll do my best to respond back! In case you found this topic particularly useful, I've included some wonderful resources below to continue your knowledge.