People especially newcomer or those who don't really do programming at all may find it extremely hard to understand the difference between Classic Machine learning and Deep learning and AI. A general suspicion is that Deep learning seems to be the "thing" that came up a few years ago and completely outperform human at different tasks. How does this happen? Why now?
Part of the actual code of the deep neural network developed by google Tensorflow
The term AI is, to be honest, arbitrary and hard to have a good definition (unless you are a smart business man who knows how to bullshit). But I think there is a huge distinction between Classic Machine learning and Deep learning. And if you understand this, you will have an intuitive idea of why Deep learning can kind of dominate the world in such short period of time.
Fully connected network and Linear Regression
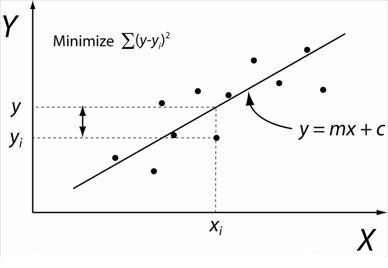
One of the practically used models in deep learning is known as Fully connected network. It's basic form can actually trace back to our classic high school math, linear regression.
Yes, the classic Y = mx + c.
so m and c are what we call parameters. For example, right now we are trying to predict the speed of a group of runners from Underwood High School by just observing their weights. Of course every high school has some slim dude and fat dude from 40kg to 130kg.
So Y = speed and x = weight
In classic machine learning, we have a "True" m and c, meaning that by mathematics manipulation, we can find the best fit m and c for this task. Although this model may not be accurate, the m and c has tried their best to predict the speed of runner.
This technique is known as "maximum likelihood" or "Minimize MSE" or "Derivative set to 0".
So right now we have 2 problems.
- The best fit line with two parameters is just not good enough. We need stronger model to fully absorb all the data-point to make a perfect prediction.
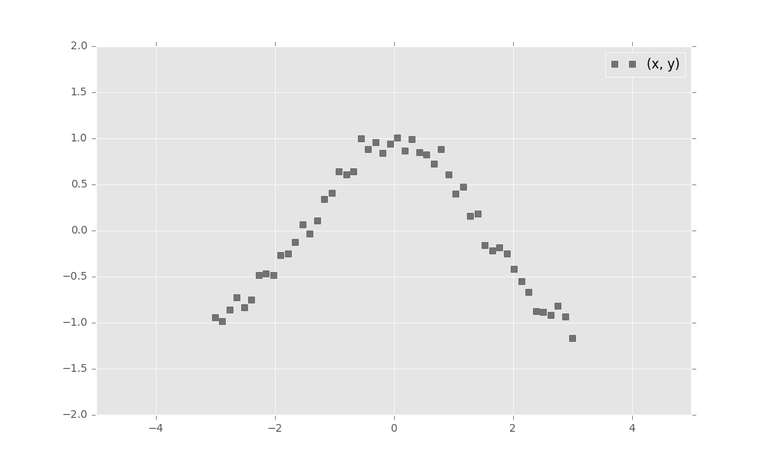
- We have another problem named 'Non-linearity'. What-if the graph of the speed of students with respect to their weight looks like this?
- If we fit a best fit linear regression line, it will look like this
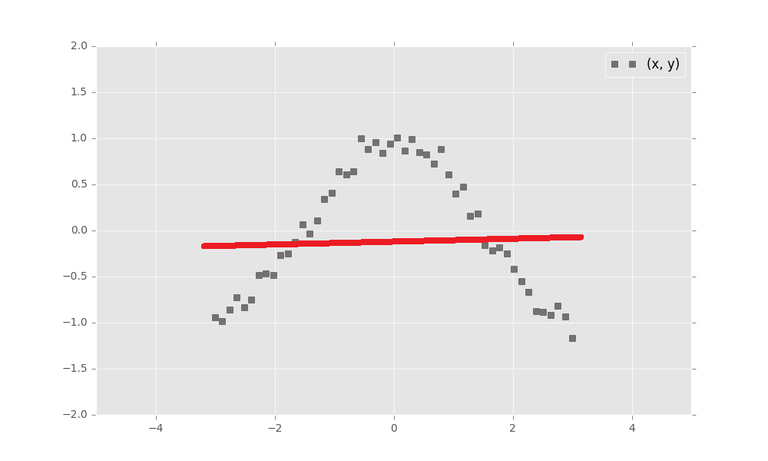
- This is what we call: Problem of non-linearity. Of course, if you think carefully, the student who perform the best in running contest should be not too fat and not too slim.
For years, researchers in top-tier university has tried to tackle the problem of non-linearity. The result was actually fine. For example, the first generation of Xbox Kinect (with games like Just-dance) was using Classic Machine learning but not deep learning to detect human body movement.
But the power of deep learning is just way better. (at least for now it is)
1. Ensemble of many linear regressions
We get back to the speed problems. What if we only use linear regression, but this time we fit 3 linear regression models in this problem?
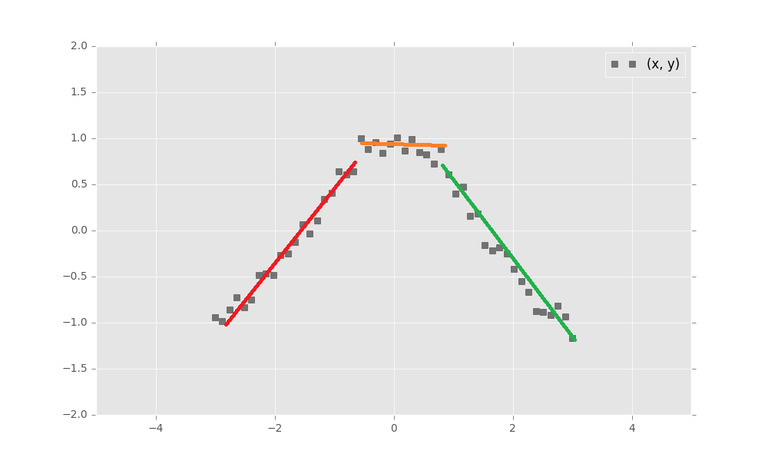
Deep learning in its basic form does exactly the same thing. In my previous project, I fit nearly 8000 linear regression lines to fully connected network. This kind of aggressive structure can help us to create a function for every problem, at least in theory.
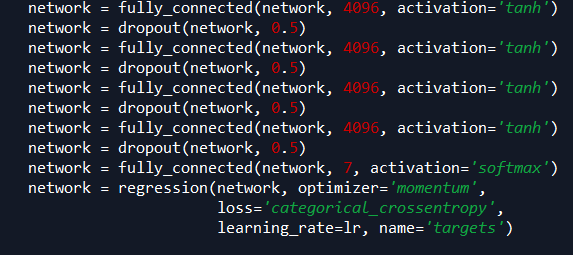
2. Activation function
The second breakthought is known as activation function. For every linear regression we will add a sigmoid function to it.
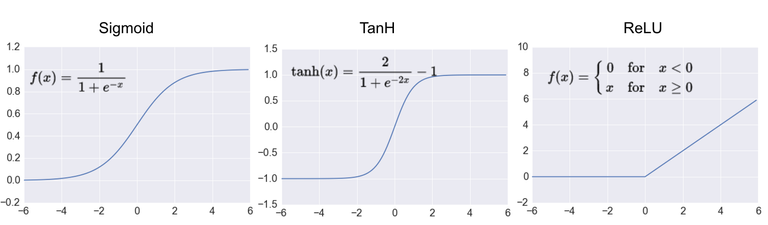
The linear line, as you can see, become non-linear immediately. This is computationally convenient and save a lot of time. As you can tell, we have a lot of linear regression needs to be trained.
The power of handling complicated task and the perfect solution in non-linearity make deep learning so strong. Imagine if we add 10000000000 linaer regressions to play chess like Alpha-Go, we can easily outperform human. (Of course this is not how Google Deep mind designs Alpha-Go, but the concept remains the same)
This post received a 2.4% upvote from @randowhale thanks to @jimsparkle! For more information, click here!
Great post! Let me mark it first and study later!
@jimsparkle, pls continue your great posts! Thanks a lot.
I scared of reading long English paragraphs and calculating. But I support you.
That was an interesting read. Glad that Tensorflow was mentioned, although I haven't played around with it much yet.
Great 101 lesson for people like me! Ready to learn more!