
PROBABILITY was initially called and for a quite a long time the doctrine of chances and was the mathematical description of game of chance (dice, cards and so on) and used to describe and quantify randomness or aleatory of uncertainty. Statisticians use it to describe uncertainty.
In 1763, a certain Thomas Bayes tried to answer the following questions:

How can you use probability to describe learning ? How can you use it to describe an accumulation of information overtime so yo can modify probability, based on additional knowledge ?
The answer was the Bayes theorem:
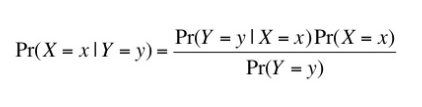
which is the probability that event x occurs given that event y occurs.
However, using Bayes theorem is a thing and being Bayesian is something else. As strange as it sounds, Thomas Bayes was not necessarily Baysian as he apparently did not really apply his theorem to REAL WORLD PROBLEMS but anyway, his invention was ingenious and worked for probability no matter what your interpretation for probability is. But Bayesians took it to the next level and used Bayes theorem to perform INFERENCES and started calculating the conditional distribution of the parameter ɵ given the observed data x, using a couple of pieces called:
LIKELIHOOD: probability density OR mass function ;
and PRIOR DISTRIBUTION: unconditional distribution that you put on the parameter ɵ (without necessarily thinking data is random).
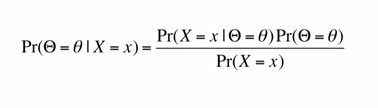
which is the probability that the distribution parameter is ɵ given that we have observed data x.
Using probability to find something that is not random is called SUBJECTIVE PROBABILITY which is a state of believe or state of knowledge. All these put together make the POSTERIOR DISTRIBUTION of ɵ given x, and of course not forgetting the constant of integration (the denominator of the formula mentioned above) as probability has always to integrate to one. And the term subjective here does not mean arbitrary or non-rigorous, it means dependent on human judgment. Everything we do inside depends on human judgement: how the experiment will be setup, choice of the prior & likelihood, …
And it s actually Pierre-Simon de Laplace (18th Centry), a "Probability Enthusiast" mathematician, who brought this change to the Bayse theorem saying that subjective probability based inference should be done to solve SCIENTIFIC PROBLEMS.
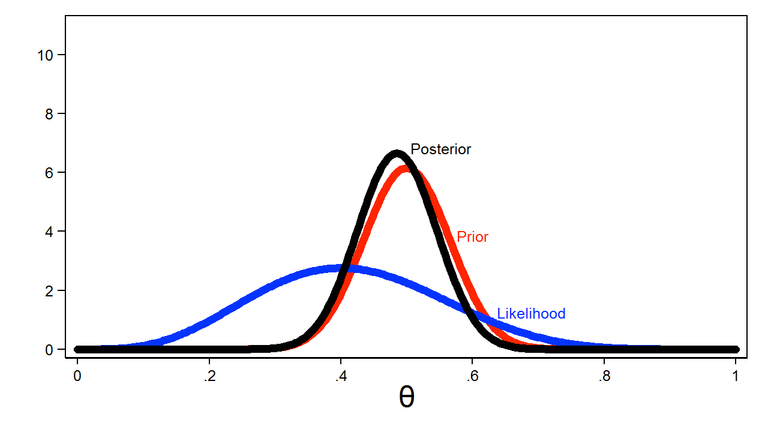
A past experience within an academic institution, showed me that the use a randomized controlled experiment to establish in a quite mathematically rigorous way (frequentist method) a causality between ALZHEIMER DISEASE and bunch of environmental & risk factors based on observational studies required not only the observation of the weight of evidences but also the use of human judgement to say, for instance, Aluminum may cause Alzheimer and not the other way around.
" The only kind of uncertainty was the uncertainty to do ignorance "
And de Laplace believed that the world was both DETERMINISTIC & PREDICTABLE and that if we had enough knowledge of starting conditions we could build quite reliable models that make good predictions. To him the only kind of uncertainty was the uncertainty to do ignorance, the kind of uncertainty you describe with subjective probability. The problem was first to come up with a good prior and second if different people come up with different priors particularly if there is not a lot of data, you can get different answers, hence the real push, back then, to get the prior out of statistics and the only way that you can do is to use inference which tied only to objective probability and randomness. That what some mathematicians who founded FREQUENTIST INFERENCE precisely did. They came up with a new way of doing statistics which is tied only to randomness and does not have subjective probability at all.
Therefore, for a given case study / experiment, we can either opt for a:
- Bayesian solution: picking a prior, calculating a posterior (posterior density), finding the 5th percentile and see the outcome with 95% subjective probability that Pr(X=1).
☞ Determining a probability distribution
- or Frequentist solution: figuring out within a confidence interval (95% of coverage probability) what outcomes of our hypothetical experience are as / more consistent with all results and identifying all Pr(X=1) that have >5% chances of producing theses same results.
☞ Calculating a probability.
Both approaches give Pr(X=1) quite close results with 5% uncertainty.
Besides, in frequentist procedures it’s very hard to understand when probability comes into play, you have this coverage probability in the confidence interval that when you are doing a hypothesis test you do not actually have the probability that the hypothesis is true. Bayesian inference can give you that because the hypothesis and the parameter value is not random, which is one of the primary Bayesian critics of Frequentist inference.
OBJECTIVE PROBABILITY is restrictive but results mean the same thing to EVERYONE. It inflexible and require ancillary randomized experiments before you can calculate results.
However, for Bayesian inference there are 2 prior related issues:
1- How to come up with a prior that really represents your believes ?
2- How to deal with different answers while using different priors ?
The solution is a concept called EXPERT ELICITATION that consist in pairing up someone who knows about probability and someone who knows about science and find a way to write a state of knowledge of science using probability.
That being said, you cannot arbitrarily combine a prior distribution with a likelihood and expect to be able to compute with it, and Bayesian inference for long time was limited to this very small family of priors & likelihood that was comparable & computable.
HOW BAYESIAN PROBABILITY IS IMPORTANT FOR THIS AI GOLD RUSH ?
There is very little that we can know for sure and most of the time we have to settle for what is most likely. Probability theory is therefore the framework of choice for dealing with uncertainty in AI.

Bayesian statistics is not new and is hundreds of years old and even older than its most popular competitors but with the fast increase in computing power reasons we have started hearing about it until fairly recently.
Few decades ago AI programs were implemented using logic where each proposition & inference was either TRUE or FALSE but the need to represent uncertainty and draw inferences from partial information arose quickly. This has reduced but not eliminated the brittleness issue in AI systems.
However, in early 90s with the Markov Chain of Monte-Carlo (MCMC), the extraordinarily powerful tool for sampling from & computing expectations with respect of a very complicated highly dimensional probability distribution, things have changed dramatically. Indeed, MCMC algorithms caused the Bayesian renaissance & enabled the sampling from a distribution even if you do not know the constant of integration which means that Bayesians now can put together any prior or likelihood they want, sample and do inference on these samples of the population. The combination of the availability of these algorithms with the availability of increasingly sophisticated computing hardware made everything possible.
As a conclusion, I will say like so many things in AI research & its applications, may be probability, too, will prove to be a red herring but in the meantime it is very useful to solve a lot of real world problems and it has now become even more popular because of the success of MACHINE LEARNING technology but that's another story...
Source: DataSkimm a Tesla Duo Group division.
Thank you for reading my post & would love to hear your thoughts on this topic.
Isaad Sainkoudje
CEO | "Consigliere" | Data Scientist | Blockchain & AI Enthusiast | Pharmacist | Philanthropreneur | Martial Artist
Bayes filter derived from Bayes theorem is currently the underlying, behind-the-scene mathematical tool used in automated driving and object tracking.