History of the Lobachevskian Geometry is a history of attempts to prove Euclid's fifth postulate. This postulate is one of the basic Euclid axioms of geometry. The fifth postulate - the last and the most difficult assumption included by Euclid in his axiomatics of geometry.

I want to recall its description to you: if two lines are intersected by the third in such a way that on any side of it the sum of the interior angles is less than two right angles, then straight lines intersect on this side.
But I need to say that if line CB considered equal to 1 m, and the angle is different from the right angle on one arc second, it can be calculated that the lines will intersect at a distance of over 200 km from the straight line - so it is really difficult to verify this experiment.
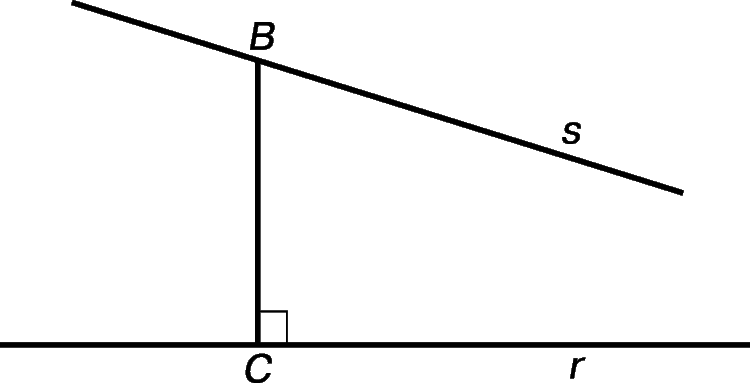
Many mathematicians, who lived after Euclid, tried to prove that this axiom is excess - can be proved as a theorem on the basis of the other axioms, but everyone failed.
And only in XIX century the professor of Kazan University Lobachevsky solved this puzzle. He tried to deduce different consequences based on the denial of the fifth postulate, hoping that sooner or later it will come to a contradiction. However, he proved many tens of theorems, without revealing logical contradictions. And then he guessed that the geometry in which the fifth postulate is replaced by its negation is not contradictory. Lobachevsky named this geometry as imaginary.
Lobachevskian Geometry retains all the theorems of Euclidean geometry which can be proved without using the fifth postulate. However, the theorems, which use parallel axiom are modified.
- For example, the theorem about the sum of the angles of a triangle - in the geometry of Lobachevsky the sum of the angles of any triangle is less than 180 °.

- If the two corners of the one triangle are respectively equal to two other corners of the other triangle, then in the Euclidean geometry the third angles are equal (triangles are similar).
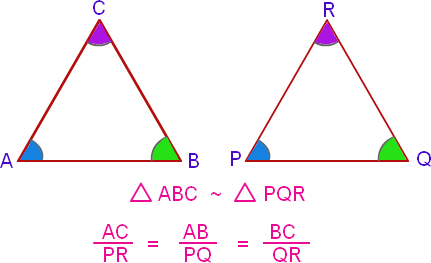
In Lobachevskian Geometry, there are no similar triangles. Moreover, there is the fourth sign of equality of triangles - if the corners of one triangle are respectively equal to the corners of the other triangle, these triangles are equal.
- The difference between 180 ° and the sum of the angles of a triangle
 in the Lobachevskii geometry is positive; it is called the defect of the triangle. It turns out that the area of a triangle in this geometry is connected with its defective:
in the Lobachevskii geometry is positive; it is called the defect of the triangle. It turns out that the area of a triangle in this geometry is connected with its defective: 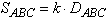 where S and D represent the area of the triangle and the defect, and k depends on the choice of unit of measurement of areas and angles.
where S and D represent the area of the triangle and the defect, and k depends on the choice of unit of measurement of areas and angles.

- Suppose now AOB – is some acute angle. In the geometry of Lobachevsky you can choose such point M on the side OB that MQ perpendicular to the side OB that does not intersect with the other side of the angle. This fact is a proof that the fifth postulate is not fulfilled: the sum of the angles is less than the straight angle, but lines OA and MQ do not intersect.

If you start moving point M to point O, then there will be such "critical" point M0, where perpendicular M0Q0 to the OB side that still does not intersect OA, but for any point M' lying between O and M0 corresponding perpendicular intersects with the OA. Lines OA and M0Q0 still get closer to each other, but do not have common points.
To obtain such a proof that his idea is not contradictory, it was necessary to build a model, but Lobachevsky himself couldn’t do it. So this work was done by the mathematicians of the next generation.
In 1868, Italian mathematician Beltrami studied the concave surface that is called a pseudosphere, and proved that the geometry of Lobachevsky is workable on this surface!
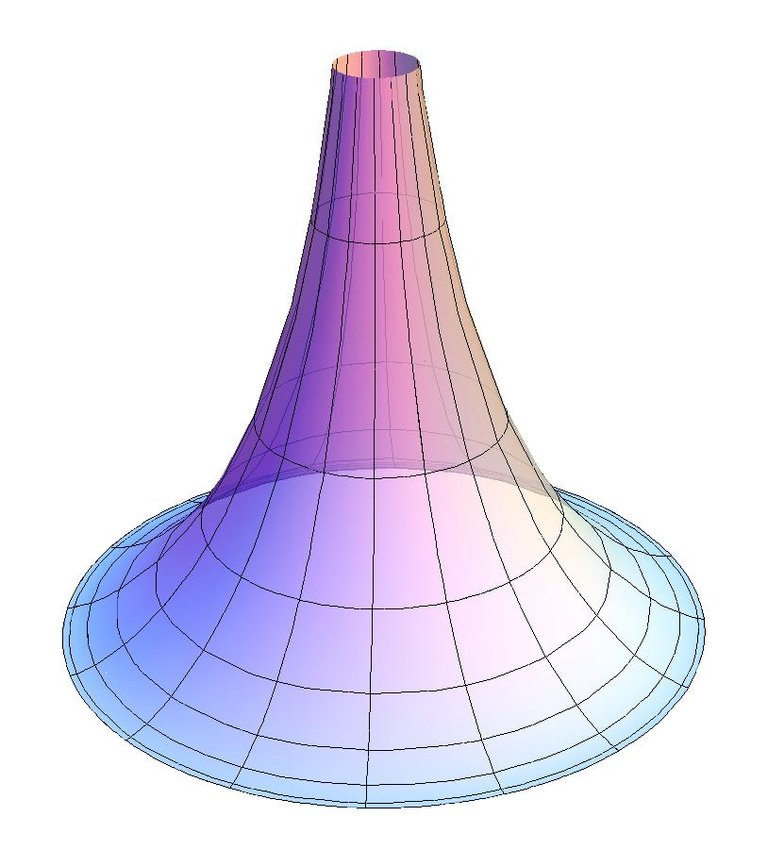
If you draw the shortest lines on this surface and measure the distance with this lines, make from the arcs of these lines triangles, etc., then it occurs that all the formulas of Lobachevskian Geometry could be implemented (in particular, the sum of the angles of any triangle is less than 180 °).
Two years later, the German mathematician Felix Klein offered another model of the Lobachevskii plane.
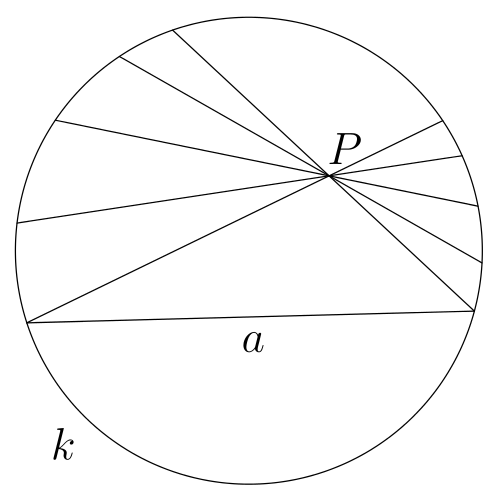
Further testing has shown that all the other axioms of Lobachevskian Geometry could be implemented on the Klein model. In particular, for any "line" (the chord of a circle) and for any point of this "line" there is a "movement" that takes it to another line with a marked point on it.
Subsequently there were other models of Lobachevskii geometry. These models finally established that Lobachevskian Geometry is not contradictory. Thus, it was shown that the Euclidean geometry is not the only possible. This had a great progressive impact on all further development of geometry and mathematics in general.
And in the XX century it was discovered that Lobachevskian Geometry is not only important for abstract mathematics as one of the possible geometries, but also directly related to the applications of mathematics in physics. It was found that the relationship of space and time, described in the special theory of relativity, is directly related to the geometry of Lobachevsky. For example, formulas of Lobachevskian Geometry are used in developing of synchrophasotron.
Follow me, to be the first to learn about my publications devoted to popular science and educational topics
With Love,
Kate
Mind blown? No, mind bent!
yep! Non-euclidian geometry is pretty mind-blowing but extremely interesting
I didn't know anything about Lobachevsky geometry and I started to be really curious when you mentioned special relativity (I am using the latter everyday and I had never heard about Lobachevsky before).
After looking about it, the Lobachevksy geometry vocabulary can be entirely translated into the Minkowski space vocabulary, which is special relativity!
Thanks for your post, I learned something today :)
really good research and your way of explaining is simple yet efficient and correct.Love geometry
I'm happy you like reading my articles
This post has been linked to from another place on Steem.
Learn more about linkback bot v0.4. Upvote if you want the bot to continue posting linkbacks for your posts. Flag if otherwise.
Built by @ontofractal