Fundamentals of the central limit theorem and the mysterious law of large numbers
The central limit theorem (CLT) expresses the fact that a sum of many independent and identically distributed random variables will tend to be distributed normally. This theorem is very useful for understanding many aspects of the theory of probability. It also explains why in some cases in the simulation signal noise can be considered as normally distributed.
General Description of CLT
Suppose that  is an infinite sequence of completely independent and identically distributed random variables, which have an expected value and variance. They will be designated as μ and σ2.
is an infinite sequence of completely independent and identically distributed random variables, which have an expected value and variance. They will be designated as μ and σ2.
So 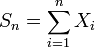 .
.
Then  by the distribution at
by the distribution at  , where N (0,1) is a normal distribution with zero expectation and a standard deviation that is equal to one.
, where N (0,1) is a normal distribution with zero expectation and a standard deviation that is equal to one.
In order to fully understand this topic, we must first pay attention to the law of large numbers, which is a special case of the CLT and is widely used in our lives.
The law of large numbers (LLN)
Practically, it can be seen that the sample results of individual observations, which are held in the same conditions, have the ability to be different, although the average result of a large number of samples will be stable and weakly depends on the results of a separate experiment. The theoretical justification of the features of random phenomena - it is the law of large numbers (LLN).

LLN claims that the empirical average (arithmetic mean) of a sufficiently large sample of a fixed distribution is close to the theoretical average (mathematical expectation) of this distribution.
But the world has long known that the arithmetic mean of numerical characteristics of certain features in a significant number of repetitions of experience is almost not subjected to deviations. If certain general conditions are met - the stability of arithmetic mean will be a certain event.
The law of large numbers in the form of Chebyshev
If the variances of independent random variables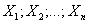 are limited only by a constant C, and they are presented in a large number, then the probability of the deviation of arithmetic mean of random variables from the arithmetic mean of their expected values is arbitrarily close to 1 and does not exceed a positive number in absolute terms, no matter how small it would be:
are limited only by a constant C, and they are presented in a large number, then the probability of the deviation of arithmetic mean of random variables from the arithmetic mean of their expected values is arbitrarily close to 1 and does not exceed a positive number in absolute terms, no matter how small it would be:
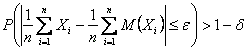
Bernoulli's theorem
Assuming that the probability of occurrence of the event A in any independent trial is constant and the number of trials is large enough, then the probability that the frequency of occurrence of an event is a little different from the probability of its occurrence is arbitrarily close to 1:
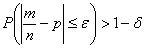
Poisson Theorem
Assuming that the probability of occurrence of an event in -th test does not change at the moment when the previous test results are known, and the number of trials is sufficiently large, then the probability that the frequency of occurrence of the event is little different from the arithmetical mean of probabilities is arbitrarily close to 1,:

In order to experimentally verify the law of large numbers different experiments were conducted.
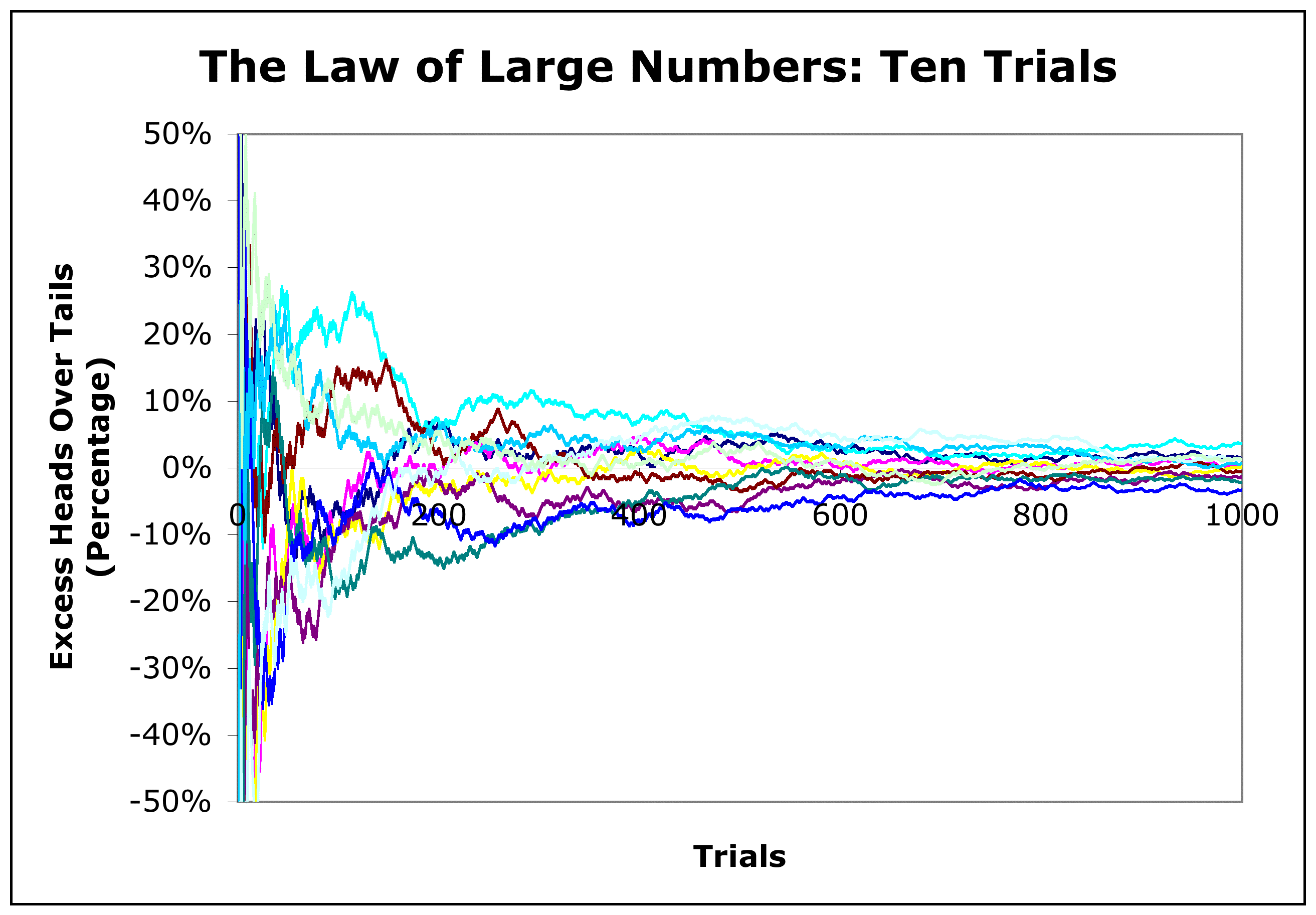
- The experiment of Buffon. The coin was flipped 4040 times. 2048 times - heads. The frequency of its loss is 0.50694
- Experiment of Pearson. Coin was flipped 12 000 and 24 000 times. And the loss rate was equal to 0.5016 and 0.5005 respectively.
- The experiment of Westergaard. From an urn with an equal number of white and black balls, 10,000 were removed one by one, returning the taken ball in the trash, 5011 white and 4989 black were picked. The frequencies of balls occurrence were, respectively, 0.50110 and 0.49890.
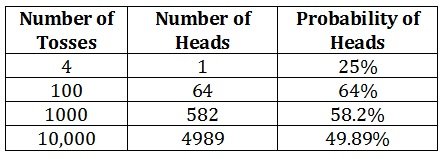
The results of these experimental tests of LLN tell us about the proximity of experienced frequency and probabilities.
LLN is included in the basis of many types of insurance, such as life insurance for various periods of time to calculate the reliability of the client.
During the allocation of consumer goods the law of large numbers is used to calculate the demand of population.
Sampling method that is used in the law of large numbers, is also used in farms in the procurement of cereal in order to determine the quality of the whole batch of grain a few cereals is taken as a sample.

The law of large numbers plays an important part in theoretical terms, as it justifies the methods of mathematical statistics. In practice, the law of large numbers can be illustrated by the example of the weather. For example, the atmospheric pressure every day is a random variable. However, its average annual value remains practically unchangeable for many years.
If you want to learn more about Central Limit Theorem I recommend to get started from these references: 1, 2
Also take a look at this video that visualizes and explains this mysterious mathematical concept
Follow me, to learn more about popular science, math and technologies
With Love,
Kate
It's cool to see math stuff here. I think Steemit could be an amazing educational source of knowledge accessible to anyone. Once I get my dull master thesis finished, I'll also post some more math related stuff. Keep it up :-)
Indeed. Steemit could be a second stackoverflow but for science and with a more engaged audience. It also encourages authors to post high-quality content that is also a good sign.
congratulations on your curie mention
Wow, thanks! Didn't know that I was mentioned in curie. Really excited